A particle starts moving in a straight line from rest with an acceleration (inm/s2) given by : a=12√x, where x is the distance travelled by the particle (in meters ) The velocity of the particle at the instant when its acceleration is 48m/s2 is .......m/s
The correct Answer is:B, C
To solve the problem, we need to find the velocity of a particle at the moment when its acceleration is 48 m/s², given that its acceleration is defined as a=12√x, where x is the distance traveled by the particle in meters.
1. Set Up the Equation for Acceleration:
We are given the acceleration as:
a=12√x
2. Substitute the Given Acceleration:
We need to find the distance x when the acceleration a is 48 m/s². Set the equation equal to 48:
12√x=48
3. Solve for √x:
Divide both sides by 12:
√x=4812=4
4. Square Both Sides to Find x:
x=42=16 m
5. Relate Acceleration to Velocity:
We know that acceleration can also be expressed in terms of velocity and distance:
a=vdvdx
Substitute a=12√x:
12√x=vdvdx
6. Separate Variables:
Rearranging gives:
vdv=12√xdx
7. Integrate Both Sides:
Integrate the left side with respect to v and the right side with respect to x:
∫vdv=∫12√xdx
This results in:
v22=12⋅23x3/2+C
Simplifying gives:
v22=8x3/2+C
8. Determine the Constant of Integration C:
Since the particle starts from rest when x=0 (initial velocity v=0):
0=8⋅03/2+C⟹C=0
Thus, we have:
v22=8x3/2
9. Solve for Velocity v:
Multiply both sides by 2:
v2=16x3/2
Taking the square root gives:
v=4x3/2
10. Substitute x=16:
Now substitute x=16 to find v:
v=4⋅(16)3/2
Calculate (16)3/2=(42)3/2=43=64:
v=4⋅64=256 m/s
Final Answer:
The velocity of the particle at the instant when its acceleration is 48 m/s² is:
32 m/s
We are given the acceleration as:
a=12√x
We need to find the distance x when the acceleration a is 48 m/s². Set the equation equal to 48:
12√x=48
Divide both sides by 12:
√x=4812=4
x=42=16 m
We know that acceleration can also be expressed in terms of velocity and distance:
a=vdvdx
Substitute a=12√x:
12√x=vdvdx
Rearranging gives:
vdv=12√xdx
Integrate the left side with respect to v and the right side with respect to x:
∫vdv=∫12√xdx
This results in:
v22=12⋅23x3/2+C
Simplifying gives:
v22=8x3/2+C
Since the particle starts from rest when x=0 (initial velocity v=0):
0=8⋅03/2+C⟹C=0
Thus, we have:
v22=8x3/2
Multiply both sides by 2:
v2=16x3/2
Taking the square root gives:
v=4x3/2
Now substitute x=16 to find v:
v=4⋅(16)3/2
Calculate (16)3/2=(42)3/2=43=64:
v=4⋅64=256 m/s
The velocity of the particle at the instant when its acceleration is 48 m/s² is:
32 m/s
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE MAIN (archive)
19 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 1
75 Videos
- JEE MAIN REVISON TEST-23BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)
1 Video
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
Similar Questions
A particle starts from rest, moving in a straight line with a time varying acceleration (inm/s2):a=30−152√t, where time is in seconds . The displacement of the particle in 4 seconds is .
View SolutionA particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
View Solution
Knowledge Check
A particle starts from point A moves along a straight line path with an acceleration given by a = p - qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
ApqBp√qCqpD√qp
A particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q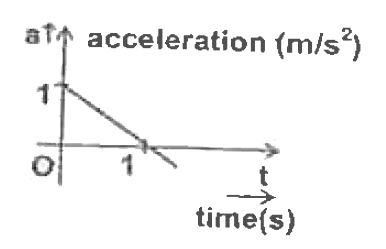
View SolutionStarting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
View SolutionA particle moving along a straight line with a constant acceleration of −4m/s2 passes through a point A on the line with a velocity of +8m/s at some moment. Find the distance travelled by the particle in 5 seconds after that moment.
View SolutionA particle moving along a straight line with a constant acceleration of −4m/s2 passes through a point A on the line with a velocity of +8m/s at some moment. Find the distance travelled by the particle in 5 seconds after that moment.
View SolutionA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View Solution

