A particle thrown up vertically from the ground at reaches its highest point at t=t0 =The displacement of the particle between t=7t08andt=t0 is S. Then u2Sg=
The correct Answer is:A, B
To solve the problem step by step, we will analyze the motion of a particle thrown vertically upward and derive the required expression.
1. Understanding the Motion:
- A particle is thrown vertically upward with an initial velocity u.
- It reaches its highest point at time t=t0, where the final velocity v=0.
2. Finding the Time to Reach Maximum Height:
- At the highest point, the velocity is zero. Using the equation of motion:
v=u−gt
Setting v=0 at t=t0:
0=u−gt0⟹t0=ug
3. Displacement Between Specific Times:
- We need to find the displacement S between t=7t08 and t=t0.
- The displacement can be calculated using the formula:
S=hmax−h
- Here, hmax is the maximum height reached, and h is the height at t=7t08.
4. Calculating Maximum Height hmax:
- Using the equation:
hmax=u22g
5. Finding Height at t=7t08:
- Substitute t=7t08 into the displacement formula:
h=ut−12gt2
- Substitute t0=ug:
h=u(7u8g)−12g(7u8g)2
- Simplifying:
h=7u28g−12g⋅49u264g2
h=7u28g−49u2128g
- Finding a common denominator:
h=112u2128g−49u2128g=63u2128g
6. Calculating Displacement S:
- Now substitute hmax and h into the displacement formula:
S=hmax−h=u22g−63u2128g
- Finding a common denominator:
S=64u2128g−63u2128g=u2128g
7. Finding the Required Ratio:
- We need to find u2Sg:
u2Sg=u2(u2128g)g=u2⋅128gu2g=128
Final Answer:
u2Sg=128
- A particle is thrown vertically upward with an initial velocity u.
- It reaches its highest point at time t=t0, where the final velocity v=0.
- At the highest point, the velocity is zero. Using the equation of motion:
v=u−gt
Setting v=0 at t=t0:
0=u−gt0⟹t0=ug
- We need to find the displacement S between t=7t08 and t=t0.
- The displacement can be calculated using the formula:
S=hmax−h
- Here, hmax is the maximum height reached, and h is the height at t=7t08.
- Using the equation:
hmax=u22g
- Substitute t=7t08 into the displacement formula:
h=ut−12gt2
- Substitute t0=ug:
h=u(7u8g)−12g(7u8g)2
- Simplifying:
h=7u28g−12g⋅49u264g2
h=7u28g−49u2128g
- Finding a common denominator:
h=112u2128g−49u2128g=63u2128g
- Now substitute hmax and h into the displacement formula:
S=hmax−h=u22g−63u2128g
- Finding a common denominator:
S=64u2128g−63u2128g=u2128g
- We need to find u2Sg:
u2Sg=u2(u2128g)g=u2⋅128gu2g=128
u2Sg=128
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE MAIN (archive)
19 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 1
75 Videos
- JEE MAIN REVISON TEST-23BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)
1 Video
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
Similar Questions
Knowledge Check
A particle is projected vertically upwards and it reaches the maximum height H in time T seconds. The height of the particle at any time t will be-
Ag(t−T)2BH−12g(t−T)2C12g(t−T)2DH−g(t−T)2
If the displacement of a particle varies with time as x=5t2+7t.
Then find its velocity.
View SolutionLet A, B and C be points in a vertical line at height h, 4h5andh5 and from the ground. A particle released from rest from the point A reaches the ground in time T. The time taken by the particle to go from B to C is TBC . Then T(TBC)2=
View SolutionA particle is projected vertically from the ground takes time t1=1s upto point A, t2=3s from point A to B, and time t3=4s from point B to highest point. Find the height of the middle point of A and B from the ground.
View SolutionA particle moves on x-axis as per equation x=(t3−9t2+15+2)m. Distance travelled by the particle between t=0 and t=5s is
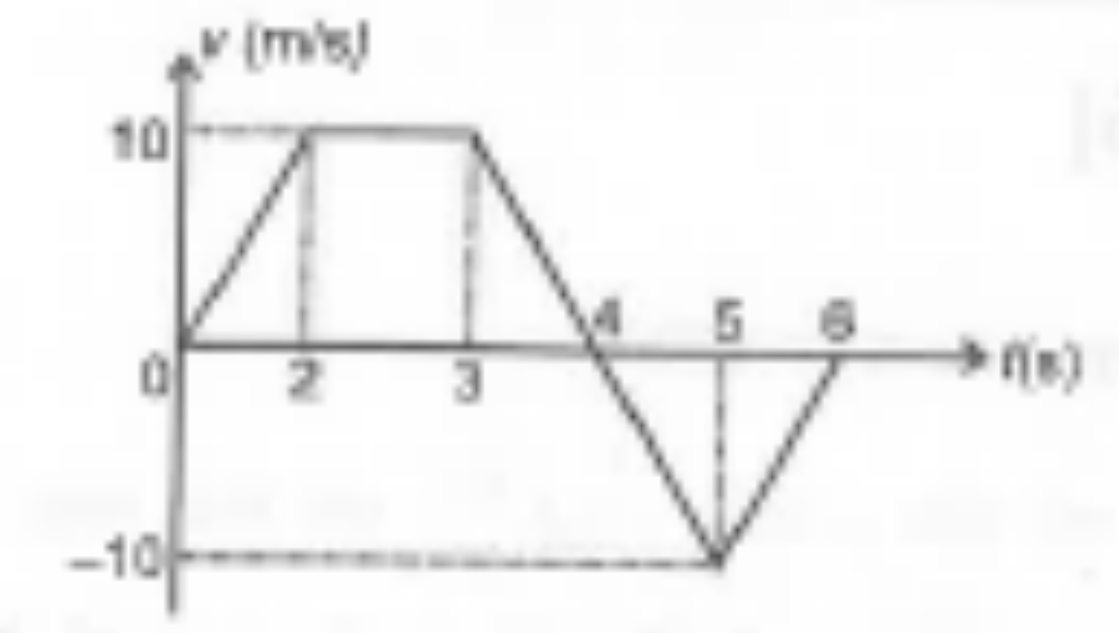
View SolutionThe velocity (v)-time (t) graph of a partide moving along a straight line is as shown in the figure. The displacement of the particle from t = 0 to t = 4 is
View Solutionx−t graph of a particle in SHM is
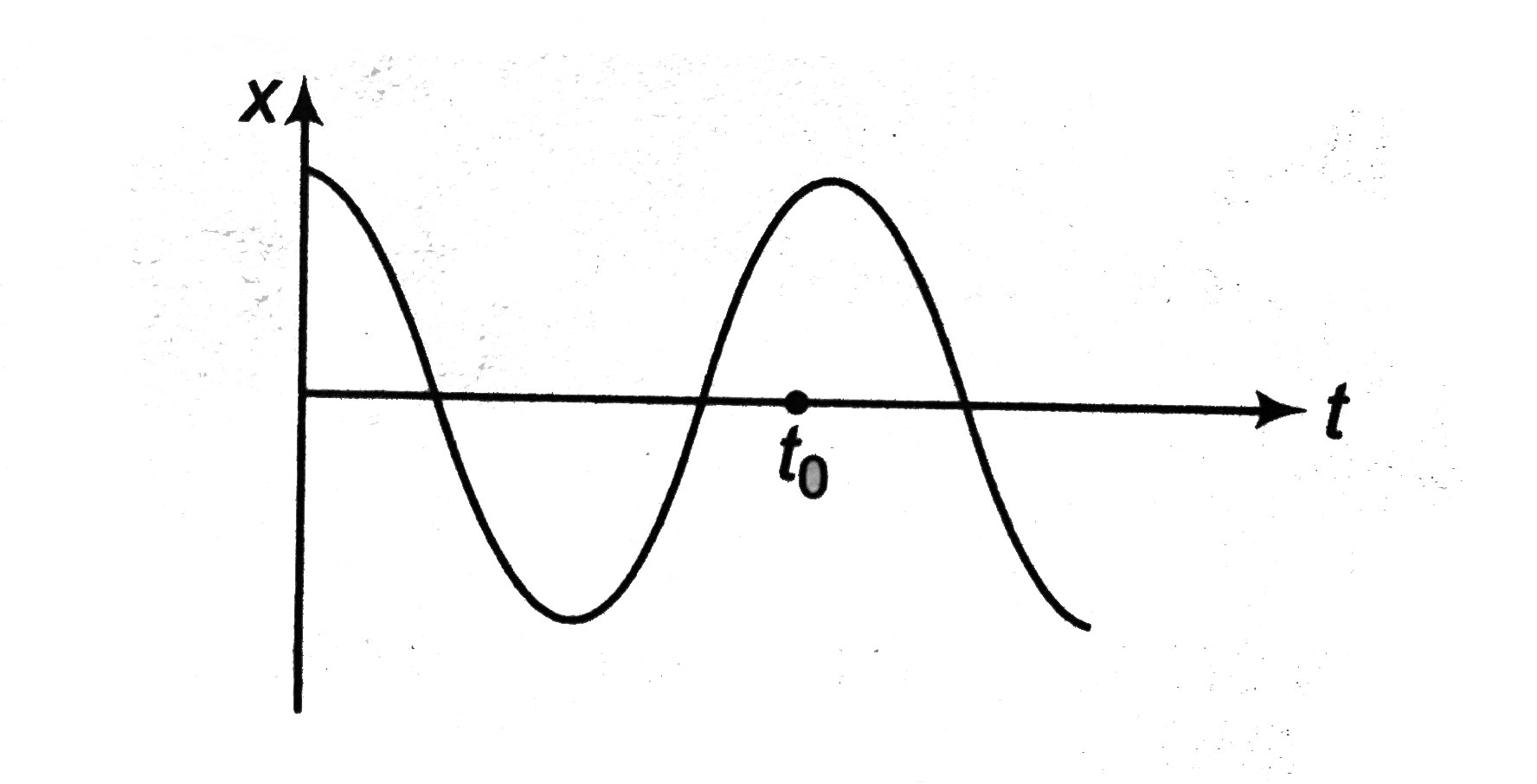
At time t=t0, what are the signs of v and a of the particle?
View SolutionA particle is moving with a velocity of v=(3+6t+9t2)ms. Find out
(a) the acceleration of the particle at t=3s.
(b) the displacement of the particle in the interval t=5s to t=8s.
View Solution

