Velocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
To solve the problem of finding the displacement of a particle whose velocity varies with time as v=4t between t=2 seconds and t=4 seconds, we can follow these steps:
Step 1: Understand the relationship between velocity and displacement
The velocity of a particle is defined as the rate of change of displacement with respect to time. Mathematically, this can be expressed as:
v=dsdt
where s is the displacement.
Step 2: Set up the equation for displacement
Given that the velocity v is 4t, we can write:
dsdt=4t
Step 3: Integrate to find displacement
To find the displacement s, we need to integrate the velocity function with respect to time. We can rearrange the equation and integrate:
ds=4tdt
Integrating both sides from t=2 to t=4:
∫ss0ds=∫424tdt
Step 4: Calculate the integral
The left side becomes:
s−s0
For the right side, we calculate the integral:
∫4tdt=4⋅t22=2t2
Now we evaluate this from t=2 to t=4:
2t2∣∣∣42=2(42)−2(22)=2(16)−2(4)=32−8=24
Step 5: Conclusion
Thus, the displacement s from t=2 seconds to t=4 seconds is:
s=24 meters
Final Answer
The displacement of the particle between t=2 seconds and t=4 seconds is 24 meters.
---
The velocity of a particle is defined as the rate of change of displacement with respect to time. Mathematically, this can be expressed as:
v=dsdt
where s is the displacement.
Given that the velocity v is 4t, we can write:
dsdt=4t
To find the displacement s, we need to integrate the velocity function with respect to time. We can rearrange the equation and integrate:
ds=4tdt
Integrating both sides from t=2 to t=4:
∫ss0ds=∫424tdt
The left side becomes:
s−s0
For the right side, we calculate the integral:
∫4tdt=4⋅t22=2t2
Now we evaluate this from t=2 to t=4:
2t2∣∣∣42=2(42)−2(22)=2(16)−2(4)=32−8=24
Thus, the displacement s from t=2 seconds to t=4 seconds is:
s=24 meters
The displacement of the particle between t=2 seconds and t=4 seconds is 24 meters.
Topper's Solved these Questions
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:EXERCISE-1
Explore 99 Videos
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:EXERCISE-2
Explore 170 Videos
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:Integer Type Question
Explore 3 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
Similar Questions
If the displacement of a particle varies with time as √x=t+3
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View SolutionThe position x of a particle varies with time t as x=at2−bt3.The acceleration of the particle will be zero at time t equal to
View SolutionVelocity of a particle at any time t is v=(2ˆi+2tˆj)m/s. Find acceleration and displacement of particle at t=1s. Can we apply v=u+at or not?
View Solutionthe angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
View SolutionThe position x of a particle varies with time t as x=at2−bt3. The acceleration at time t of the particle will be equal to zero, where (t) is equal to .
View SolutionThe position x of a particle varies with time t as x=at2−bt3. The acceleration at time t of the particle will be equal to zero, where (t) is equal to .
View SolutionFigure given here shows the variation of velocity of a particle with time.
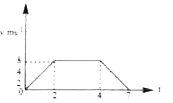
Find the following:
(i) Displacement during the time intervals.
(a) 0 to 2 sec., (b) 2 to 4 sec. and (c) 4 to 7 sec
(ii) Accelerations at
(a)t = 1 sec, (b) t = 3 sec. and (c)t = 6 sec.
(iii) Average acceleration
(a) between t = 0 to t = 4 sec.
(b) between t = 0 to t = 7 sec.
(iv) Average velocity during the motion.
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionIf the displacement of a particle varies with time as x=5t2+7t.
Then find its velocity.
View Solution

