Acceleration of a particle is increasing linearly with time. Its acceleration is 10 m/s2att=0and20m/s2att=5s.Also, its speed is 5m/s at t =0 and its positions is x= -100m at t =0 .Find at time t its acceleration ,velocity and positions.
a=mt+c
At t= 0 , a = 10 " "rArr 10 = c <br>Att=5,a=20 ⇒ 20=5m+C⇒ 20=5m+10 ⇒m=2 ∴a=2t+10
dvdt=2t+10⇒∫v5dv=∫t0(2t+10)dt ⇒ v−5=t2+10t ⇒ v=t2+10t+5
dxdt=t2+10t+5 ⇒ ∫x−100dx=∫t0(t2+10t+5)dt ⇒
x+100=t33+5t2+5t⇒x=t33+5t2+5t−100
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 1
75 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 2
65 Videos
- JEE MAIN REVISON TEST-23BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)
1 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
Similar Questions
The distance s of a particle in time t is given by s=t3−6t2−4t−8. Its acceleration vanishes at t=
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
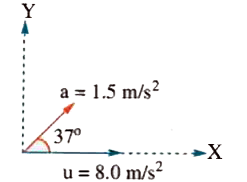
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionVelocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View SolutionAcceleration of a particle is given by
a=1/V
Where V is the velocity . Find
(i) Velocity of particle at time t, given that v = 10 m/s at t = 0.
(ii) Velocity of particle when its position is x, given that speed is 3 m/s at x = 0.
View SolutionA particle is moving with uniform acceleration. Its position (x) is given in terms of time (t in s ) as x=(5t2+4t+8), then
Its initial velocity is 8m/s
Its velocity at time t=3s is 36m/s
Its acceleration is 5m/s2
Its position at t=2 s is 36 m
View SolutionAcceleration of a particle is given by
a=3t2+2t+1
Where t is time . Find
(i) its velocity at time t assuming velocity to be 10 m/s at t = 0.
(ii) its position at time t assuming that the particle is at origin at t = 0.
(iii) What is the average speed of the particle in the duration t = 0 to t = 1s?
(iv) What is the average acceleration of the particle in the duration t = 0 to t = 1s?
View SolutionAcceleration of a particle in x-y plane varies with time as a=(2tˆi+3t2ˆj)m/s2 At time t=0, velocity of particle is 2m/s along positive x direction and particle starts from origin. Find velocity and coordinates of particle at t=1s.
View SolutionA particle moving with uniform acceleration passes the point x=2m with velocity 20m/s at the instant t=0. Some time later it is observed at the point x=32m moving with velocity 10m/s.
(a) What is its acceleration?
(b) Find its position nd velocity at the instant t=8s.
(c) What is the distance traveled during the interval t=0 to 8s?
View SolutionThe acceleration time graph of a particle is shown in the Fig. 2 (CF). 11. At time t=0s velocity of the particle is 8ms−1. Its velocity t=10s is.
 .
.
View Solution
