There is an infinite line of uniform linear density of charge . A particle of charge and mass 'm' is projected with initial velocity at an angle with the line of charge at a distance 'a' from it. The speed of the particle is found to be minimum when its distance from the line of charge is . Find the value of . Neglect gravity

The correct Answer is:1
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 106 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
Similar Questions
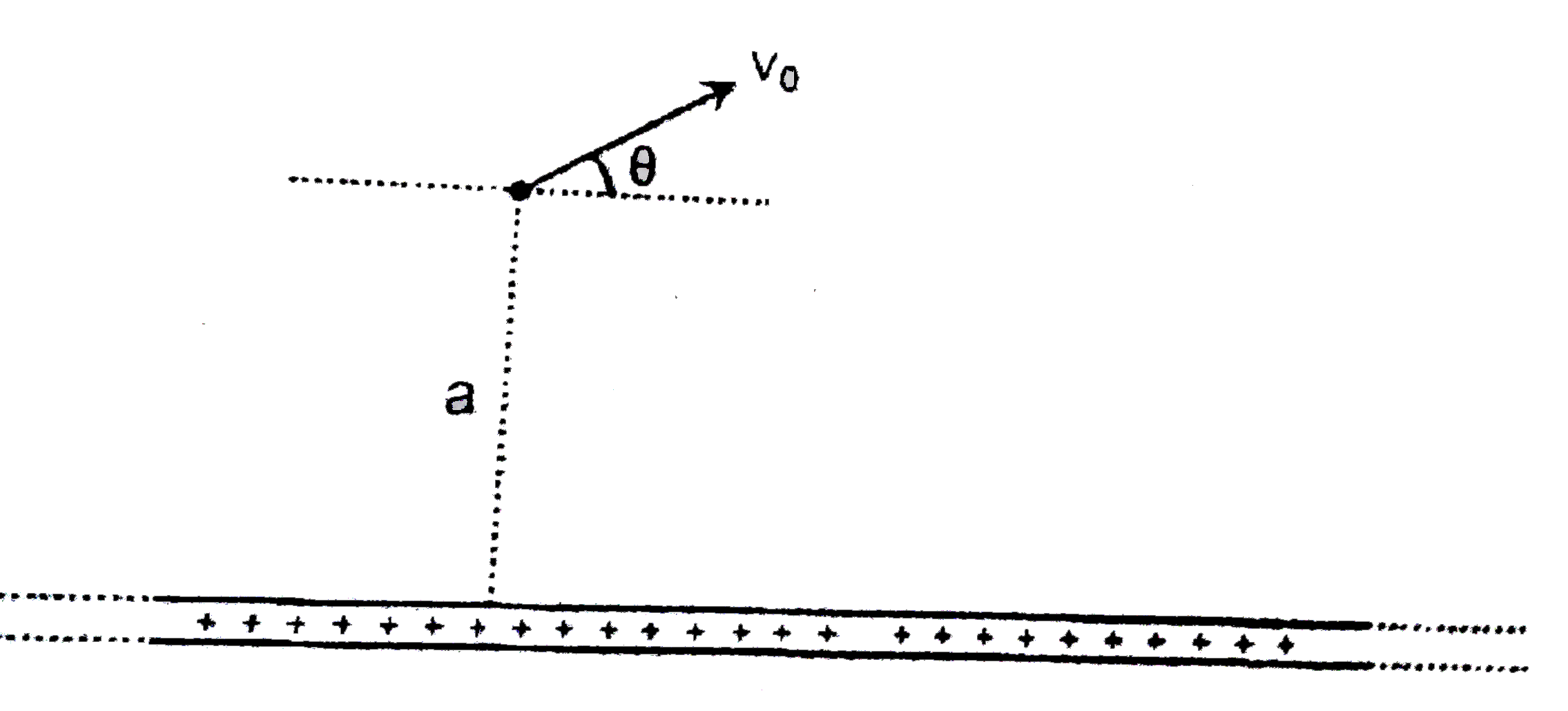
There is an infinite line of uniform linear density of charge +λ. A particle of charge −q & mass m is projected with initial velocity v0 at an angle θ with the line of charge from a distance a from it. The point charge moves in plane containing line charge and point of projection The speed of the particle of found to be minimum when it's distance from the line of charge is ae(nπmε20/qλ). The value of n is (ingnore gravity)
View SolutionA particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.

View SolutionTwo infinite long wires, each carrying current I, are lying along x- and y-axis, respectively. A charged particle, having a charge q and mass m, is projected with a velocity u along the straight line OP. The path of the particle is (neglect gravity)

View SolutionA particle of charge q and mass m is moving with a velocity −vˆi(v≠0) towards a large screen placed in the Y-Z plane at a distance d. If there is a magnetic field →B=B0ˆk , the minimum value of v for which the particle will not hit the screen is :
View SolutionA particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionIn the figure shown there is a large sheet of charge of uniform surface charge density'σ'.A charge particle of charge '−q' and mass 'm' is projected from a point A on the sheet with a speed 'u' with the angle of projection such that it lands at maximum distance from A on the sheet. Neglecting gravity, find the time flight

View SolutionA particle of charge q and mass m is projected from the origin with velocity v=v0ˆi in a non uniformj magnetic fiedl B=−B0xˆk. Here v0 and B0 are positive constants of proper dimensions. Find the maximum positive x coordinate of the particle during its motion.
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionA positive charge is released from rest at a distance r0 from a positive line charge with uniform density . The speed (v) of the point charge , as a function of instantaneous distance r from line charge, is proportional to:
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View Solution

