A particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
To solve the problem, we will use the principle of conservation of energy. The total mechanical energy (kinetic energy + potential energy) of the system remains constant if only conservative forces are acting.
1. Identify the Given Values:
- Mass of the particle, m=100g=0.1kg
- Charge of the particle, q1=2μC=2×10−6C
- Fixed charge, q2=5μC=5×10−6C
- Initial distance from the fixed charge, ri=50cm=0.5m
- Final distance from the fixed charge, rf=3m
2. Calculate Initial Potential Energy (U_i):
The potential energy between two point charges is given by the formula:
U=kq1q2r
where k=9×109N m2/C2.
For initial potential energy:
Ui=kq1q2ri=9×109(2×10−6)(5×10−6)0.5
Ui=9×10910×10−120.5=9×109×20×10−12=180×10−3J=0.18J
3. Calculate Final Potential Energy (U_f):
For final potential energy:
Uf=kq1q2rf=9×109(2×10−6)(5×10−6)3
Uf=9×10910×10−123=9×109×10×10−123=30×10−3J=0.03J
4. Apply Conservation of Energy:
The change in potential energy equals the change in kinetic energy:
Kf−Ki=Ui−Uf
Since the particle starts from rest, Ki=0:
Kf=Ui−Uf=0.18J−0.03J=0.15J
5. Relate Kinetic Energy to Speed:
The kinetic energy is given by:
K=12mv2
Setting this equal to Kf:
0.15=12(0.1)v2
0.15=0.05v2
v2=0.150.05=3
v=√3m/s≈1.732m/s
Final Answer:
The speed of the particle when its distance from the fixed charge becomes 3 m is approximately √3m/s.
- Mass of the particle, m=100g=0.1kg
- Charge of the particle, q1=2μC=2×10−6C
- Fixed charge, q2=5μC=5×10−6C
- Initial distance from the fixed charge, ri=50cm=0.5m
- Final distance from the fixed charge, rf=3m
The potential energy between two point charges is given by the formula:
U=kq1q2r
where k=9×109N m2/C2.
Ui=kq1q2ri=9×109(2×10−6)(5×10−6)0.5
Ui=9×10910×10−120.5=9×109×20×10−12=180×10−3J=0.18J
For final potential energy:
Uf=kq1q2rf=9×109(2×10−6)(5×10−6)3
Uf=9×10910×10−123=9×109×10×10−123=30×10−3J=0.03J
The change in potential energy equals the change in kinetic energy:
Kf−Ki=Ui−Uf
Since the particle starts from rest, Ki=0:
Kf=Ui−Uf=0.18J−0.03J=0.15J
The kinetic energy is given by:
K=12mv2
Setting this equal to Kf:
0.15=12(0.1)v2
0.15=0.05v2
v2=0.150.05=3
v=√3m/s≈1.732m/s
The speed of the particle when its distance from the fixed charge becomes 3 m is approximately √3m/s.
Similar Questions
Two identical charges, 5μC each are fixed at a distance 8 cm and a charged particle of mass 9×10−6kg and charge −10μC is placed at a distance 5 cm from each of them and is released. Find the speed of the particle when it is nearest to the two charges.
View SolutionA particle of mass 2 g and charge 1μC is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.

View SolutionTwo point charges, each of mass m and charge q are released when they are at a distance d from each other. What is the speed of each charged particle when they are at a distance 2r ?
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionTwo circular rings A and B each of radius a = 30 cm are placed coaxially with their axis horizontal in a uniform electric field E=105NC−1 directed vertically upward as shown in figure. Distance between centers of the rings A and B (CAandCB)is40cm. Ring A has positive charge qA=10μC and B has a negative charge qB=−20μC. A particle of mass m and charge q=10μC is released from rest at the center of ring A. If particle moves along CACB, then
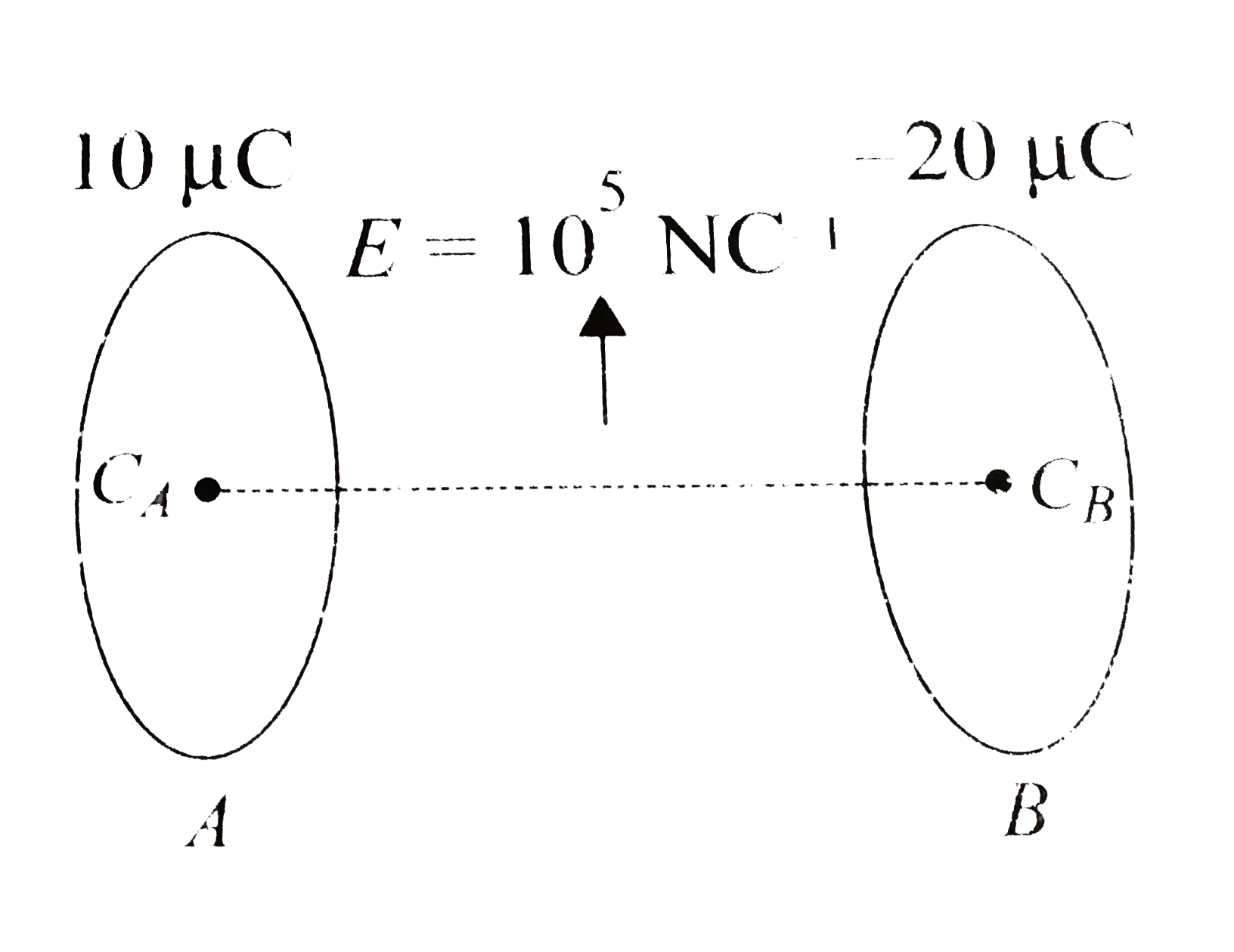
Speed of particle when it reaches at center of B is
View SolutionA charged particle of charge 'Q' is held fixed and another charged particle of mass 'm' and charge 'q' (of the same sign) is released from a distance 'r'. The impulse of the force exerted by the external agent on the fixed charge by the time distance between 'Q' and 'q' becomes 2r is
View SolutionTwo point charges q1=q2=2μC are fixed at x1=+3m and x2=−3m as shown in figure. A third particle of mass 1 g and charge q3=−4μC are released from rest at y=4.0m.Find the speed of the particle as it reaches the origin.
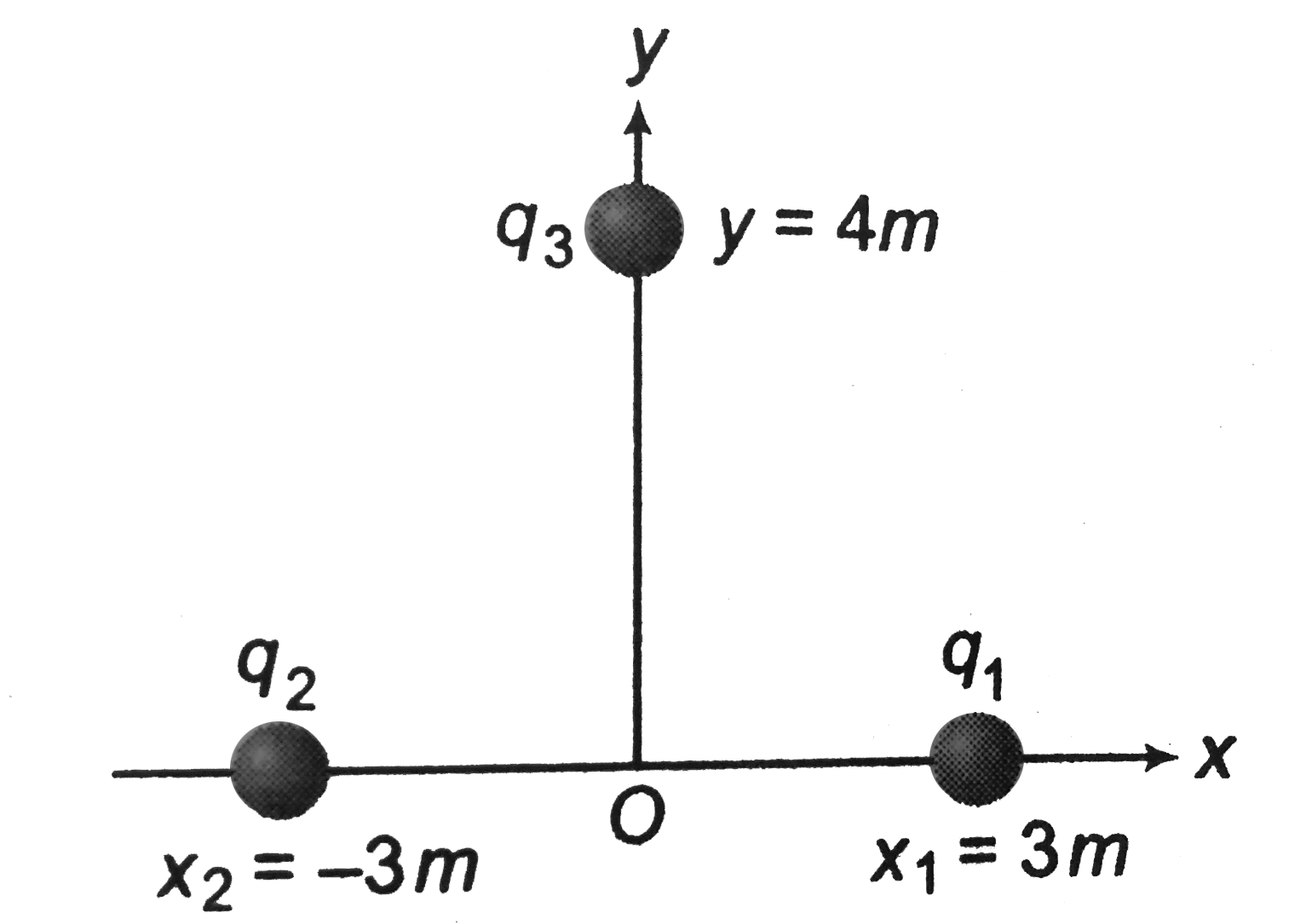
View SolutionTwo point charges q1=q2=2μC are fixed at x1=+3m and x2=−3m as shown in figure. A third particle of mass 1 g and charge q3=−4μC are released from rest at y=4.0m.Find the speed of the particle as it reaches the origin.

View Solution
