A long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
√qλlnrπm∈0
√qλln2πm∈0
√qλln22πm∈0
√qλln2πm∈0
The correct Answer is:B
To solve the problem, we need to determine the speed of a charged particle as it moves from a distance r to a distance 2r from a long straight wire that has a linear charge density λ. We will use the concepts of electric field, work done, and the work-energy theorem.
1. Electric Field due to the Wire:
The electric field E at a distance x from a long straight wire with linear charge density λ is given by:
E=λ2πϵ0x
where ϵ0 is the permittivity of free space.
2. Force on the Particle:
The force F acting on the particle of charge q in the electric field is:
F=qE=q⋅λ2πϵ0x
3. Work Done by the Electric Force:
The work done W by the electric force when the particle moves from distance r to 2r can be calculated by integrating the force over the distance:
W=∫2rrFdx=∫2rrq⋅λ2πϵ0xdx
This simplifies to:
W=qλ2πϵ0∫2rr1xdx
The integral of 1x is lnx, so:
W=qλ2πϵ0(ln(2r)−ln(r))=qλ2πϵ0ln(2rr)=qλ2πϵ0ln(2)
4. Using the Work-Energy Theorem:
According to the work-energy theorem, the work done on the particle is equal to the change in kinetic energy. Since the particle starts from rest, the initial kinetic energy is zero:
W=ΔKE=KEf−KEi=12mv2−0
Therefore:
qλ2πϵ0ln(2)=12mv2
5. Solving for the Speed v:
Rearranging the equation to solve for v:
mv2=2qλ2πϵ0ln(2)
v2=qλln(2)mπϵ0
v=√qλln(2)mπϵ0
Final Answer:
The speed of the particle as it crosses the point at a distance 2r from the wire is:
v=√qλln(2)mπϵ0
The electric field E at a distance x from a long straight wire with linear charge density λ is given by:
E=λ2πϵ0x
where ϵ0 is the permittivity of free space.
The force F acting on the particle of charge q in the electric field is:
F=qE=q⋅λ2πϵ0x
The work done W by the electric force when the particle moves from distance r to 2r can be calculated by integrating the force over the distance:
W=∫2rrFdx=∫2rrq⋅λ2πϵ0xdx
This simplifies to:
W=qλ2πϵ0∫2rr1xdx
The integral of 1x is lnx, so:
W=qλ2πϵ0(ln(2r)−ln(r))=qλ2πϵ0ln(2rr)=qλ2πϵ0ln(2)
According to the work-energy theorem, the work done on the particle is equal to the change in kinetic energy. Since the particle starts from rest, the initial kinetic energy is zero:
W=ΔKE=KEf−KEi=12mv2−0
Therefore:
qλ2πϵ0ln(2)=12mv2
Rearranging the equation to solve for v:
mv2=2qλ2πϵ0ln(2)
v2=qλln(2)mπϵ0
v=√qλln(2)mπϵ0
The speed of the particle as it crosses the point at a distance 2r from the wire is:
v=√qλln(2)mπϵ0
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.57
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.58
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.55
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Two point charges, each of mass m and charge q are released when they are at a distance d from each other. What is the speed of each charged particle when they are at a distance 2r ?
View SolutionA particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is
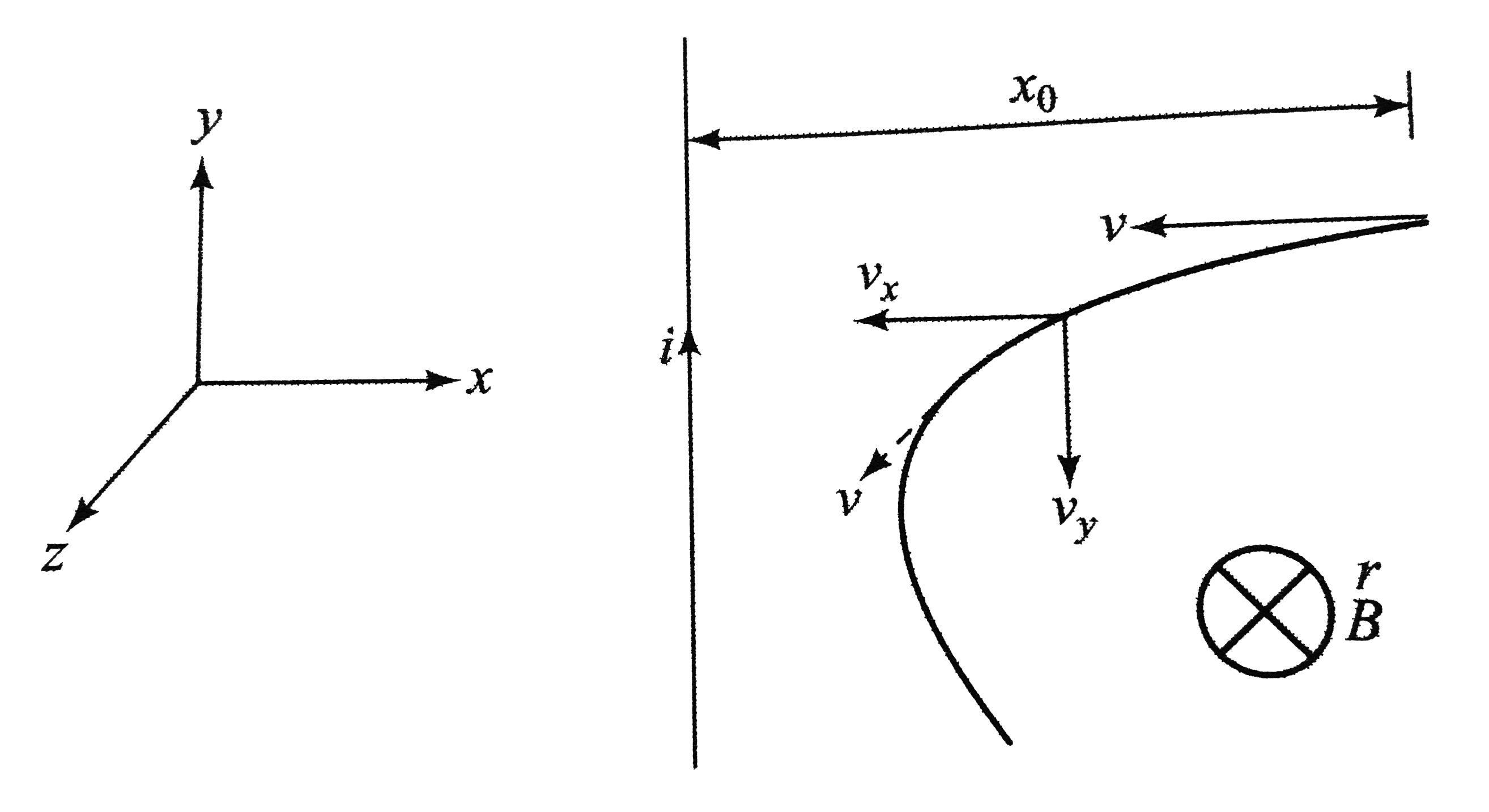
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.

View Solution_S01_013_Q01.png)
A very small groove is made in the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle for that place.
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionTwo identical charges, 5μC each are fixed at a distance 8 cm and a charged particle of mass 9×10−6kg and charge −10μC is placed at a distance 5 cm from each of them and is released. Find the speed of the particle when it is nearest to the two charges.
View SolutionA long , straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance x_0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.
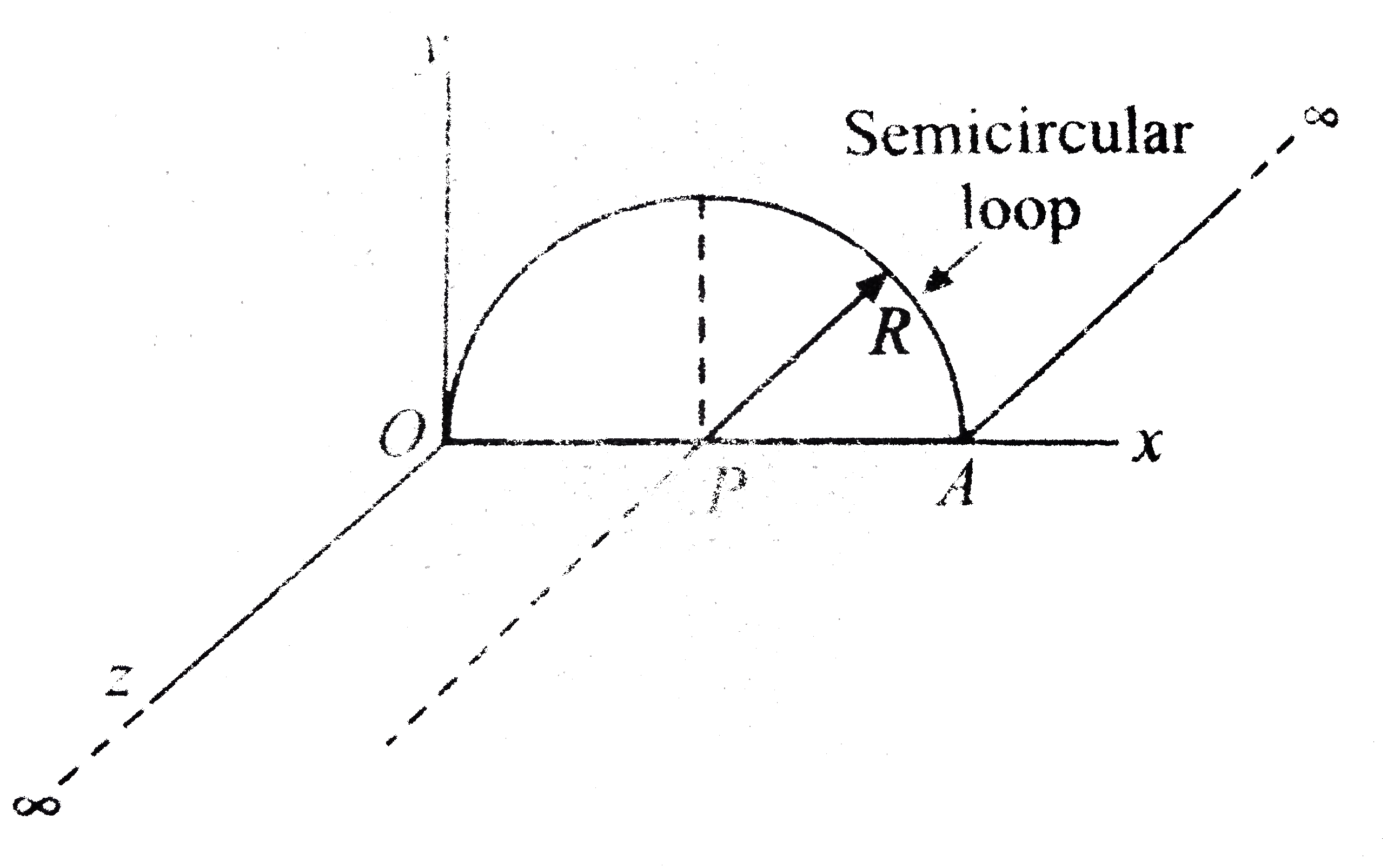
View SolutionAn infinte wire having linear charge density λ is arranged as shown in fig. A charge particle of mass m and charge q is released charged q is released from point P. Find the initial acceleration of the particle just after the particle is released.
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x is very less than R, find the time period of oscillation of the particle if it is released from there.
View Solution
