The time periods - hence the frequencies (f) and the amplitudes (A) of the driven pendulums in steady state are measured. The variation of A with f is correctly shown by the graph.
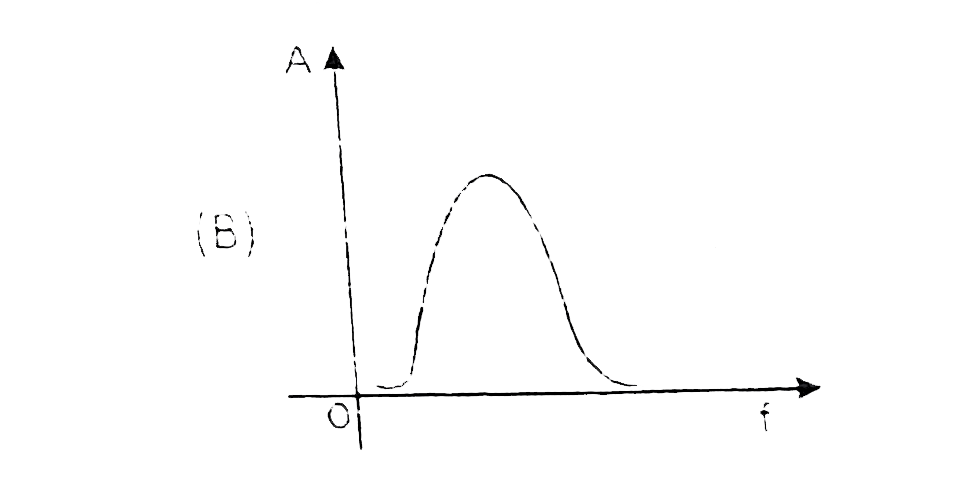

The correct Answer is:B
To solve the problem regarding the variation of amplitude (A) with frequency (f) for driven pendulums in steady state, we need to analyze the behavior of the system as frequency changes. Here’s a step-by-step breakdown of the solution:
Step 1: Understanding the System
In a driven pendulum, the amplitude of oscillation depends on the frequency of the driving force. As the frequency approaches the natural frequency of the pendulum, resonance occurs, leading to a significant increase in amplitude.
Hint: Consider how resonance affects the amplitude of oscillation in a driven system.
Step 2: Analyzing the Options
We have four options that describe the relationship between amplitude and frequency. We need to evaluate each option based on the expected behavior of a driven pendulum.
Hint: Look for patterns in the graphs that indicate how amplitude changes as frequency is varied.
Step 3: Evaluating Option 1
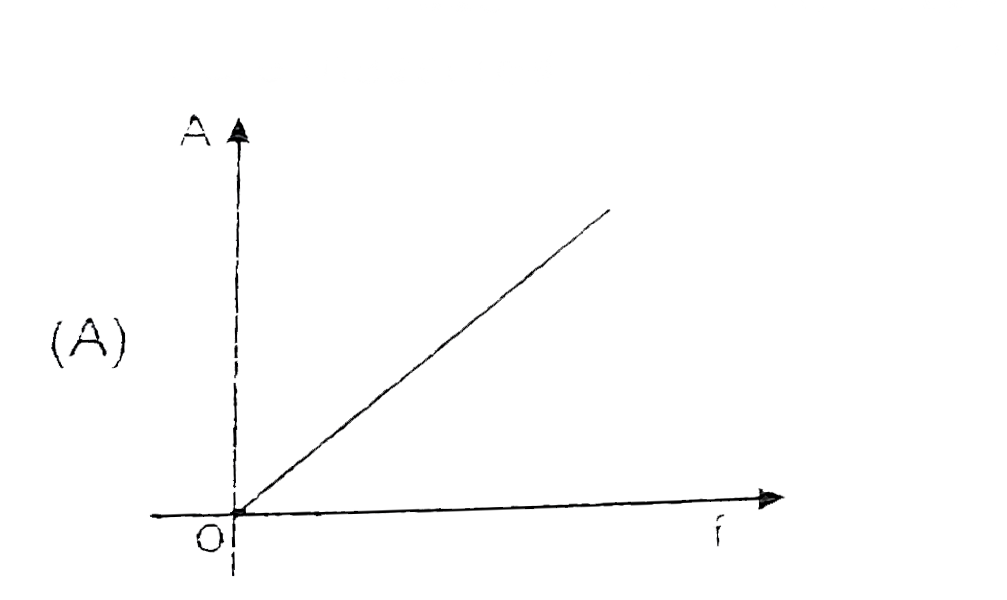
Option 1 suggests a linear increase in amplitude with frequency. This implies that as frequency increases, amplitude continuously increases without any limit.
Hint: Think about whether amplitude can increase indefinitely with frequency in a real system.
Step 4: Evaluating Option 2
Option 2 shows a curve that increases with frequency until it reaches a maximum (resonance) and then decreases. This is characteristic of a driven oscillator where amplitude peaks at resonance.
Hint: Recall the concept of resonance and how it affects amplitude in oscillatory systems.
Step 5: Evaluating Option 3
Option 3 indicates that amplitude remains constant regardless of frequency. This scenario does not reflect the behavior of a driven pendulum, especially near resonance.
Hint: Consider if it's physically plausible for amplitude to remain unchanged with varying frequency.
Step 6: Evaluating Option 4
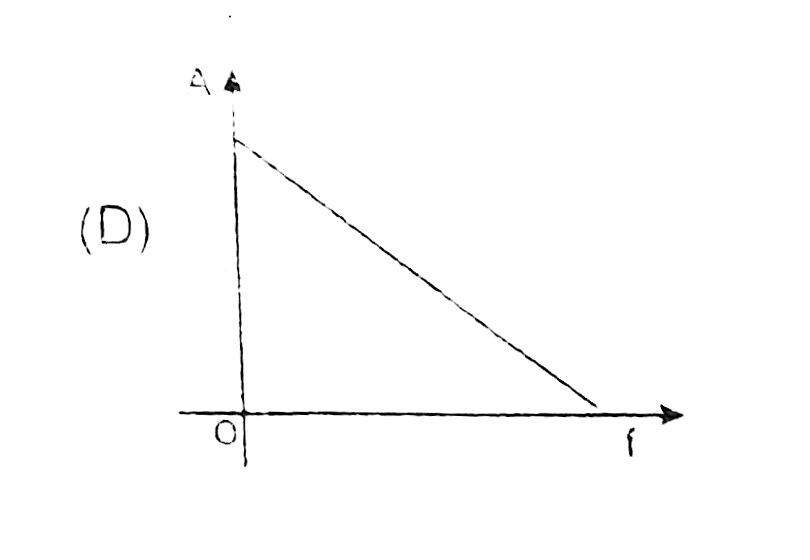
Option 4 suggests that amplitude decreases linearly as frequency increases. This is contrary to the expected behavior of a driven pendulum.
Hint: Think about the relationship between frequency and amplitude in the context of resonance.
Step 7: Conclusion
After evaluating all options, Option 2 is the correct representation of the relationship between amplitude and frequency for a driven pendulum in steady state. The graph shows that amplitude increases with frequency until it reaches a maximum at the resonant frequency, after which it decreases.
Final Answer: The correct option is Option 2.
In a driven pendulum, the amplitude of oscillation depends on the frequency of the driving force. As the frequency approaches the natural frequency of the pendulum, resonance occurs, leading to a significant increase in amplitude.
We have four options that describe the relationship between amplitude and frequency. We need to evaluate each option based on the expected behavior of a driven pendulum.
Option 1 suggests a linear increase in amplitude with frequency. This implies that as frequency increases, amplitude continuously increases without any limit.
Option 2 shows a curve that increases with frequency until it reaches a maximum (resonance) and then decreases. This is characteristic of a driven oscillator where amplitude peaks at resonance.
Option 3 indicates that amplitude remains constant regardless of frequency. This scenario does not reflect the behavior of a driven pendulum, especially near resonance.
Option 4 suggests that amplitude decreases linearly as frequency increases. This is contrary to the expected behavior of a driven pendulum.
After evaluating all options, Option 2 is the correct representation of the relationship between amplitude and frequency for a driven pendulum in steady state. The graph shows that amplitude increases with frequency until it reaches a maximum at the resonant frequency, after which it decreases.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.579videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.5820videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.559videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
The period of the function f(x)=kcoskx is π2. The amplitude of f is
A14B12C1D4
The correct variation of resistance R with frequency f is given by
View SolutionThe graph between time period (T) and length (l) of a simple pendulum is
View SolutionA large number of pendulums with identical bobs (mass m) but varying lengths are suspended from a thick thread. Another pendulum of a heavier bob (mass M) is also suspended from the same thred as shown.

This pendulum with the heavier bob is used as a 'driver' to drive the other pendulums called as 'driven' pendulums. Assume that the amplitude of the driver is maintained constant (by some suitable mechanism). Let the frequency of the driver be f0
The variation of amplitude A with respect to time t is shown asView SolutionA large number of pendulums with identical bobs (mass m) but varying lengths are suspended from a thick thread. Another pendulum of a heavier bob (mass M) is also suspended from the same thred as shown.

This pendulum with the heavier bob is used as a 'driver' to drive the other pendulums called as 'driven' pendulums. Assume that the amplitude of the driver is maintained constant (by some suitable mechanism). Let the frequency of the driver be f0
Which of the following will give a straight line graph ?View SolutionA large number of pendulums with identical bobs (mass m) but varying lengths are suspended from a thick thread. Another pendulum of a heavier bob (mass M) is also suspended from the same thred as shown.

This pendulum with the heavier bob is used as a 'driver' to drive the other pendulums called as 'driven' pendulums. Assume that the amplitude of the driver is maintained constant (by some suitable mechanism). Let the frequency of the driver be f0
The above pendulum is set into oscillation with an initial amplitude of 10.0 cm. Soon this pendulum comes to rest momentarily and the driver is seen to oscillate with an amplitude of 8.16 cm. Then mass M equalsView SolutionThe time period of a simple pendulum is 2 s. Find its frequency .
View SolutionA large number of pendulums with identical bobs (mass m) but varying lengths are suspended from a thick thread. Another pendulum of a heavier bob (mass M) is also suspended from the same thred as shown.

This pendulum with the heavier bob is used as a 'driver' to drive the other pendulums called as 'driven' pendulums. Assume that the amplitude of the driver is maintained constant (by some suitable mechanism). Let the frequency of the driver be f0
It is observed thatView Solution
