On face of a glass (μ=1.50) lens is coated with a thin film of magnesium fluoride MgF2(μ=1.38) to reduce reflection from the lens surface. Assuming the incident light to be perpendicular to the lens surface. The least coating thickness that eliminates the reflection at the centre of the visible spectrum (λ=550nm) is about
0.05μm
0.10μm
1.38μm
2.80μm
The correct Answer is:B
To solve the problem, we need to find the least thickness of the magnesium fluoride (MgF₂) coating that will eliminate reflection from the surface of the glass lens. This occurs due to destructive interference of light waves reflected from the air-film interface and the film-glass interface.
1. Understanding Destructive Interference:
For destructive interference to occur, the path difference between the two reflected rays must be an odd multiple of half wavelengths. The condition for destructive interference is given by:
Δx=(2n+1)λ2
where n is an integer (0, 1, 2,...), and λ is the wavelength of light.
2. Choosing the Minimum Thickness:
To find the least thickness that eliminates reflection, we set n=0:
Δx=λ2
3. Calculating the Path Difference:
The path difference for light reflecting off the two interfaces (air-film and film-glass) is given by:
Δx=2t
where t is the thickness of the film.
4. Setting Up the Equation:
Equating the two expressions for path difference:
2t=λ2nfilm
where nfilm is the refractive index of the film (MgF₂).
5. Substituting Values:
Given:
- Wavelength λ=550nm=550×10−9m
- Refractive index of MgF₂ nfilm=1.38
We can substitute these values into the equation:
2t=550×10−92×1.38
6. Solving for Thickness t:
Rearranging gives:
t=550×10−94×1.38
Now calculating:
t=550×10−95.52≈99.64×10−9m=0.1μm
Final Answer:
The least coating thickness that eliminates reflection at the center of the visible spectrum is approximately 0.1μm.
---
For destructive interference to occur, the path difference between the two reflected rays must be an odd multiple of half wavelengths. The condition for destructive interference is given by:
Δx=(2n+1)λ2
where n is an integer (0, 1, 2,...), and λ is the wavelength of light.
To find the least thickness that eliminates reflection, we set n=0:
Δx=λ2
The path difference for light reflecting off the two interfaces (air-film and film-glass) is given by:
Δx=2t
where t is the thickness of the film.
Equating the two expressions for path difference:
2t=λ2nfilm
where nfilm is the refractive index of the film (MgF₂).
Given:
- Wavelength λ=550nm=550×10−9m
- Refractive index of MgF₂ nfilm=1.38
2t=550×10−92×1.38
Rearranging gives:
t=550×10−94×1.38
t=550×10−95.52≈99.64×10−9m=0.1μm
The least coating thickness that eliminates reflection at the center of the visible spectrum is approximately 0.1μm.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.57
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.58
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.55
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A glass lens is coated on one side with a thin film of magnesium fluoride (MgF2)to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of MgF2 is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm (λ=550nm)? Assume that the light is approxmately perpendicular to the lens surface.
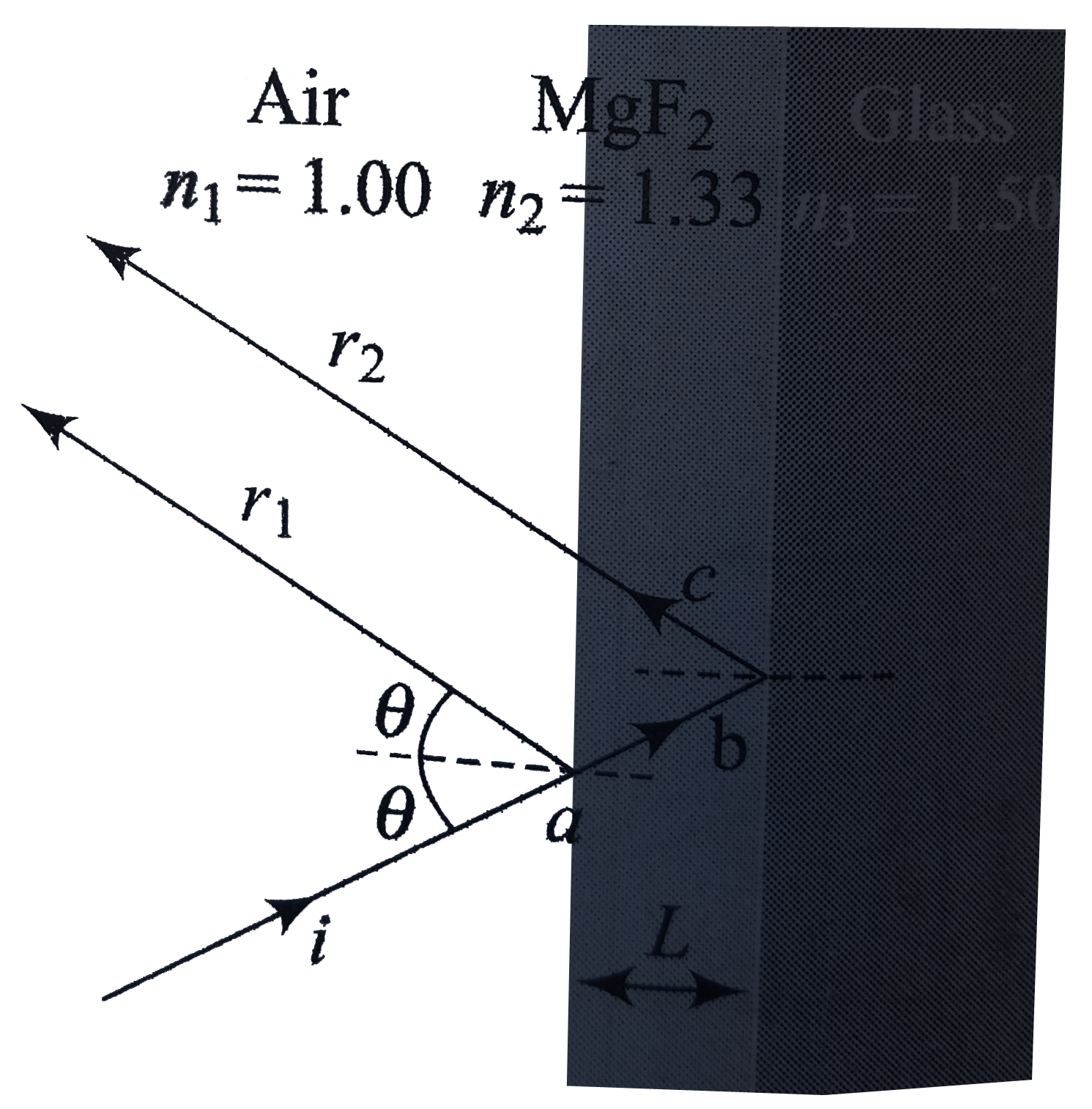
View SolutionIn solar cells, a silicon solar cell (μ=3.5) is coated with a thin film
of silicon monoxide SiO(μ=1.45) to minimize reflective losses from the surface.
Determine the minimum thickness of SiO that produces the least reflection at a
wavelength of 550nm, near the centre of the visible spectrum. Assume
approximately normal incidence .
View Solution
Knowledge Check
To ensure almost 100% transmittivity, photographic lenses are often coated with a thin layer of dielectric material, like MgF2(μ=1.38) . The minimum thickness of the film to be used so that at the centre of visible spectrum (λ=5500Å) there is maximum transmission.
A5000 Ã…B2000 Ã…C1000 Ã…D3000 Ã…
In solar cells, a silicon solar cell (μ=3.5) is coated with a thin film
of silicon monoxide SiO(μ=1.45) to minimize reflective losses from the surface.
Determine the minimum thickness of SiO that produces the least reflection at a
wavelength of 550nm, near the centre of the visible spectrum. Assume
approximately normal incidence .
View SolutionTo ensure almost 100% transmittivity, photographic lenses are often coated with a thin layer of dielectric material, like MgF2(μ=1.38) . The minimum thickness of the film to be used so that at the centre of visible spectrum (λ=5500Å) there is maximum transmission.
View SolutionA thin film with index of refraction 1.33 coats a glass lens with index of refraction 1.50. Which of the following choices is the smallest film thickness that will not reflect light with wavelength 640 nm?
View SolutionA double convex thin lens made of glass (refractive index μ=1.5) has both radii of curvature of magnitude 20 cm . Incident light rays parallel to the axis of the lens will converge at a distance L such that
View SolutionA double convex thin lens made of glass (refractive index μ=1.5) has both radii of curvature of magnitude 20 cm . Incident light rays parallel to the axis of the lens will converge at a distance L such that
View SolutionThe outer surface of a transparent glass slab of refractive index μS=1.5 is coated by a thin layer of transparent medium of refractive index μC=1.6. Orange light of wavelength 6400Å falls normally on the coating. The reflected light at the upper surface and at the lower surface of the coat interfere destructively. If thickness of the coat is 5K×10−8m, calculate the minimum value of K.
View SolutionWhat is the thinnest film of coating with n= 1.42 on glass (n=1.52) for which destructive interference of the red component (650 nm) of an incident white light beam in air can take place by reflection ?
View Solution
