A particle moves in a plane with a constant speed along a path y=2x2+3x−4 When the particle is at (0,-4) the direction along which it is moving is inclined to the X axis at an angle. Given tan−13=72∘
63∘
72∘
27∘
0∘
The correct Answer is:B
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the given path
The path of the particle is given by the equation:
y=2x2+3x−4
Step 2: Find the derivative of the path
To find the direction of the particle at a given point, we need to calculate the derivative dydx. This derivative represents the slope of the tangent to the curve at any point (x,y).
Differentiating the equation with respect to x:
dydx=ddx(2x2+3x−4)=4x+3
Step 3: Evaluate the derivative at the point (0, -4)
Now, we need to evaluate the derivative at the specific point where the particle is located, which is (0,−4).
Substituting x=0 into the derivative:
dydx∣∣∣(0,−4)=4(0)+3=3
Step 4: Relate the derivative to the angle
The slope of the tangent line at the point gives us the tangent of the angle θ that the direction of the particle makes with the x-axis. Therefore:
tanθ=3
Step 5: Find the angle θ
To find the angle θ, we take the arctangent (inverse tangent) of 3:
θ=tan−1(3)
Step 6: Use the given information
It is given in the problem that:
tan−1(3)=72∘
Thus, we conclude that:
θ=72∘
Final Answer
The direction along which the particle is moving is inclined to the x-axis at an angle of 72∘.
---
The path of the particle is given by the equation:
y=2x2+3x−4
To find the direction of the particle at a given point, we need to calculate the derivative dydx. This derivative represents the slope of the tangent to the curve at any point (x,y).
dydx=ddx(2x2+3x−4)=4x+3
Now, we need to evaluate the derivative at the specific point where the particle is located, which is (0,−4).
dydx∣∣∣(0,−4)=4(0)+3=3
The slope of the tangent line at the point gives us the tangent of the angle θ that the direction of the particle makes with the x-axis. Therefore:
tanθ=3
To find the angle θ, we take the arctangent (inverse tangent) of 3:
θ=tan−1(3)
It is given in the problem that:
tan−1(3)=72∘
Thus, we conclude that:
θ=72∘
The direction along which the particle is moving is inclined to the x-axis at an angle of 72∘.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.57
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.58
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.55
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A particle is moving with a constant speed along a straight line path. A force is not required to
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionA particle moves along the X-axis as x=u(t−2s)+a(t−2s)2.
View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle θ with x-axis.
View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle θ with x-axis.
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
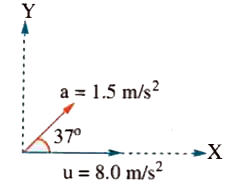
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View SolutionA particle moves along the X-axis as x=u(t−2s)=at(t−2)2.
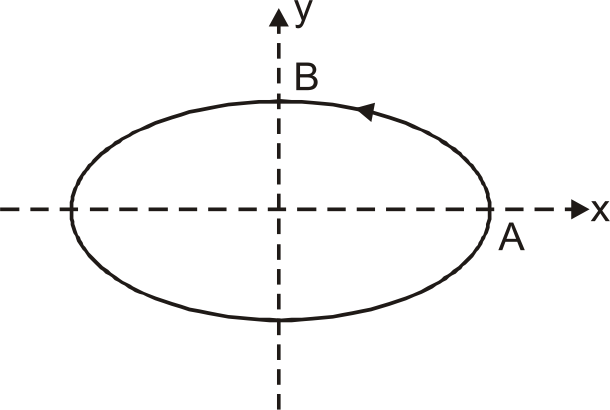
View SolutionA particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration :
View Solution
