A particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
To find the angular velocity of a particle moving with constant speed v along the x-axis about the point (0,b) when the particle is at the position (a,0), we can follow these steps:
Step 1: Identify the Position and Velocity
The particle is moving along the x-axis at position (a,0) with a constant speed v. The point about which we need to find the angular velocity is (0,b).
Step 2: Calculate the Distance r
To find the angular velocity, we first need to calculate the distance r between the point (0,b) and the particle's position (a,0). This can be calculated using the distance formula:
r=√(a−0)2+(0−b)2=√a2+b2
Step 3: Determine the Angle θ
Next, we need to find the angle θ between the line connecting the point (0,b) to the particle and the x-axis. The sine of this angle can be expressed as:
sinθ=br=b√a2+b2
Step 4: Find the Perpendicular Component of Velocity
The perpendicular component of the velocity v_{\perpendicular} to the line connecting the two points can be expressed as:
v_{\perpendicular} = v \sin \theta = v \cdot \frac{b}{\sqrt{a^2 + b^2}}
Step 5: Apply the Angular Velocity Formula
The angular velocity ω about the point (0,b) is given by the relationship:
\omega = \frac{v_{\perpendicular}}{r}
Substituting the values we found:
ω=v⋅b√a2+b2√a2+b2=vba2+b2
Final Answer
Thus, the angular velocity of the particle about the point (0,b) when the particle is at (a,0) is:
ω=vba2+b2
The particle is moving along the x-axis at position (a,0) with a constant speed v. The point about which we need to find the angular velocity is (0,b).
To find the angular velocity, we first need to calculate the distance r between the point (0,b) and the particle's position (a,0). This can be calculated using the distance formula:
r=√(a−0)2+(0−b)2=√a2+b2
Next, we need to find the angle θ between the line connecting the point (0,b) to the particle and the x-axis. The sine of this angle can be expressed as:
sinθ=br=b√a2+b2
The perpendicular component of the velocity v_{\perpendicular} to the line connecting the two points can be expressed as:
v_{\perpendicular} = v \sin \theta = v \cdot \frac{b}{\sqrt{a^2 + b^2}}
The angular velocity ω about the point (0,b) is given by the relationship:
\omega = \frac{v_{\perpendicular}}{r}
Substituting the values we found:
ω=v⋅b√a2+b2√a2+b2=vba2+b2
Thus, the angular velocity of the particle about the point (0,b) when the particle is at (a,0) is:
ω=vba2+b2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - J) Aakash Challengers Questions
13 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
A particle of mass m is moving with constant speed v on the line y=b in positive x-direction. Find its angular momentum about origin, when position coordinates of the particle are (a, b).
View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle θ with x-axis.
View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle θ with x-axis.
View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O

View SolutionA particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is

View SolutionA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
View SolutionA particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
View SolutionParticles AandB move with constant and equal speeds in a circle as shown in (Fig. 5.164). Find the angular velocity of the particle A with respect to B, if the angular velocity of particle Aw.r.t.O is ω.
 .
.
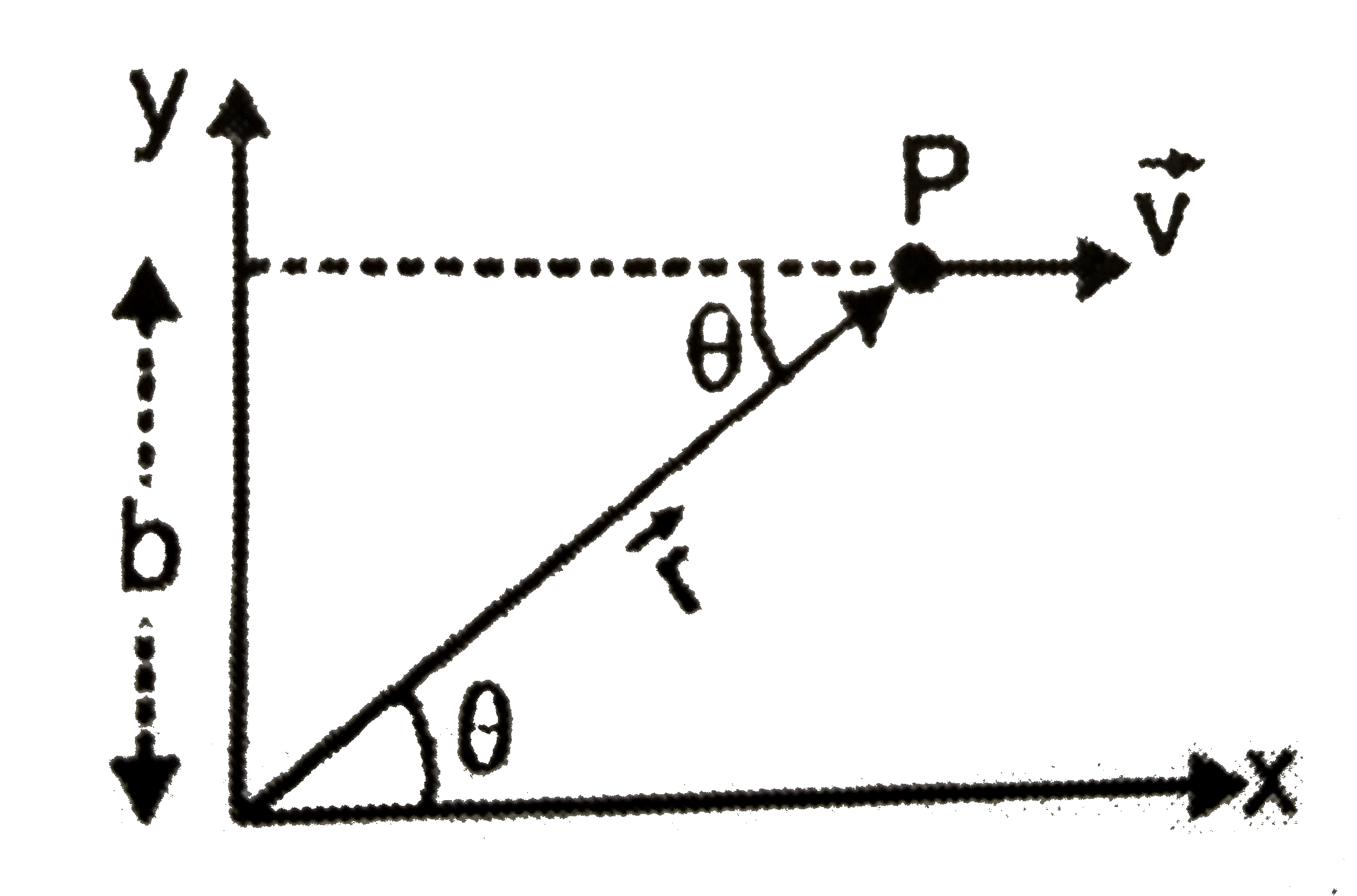
View SolutionA particle moving parallel to x-axis as shown in fig. such that at all instant the y-axis component of its position vector is constant and is equal to 'b'. Find the angular velocity of the particle about the origin when its radius vector makes angle θ from the axis.
View SolutionA particle is moving along x-direction with a constant acceleration a. The particle starts from x=x0 position with initial velocity u. We can define the position of the particle with time by the relation
x=x0+ut+12at2
plot the position of the particle in relation with time is following situations
(i) If initial position of the particle is on negativ x-axis, initial velocity is positive and acceleration is negative.
(ii) If initial position is positive, initial velocity is negative and acceleration is positive.
View Solution
