Figure shows elliptical path ‘abcd’ of a planet around the sun S such that the area of triangle ‘csa’ is 1/4 the area of the ellipse. (See figure) With ‘db’ as the major axis, and ‘ca’ as the minor axis. If t1 is the time taken for planet to go over path ‘abc’ and t2 for path taken over ‘cda’ then:
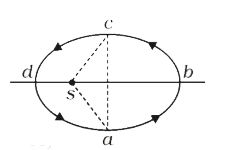
t1=3t2
t1=t2
t1=2t2
t1=4t2
The correct Answer is:A
Total area =A
Area of sabc=3AA
Area of sadc=A4
3A4t1=A4t2⇒t1=3t2
Related Playlists
Similar Questions
_E01_134_Q01.png)
Figure elliptical path abcd of a planet around the sun S such that the area of Delta csa is 14 the area of the ellipse, (see figure) with db as the semimajor axis, and ca as the semiminor axis if t1 is the time taken for planet to go over path abc and t2 for path taken over cda then:View SolutionFigure shows the elipticla path of a planet about the sun. The two shaded parts have equal area. If t1andt2 be the tim taken by the planet to go from a to b and from c to d respectively
View Solution_S01_025_Q01.png)
The figure shows elliptical orbit of a planet m about the sun S. the shaded area SCD is twice the shaded area SAB. If t1 be the time for the planet to move from C to D and t2 is the time to move from A to B, then:View Solution_S01_025_Q01.png)
The figure shows elliptical orbit of a planet m about the sun S. the shaded area SCD is twice the shaded area SAB. If t1 be the time for the planet to move from C to D and t2 is the time to move from A to B, then:View SolutionFigure shows the motion of a planet around the Sun S in an elliptical orbit with the Sun at the focus. The shaded areas A and B are also shown in the figure which can be assumed to be equal. If t1 and t2 represent the time taken for the planet to move from a to b and c to d, respectively then
 View Solution
View SolutionFigure shows the motion of a planet around the Sun S in an elliptical orbit with the Sun at the focus. The shaded areas A and B are also shown in the figure which can be assumed to be equal. If t1 and t2 represent the time taken for the planet to move from a to b and c to d, respectively then
 View Solution
View SolutionThe figure shows elliptical orbit of a plant P about the sun S. The shaded area CSD is twice tha shaded area ASB. If t1 is the time taken by the planet to move from C to D and t2 is the time to move from A to B, determine the ratio t1/t2
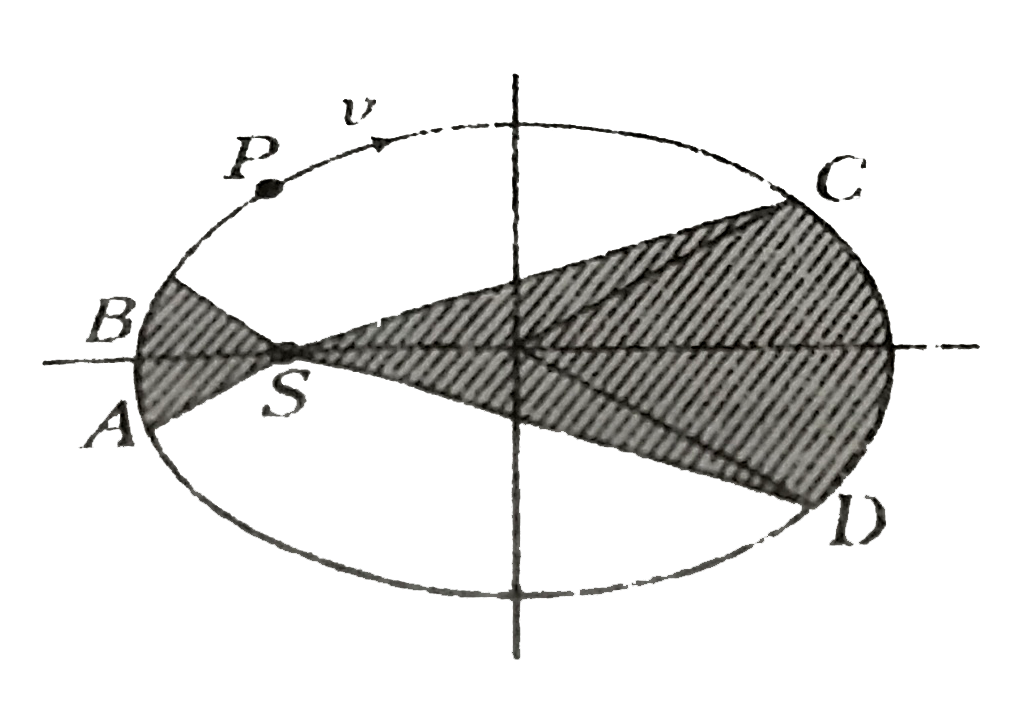 View Solution
View SolutionThe figure represents an elliptical orbit a planet around sun. The planet takes time T1 to travel from A to B and it takes time T2 to travel from C to D. If the area CSD is double that of area ASB, them
 View Solution
View SolutionA planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the ends of the minor axis and major axis close to the sun is
View SolutionFigure 1.31 shows the trace of the path of a charged particle in a bubble chamber. Assume that the magnetic field is into the plane of the paper with magnitude 0.4 T. The smooth spiral path occurs because the particle loses energy in ionizing molecules along the path.
a. Which part of the path corresponds to higher kinetic energy for the particle? Inner or outer part of spiral.
b. Is the charge positive or negative?
c. The radius of curvature ranges from 70 mm to 10 mm. What is the range of values of the magnitude of momentum if the magnitude of the charge is e?
 View Solution
View Solution


