If two glass plates have water between them and are separated by very small distance (see figure). It is very difficult to pull them apart. It is because the water in between forms cylindrical surface on the side that gives rise ot lower pressure in the water in comparison to atmosphere. If the radius of the cylindrical surface is R and surface tension of water is T then the pressure in water between the plates is lowr by: 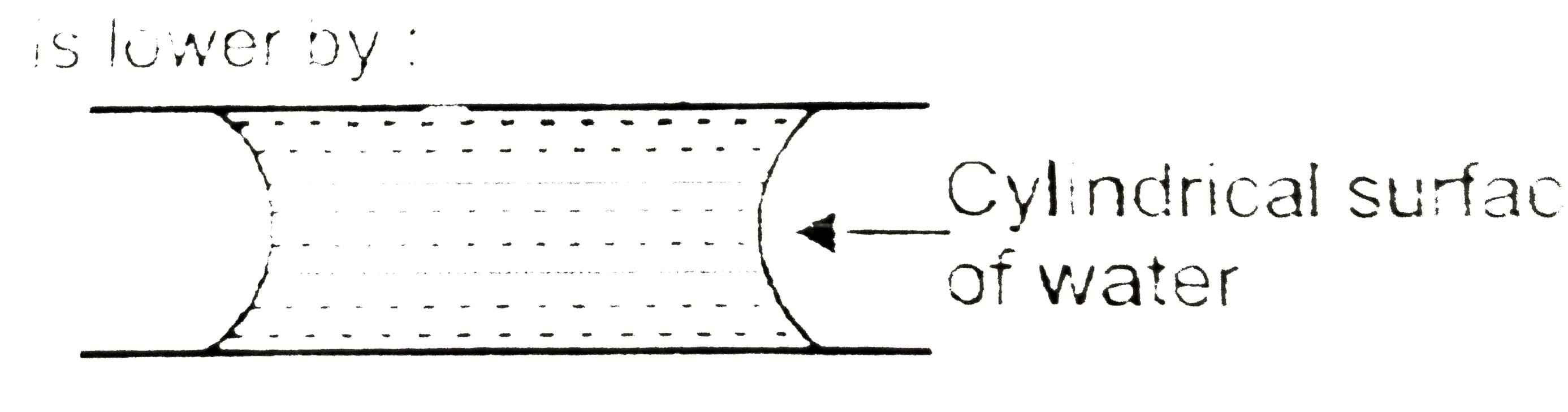
2TR
TR
T4R
4TR
The correct Answer is:B
Excess pressure =T[1r1+1r2]
=Tr∵(r1=Rr2→∞)
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
On increasing temperature , surface tension of water
View SolutionOn mixing the salt in water, the surface tension of water will
View SolutionIf a detergent is dissolved in water, the surface tension of water
View SolutionThe force required to lift a circular flat plate of radius 5 cm on the surface of water is: (Surface tension of water is 75 dyne/cm):-
View SolutionA water tank is 20 m deep . If the water barometer reads 10 m at the surface , then what is the pressure at the bottom of the tank in atmosphere ?
View SolutionSurface tension of water is 0.072 Nm−1. The excess pressure inside a water drop of diameter 1.2 mm is :-
View SolutionCalculate the force required to take away a flat circular plate of radius 0.02m from the surface of water. The surface tension of water is 0.07Nm−1
View SolutionAn air bubble of radius r in water is at a depth h below the water surface at some instant. If P is atmospheric pressure, d and T are density and surface tension of water respectively . the pressure inside the bubble will be :
View SolutionA spherical air bubble is formed in water at a depth of 1.2 m from the surface. The diameter of the bubble is 0.6 mm and surface tension of water is 0.073Nm−1. Calculate the pressure inside . Atmospheric pressure =10.3m of water.
View SolutionA spherical drop of water has 1mm radius. If the surface tension of water is 70×10−3N/m, then the difference of pressure between inside and outside of the spherical drop is:
View Solution
