x and y displacements of a particle are given as x(t)=−asinωt and y(t)=asin2ωt. Its trajectory will look like.
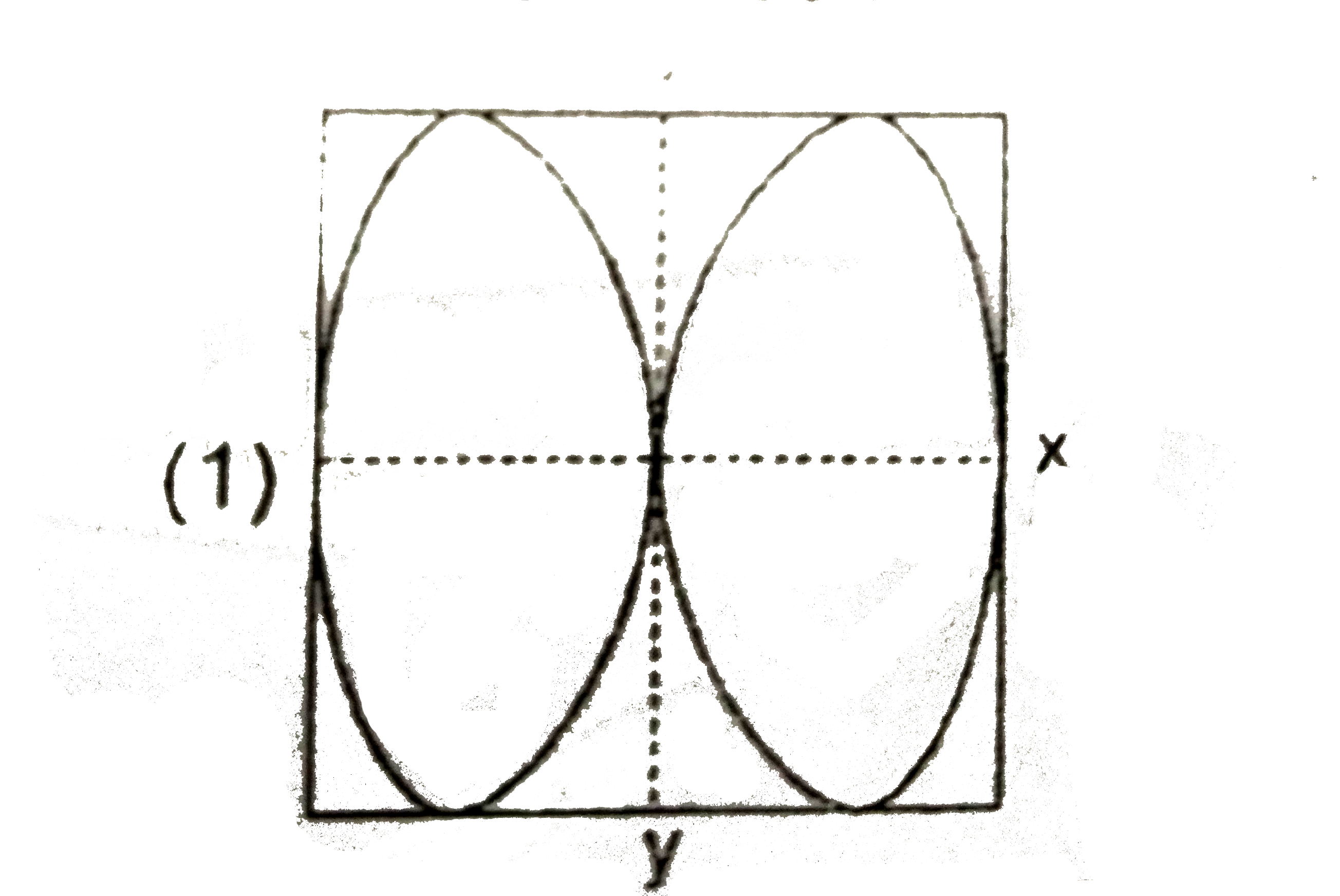
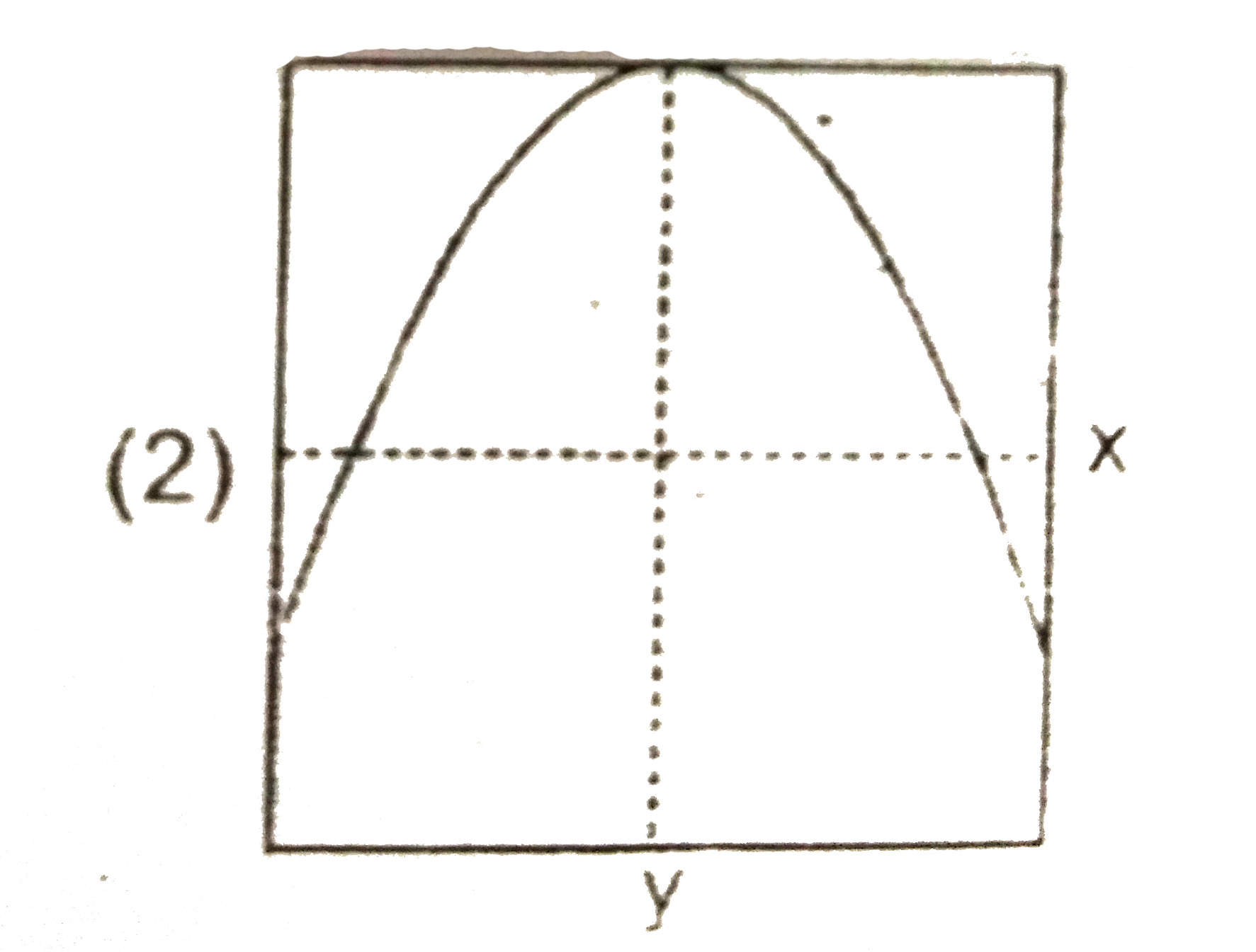
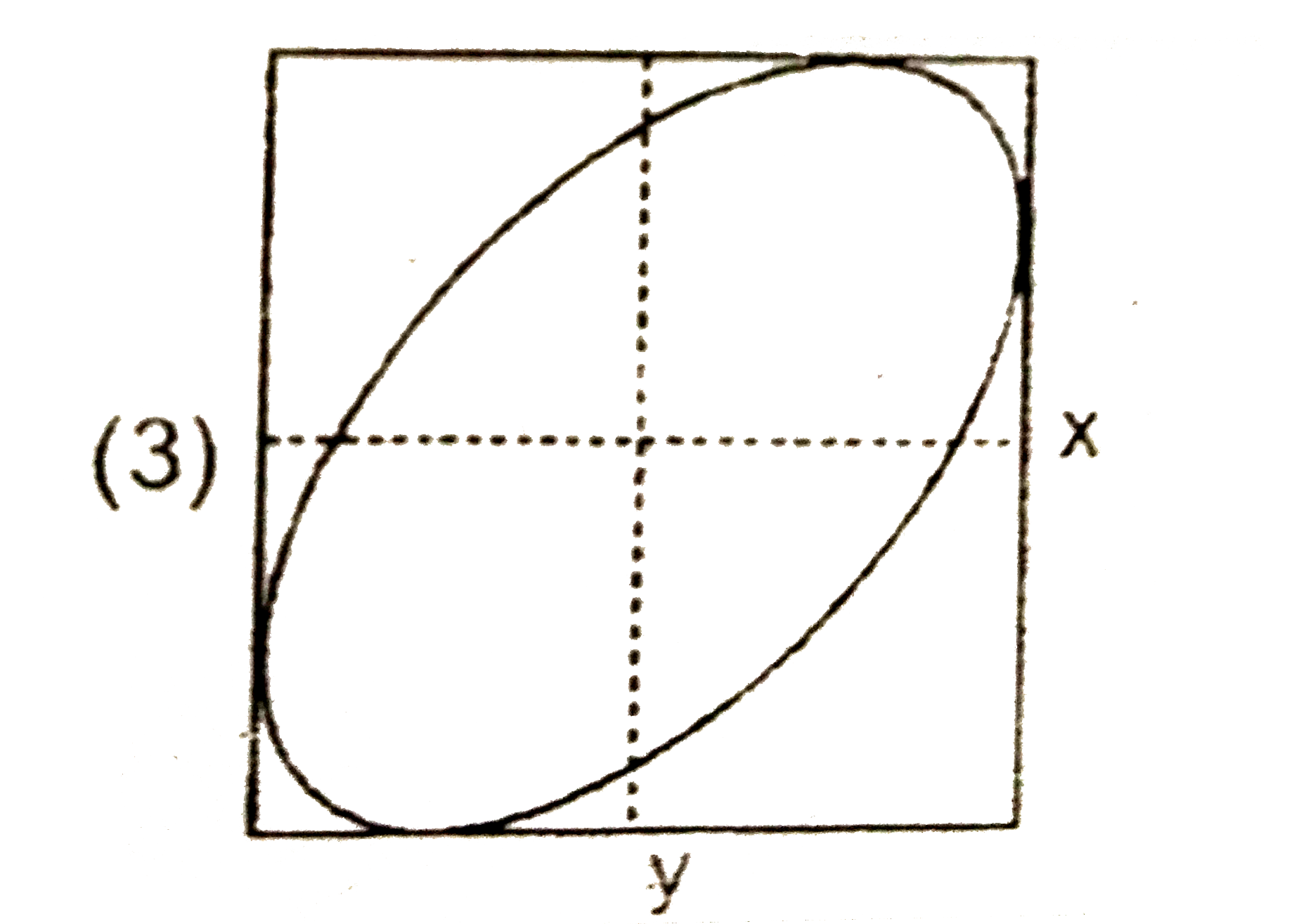
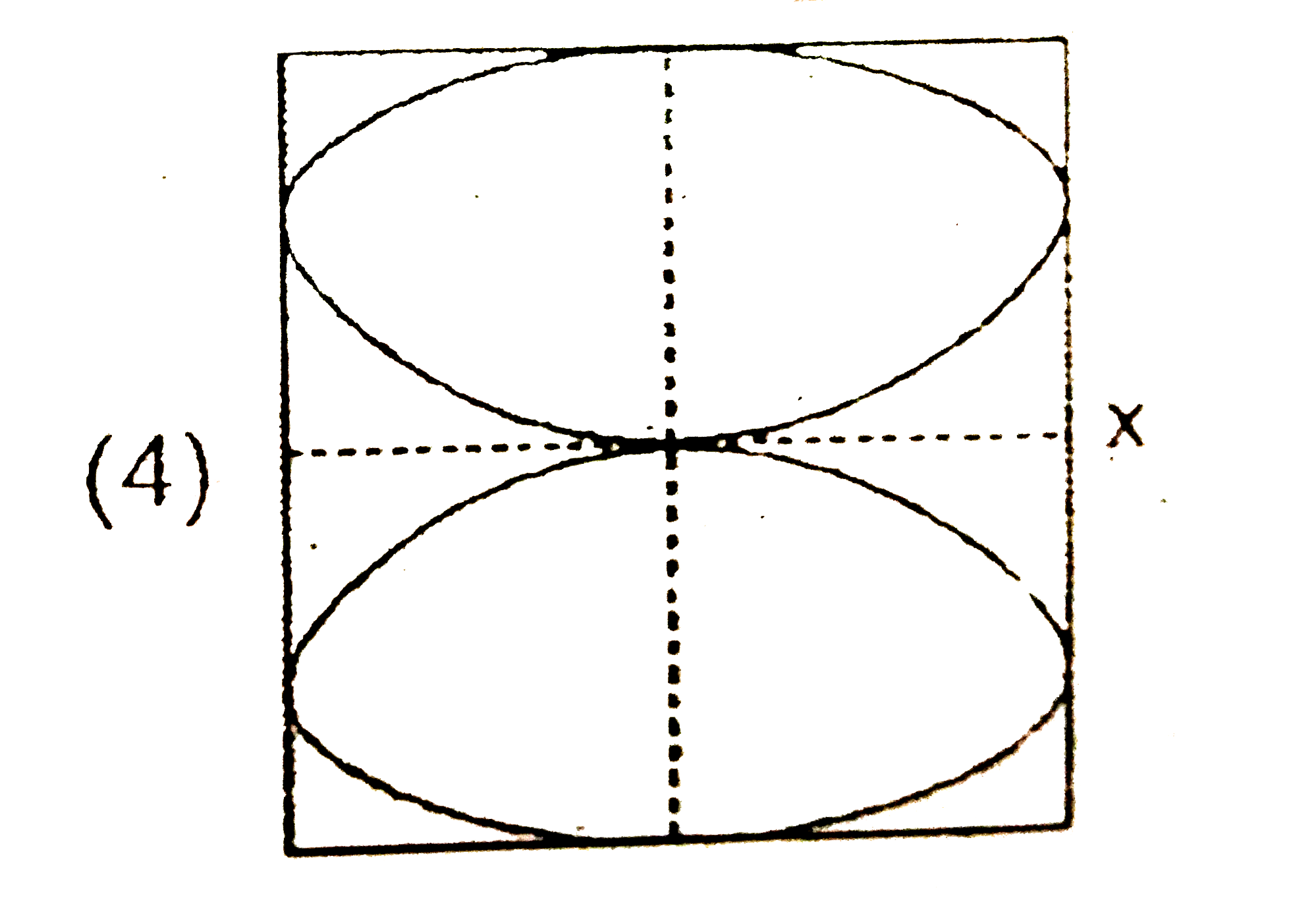
The correct Answer is:A
To solve the problem, we need to analyze the given equations for the displacements x(t) and y(t):
1. Given Equations:
x(t)=−asin(ωt)
y(t)=asin(2ωt)
2. Finding Points on the Trajectory:
- We will evaluate the trajectory at specific time intervals to understand how x and y change.
3. At t=0:
x(0)=−asin(0)=0
y(0)=asin(0)=0
- So, the particle starts at the origin (0,0).
4. At t=π2ω:
x(π2ω)=−asin(ω⋅π2ω)=−asin(π2)=−a
y(π2ω)=asin(2ω⋅π2ω)=asin(π)=0
- At this point, the particle is at (−a,0).
5. At t=π4ω:
x(π4ω)=−asin(π4)=−a⋅√22=−a√22
y(π4ω)=asin(π2)=a
- The particle is at (−a√22,a).
6. At t=πω:
x(πω)=−asin(π)=0
y(πω)=asin(2π)=0
- The particle returns to the origin (0,0).
7. At t=3π4ω:
x(3π4ω)=−asin(3π4)=−a⋅√22=−a√22
y(3π4ω)=asin(3π2)=−a
- The particle is at (−a√22,−a).
8. At t=3π2ω:
x(3π2ω)=−asin(3π2)=a
y(3π2ω)=asin(3π)=0
- The particle is at (a,0).
9. At t=2π/ω:
x(2π/ω)=−asin(2π)=0
y(2π/ω)=asin(4π)=0
- The particle returns to the origin (0,0).
10. Conclusion:
- The trajectory of the particle will form a closed loop, oscillating between the points (−a,0), (0,a), (a,0), and (0,−a). The shape of the trajectory is a vertical ellipse.
x(t)=−asin(ωt)
y(t)=asin(2ωt)
- We will evaluate the trajectory at specific time intervals to understand how x and y change.
x(0)=−asin(0)=0
y(0)=asin(0)=0
- So, the particle starts at the origin (0,0).
x(π2ω)=−asin(ω⋅π2ω)=−asin(π2)=−a
y(π2ω)=asin(2ω⋅π2ω)=asin(π)=0
- At this point, the particle is at (−a,0).
x(π4ω)=−asin(π4)=−a⋅√22=−a√22
y(π4ω)=asin(π2)=a
- The particle is at (−a√22,a).
x(πω)=−asin(π)=0
y(πω)=asin(2π)=0
- The particle returns to the origin (0,0).
x(3π4ω)=−asin(3π4)=−a⋅√22=−a√22
y(3π4ω)=asin(3π2)=−a
- The particle is at (−a√22,−a).
x(3π2ω)=−asin(3π2)=a
y(3π2ω)=asin(3π)=0
- The particle is at (a,0).
x(2π/ω)=−asin(2π)=0
y(2π/ω)=asin(4π)=0
- The particle returns to the origin (0,0).
- The trajectory of the particle will form a closed loop, oscillating between the points (−a,0), (0,a), (a,0), and (0,−a). The shape of the trajectory is a vertical ellipse.
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 106 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
Similar Questions
Knowledge Check
The displacement of a particle varies with time according to the relation y=asinωt+bcosωt.
AThe motion is oscillatory but not SHM.BThe motion is SHM with amplitude a+b.CThe motion is SHM with amplitude a2+b2DThe motion is SHM with amplitude √a2+b2.A particle is acted simultaneously by mutually perpendicular simple harmonic motions x=a cosωt and y=asinωt. The trajectory of motion of the particle will be
Aan ellipseBa parabolaCa circleDa straight line.
A xandy co-ordinates of a particle are x=Asin(ωt)andy=Asin(ωt+π/2). Then, the motion of the particle is

View SolutionA particle is acted simultaneously by mutally perpendicular simple harmonic motion x=acosωt and y=asinωt. The trajectory of motion of the particle will be
View SolutionThe displacement of a particle along the x- axis it given by x=asin2ωt The motion of the particle corresponds to
View SolutionThe displacement of a particle along the x-axis is given by x=asin2ωt. The motion of the particle corresponds to
View SolutionIf the displacement of a particle varies with time as x=5t2+7t.
Then find its velocity.
View SolutionThe horizontal and vertical displacements of a particle moving along a curved line are given by x=5tandy=2t2+t. Time after which its velocity vector makes an angle of 45∘ with the horizontal is
View Solution

