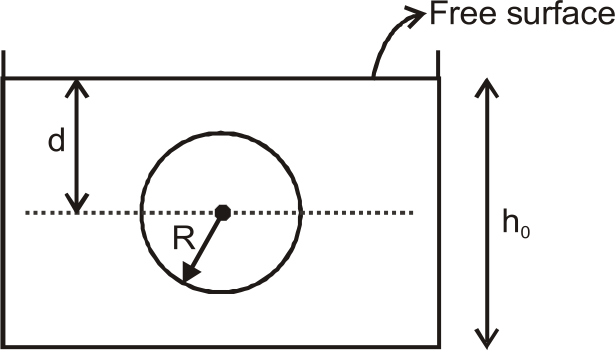
A uniform solid sphere of radius R is in equilibrium inside a liquid whose density varies with depth from free surface as ρ=ρ0(1+hh0) where h is depth from free surface. Density of sphere σ will be :
σ=ρ0(1+d2h0)
σ=ρ0(1−d2h0)
σ=ρ0(1+2dh0)
σ=ρ0(1+dh0)
dB=π(R2−y2)dyρ0(1+d−yh0)g
dB=πρ0gh0(R2−y2)(h0+d−y)dy
=πρ0gh0[R2(h0+d)dy−R2ydy−(h0+d)y2dy+y3dy]
B=∫+Ry=−RdB=πρ0gh0(R2(h0+d)y−R2y22−(h0+d)y33+y44)+R−R
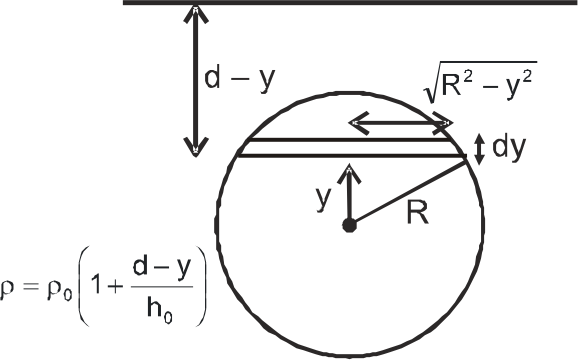
B=πρ0gh0[(h0+d)R2(2R)−(h0+d)3(2R3)]=πρ0gh0[43(h0+d)R3]
=43πR3g(ρ0)h0(h0+d)=43πR3gσ⇒σ=ρ0h0(h0+d)
σ=ρ0(1+dh0)
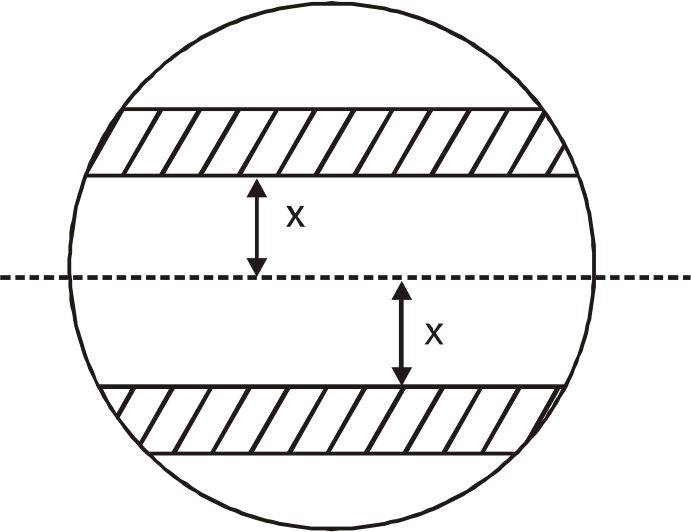
Alternate solution
σvg=∫[ρ0(1+d−xh0)dvg+ρ0(1+d+xh0)dvg]
σv=2ρ0(1+dh0)∫v/20dV=ρ0v(1+dv0)
⇒σ=ρ0(1+dh0)
Topper's Solved these Questions
Similar Questions
A small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.

Where will the ball come in the equilibrium?
View SolutionA small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.

The motion of the ball in the vessel is
View Solution
Knowledge Check
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ
A small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.

The ball will reach at the bottom of the vessel
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionDensity of a liquid varies with depth as ρ=αh. A small ball of density ρ0 is released from the free surface of the liquid. Then
View SolutionA small ball of density rho_(0) is released from the surface of a liquid whose density varies with depth h as ρ=ρ02(α+βh). Mass of the ball is m. Select the most appropriate one option.
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View Solution
