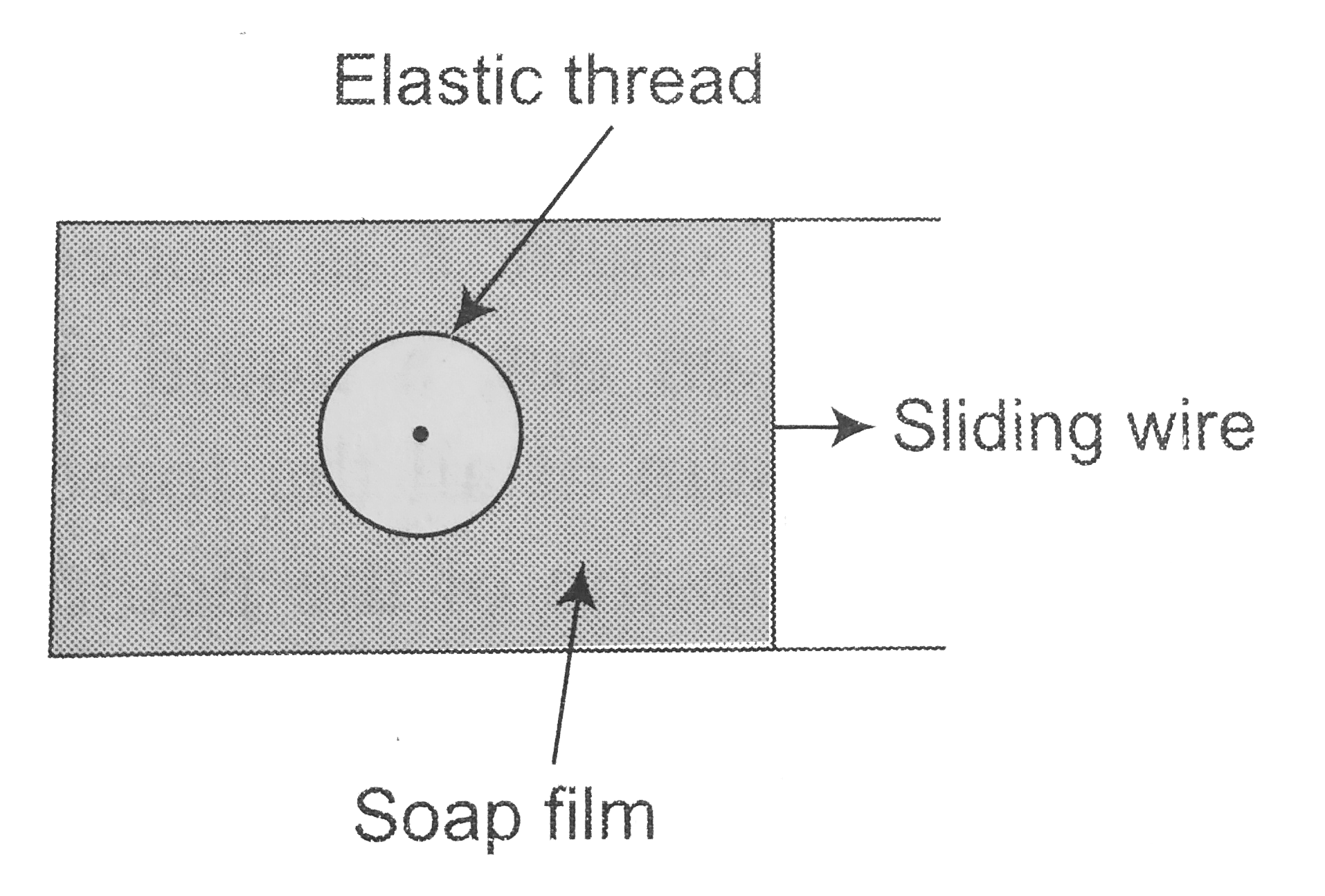
The figure shows a soap film in which a closed elastic thread is lying. The film inside the thread is pricked. Now the sliding wire is moved out so that the surface area increases. The radius circle of the circle formed by elastic thread will
increases
decreases
remains same
data insufficient
The force exerted by film on wire or thread depends only on the nature of material of the film and not on its surface area. Hence the radius of circle formed by elastic thread does not change.
Topper's Solved these Questions
Similar Questions
A wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030Nm−1.
View SolutionA wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030Nm−1.
View SolutionA thin and light thread of sufficient length L is attached to a wire frame. The frame (along with the thread) is dipped into soap solution. When the frame is taken out of the solution, the thread takes the form of a semicircle with a soap film extending between the frame and the thread as shown in the figure (a). Now the thread is deformed into two semicircles by applying a force of F at the middle of the thread, as a result the film gets strectched as shown in the figure. (b). Calculate the surface tension of the soap solution.

View SolutionA film of soap solution is formed on a loop frame loop of 6.28cm long thread is gently put on the film and the film is broken with a needle inside the loop. The tread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030n/m.
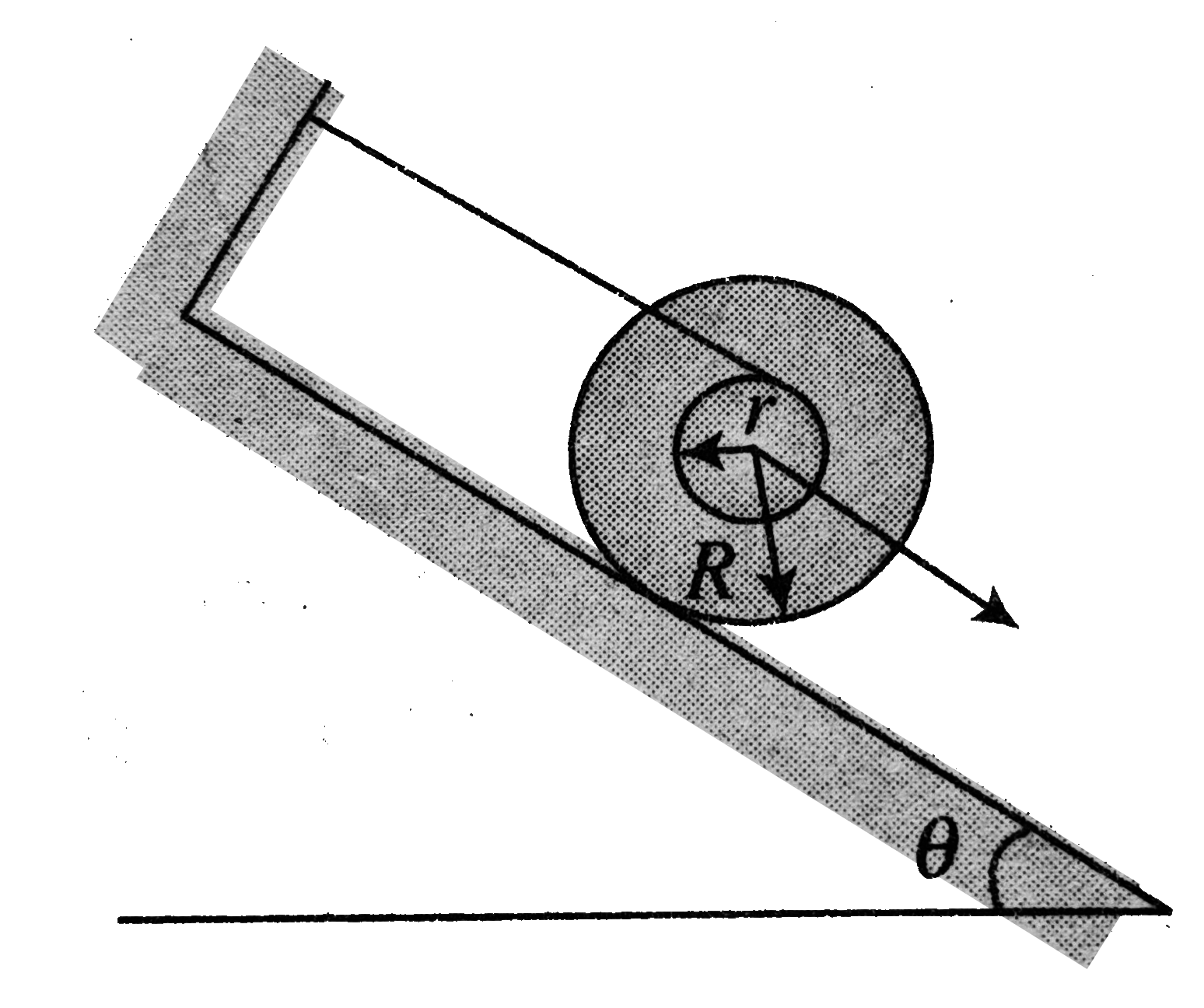
View SolutionFigure shows a spool with thread wound on it placed on a smooth plane inclined at angle from horizontal. The spool has mass m, edge radius R, and is wound up to a radius r. its moment of inertia about its own axis is I. The free end of the thread is attached as shown in the figure. So that the thread is parallel to the inclined plane. T is the tension in the thread. Which of the following is correct?
View SolutionThere is a horizontal film of soap solution. On it a thread is placed in the form of a loop. The film is pierced inside the loop and the thread becomes a circular loop of radius R. If the surface tension of the loop be T, then what will be the tension in the thread?
View SolutionA wire of length 2 units is cut into two parts which are bent respectively to form a square of side = x units and a cricle of radius = r units. If the sum of areas of the square and the circle so formed is minimum, then
View Solution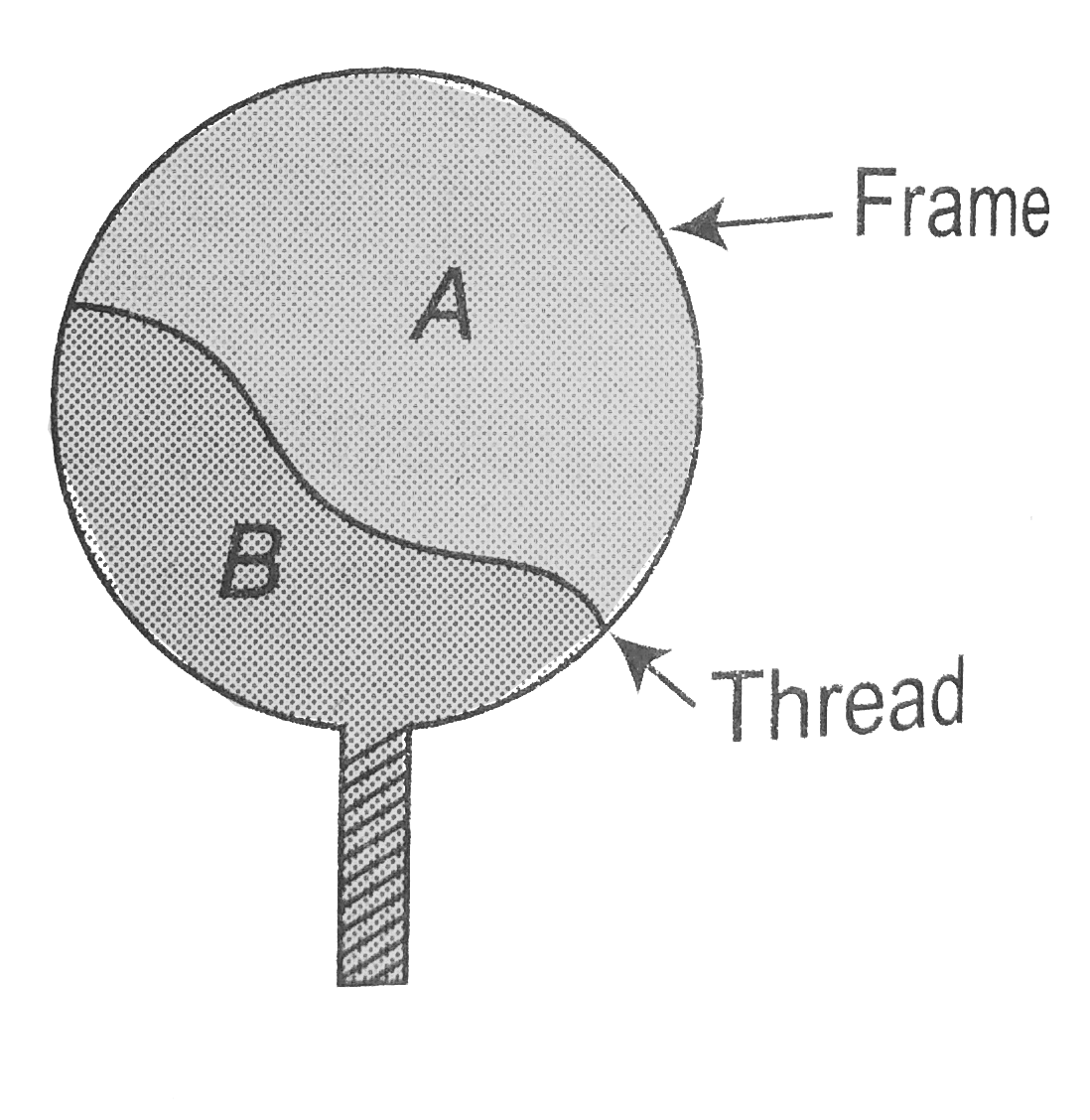
A thread is tied slightly loose to a wire frame as in figure and the frame is dipped into a soap solution and taken out . The frame is comletely covered with the film. When the portion A puntured with a pin The thread.
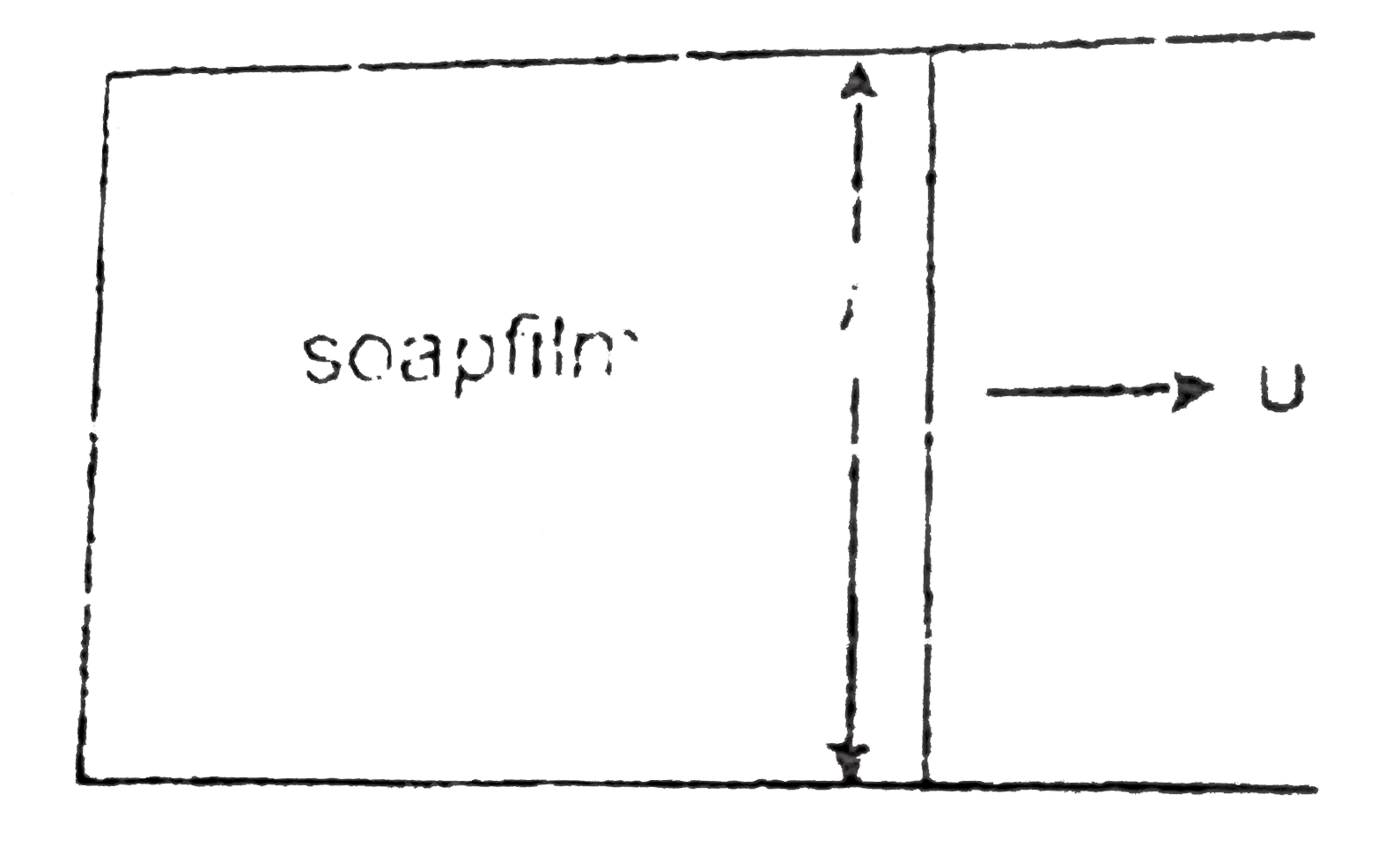
View SolutionA soap film is created in a small wire frame as shown in the figure. The sliding wire of mass m is given a velocity u to the right and assume that u is small enough so that film does not break. Plane of the film is horizontal and surface tension is T, then time to region the original position of wire is equal to :
View SolutionShows a rod PQ of length 20.0 cm and mass 200g suspended through a fixed point O by two threads of lengths 20.0 cm each. A magnetic field of strenght 0.500 T exists in the vicinity of the wire PQ as shown in the figure. The exists in the vicinity of the wire PQ as shown in the figure. The wires conecting PQ with the battery are loose and exert no force on PQ.(a) find the tension in the threads when the switch S is open. (b) A current of 2.0 A is established when the switch S is closed. Find the tension in the threads now.

View Solution

