A wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030Nm−1.
The correct Answer is:A, C, D
To solve the problem, we will follow these steps:
Step 1: Understand the problem
We have a loop of thread that is placed on a soap film. The length of the thread is given as 6.28 cm, and the surface tension of the soap solution is given as 0.030 N/m. The thread takes the shape of a circle when the film is pricked.
Step 2: Convert the length of the thread to meters
The length of the thread is given in centimeters, so we need to convert it to meters for consistency in units.
L=6.28cm=6.28×10−2m
Step 3: Relate the length of the thread to the radius of the circle
The length of the thread (L) is equal to the circumference of the circle formed by the thread. The formula for the circumference of a circle is:
L=2πr
where r is the radius of the circle. We can rearrange this to find the radius:
r=L2π
Step 4: Calculate the radius
Substituting the value of L:
r=6.28×10−22π=6.28×10−22×3.14=1×10−2m=0.01m
Step 5: Understand the forces acting on the thread
When the film is pricked, the surface tension acts along the edges of the film. The total upward force due to surface tension is balanced by the tension in the thread. The upward force due to surface tension can be expressed as:
Force due to surface tension=Surface Tension×Length of the film
Since the film has two surfaces (top and bottom), the effective length is 2r:
Force due to surface tension=S×2r
Step 6: Set up the equation for tension
The tension T in the thread must balance the force due to surface tension:
2T=S×2r
This simplifies to:
T=S×r
Step 7: Substitute the values to find tension
Now we can substitute the values of surface tension S=0.030N/m and radius r=0.01m:
T=0.030×0.01=0.0003N=3.0×10−4N
Final Answer
The tension in the thread is:
3.0×10−4N
We have a loop of thread that is placed on a soap film. The length of the thread is given as 6.28 cm, and the surface tension of the soap solution is given as 0.030 N/m. The thread takes the shape of a circle when the film is pricked.
The length of the thread is given in centimeters, so we need to convert it to meters for consistency in units.
L=6.28cm=6.28×10−2m
The length of the thread (L) is equal to the circumference of the circle formed by the thread. The formula for the circumference of a circle is:
L=2πr
where r is the radius of the circle. We can rearrange this to find the radius:
r=L2π
Substituting the value of L:
r=6.28×10−22π=6.28×10−22×3.14=1×10−2m=0.01m
When the film is pricked, the surface tension acts along the edges of the film. The total upward force due to surface tension is balanced by the tension in the thread. The upward force due to surface tension can be expressed as:
Force due to surface tension=Surface Tension×Length of the film
Since the film has two surfaces (top and bottom), the effective length is 2r:
Force due to surface tension=S×2r
The tension T in the thread must balance the force due to surface tension:
2T=S×2r
This simplifies to:
T=S×r
Now we can substitute the values of surface tension S=0.030N/m and radius r=0.01m:
T=0.030×0.01=0.0003N=3.0×10−4N
The tension in the thread is:
3.0×10−4N
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.1
1 Video
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.2
1 Video
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based
7 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A film of soap solution is formed on a loop frame loop of 6.28cm long thread is gently put on the film and the film is broken with a needle inside the loop. The tread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030n/m.
View SolutionThere is a horizontal film of soap solution. On it a thread is placed in the form of a loop. The film is pierced inside the loop and the thread becomes a circular loop of radius R. If the surface tension of the loop be T, then what will be the tension in the thread?
View SolutionA 0.02 cm liquid column balances the excess pressure inside a soap bubble of radius 7.5 mm. Determine the density of the liquid. Surface tension of soap solution 0.03Nm−1.
View SolutionWork done in increasing the size of a soap bubble from a radius of 3cm to 5cm is nearly (Surface tension of soap solution =0.03Nm−1)
View Solution0.04 cm liquid column balances the excess pressure inside a soap bubble of radius 6 mm. Evaluate density of the liquid. Surface tension of soap solurtion =0.03Nm−1.
View Solution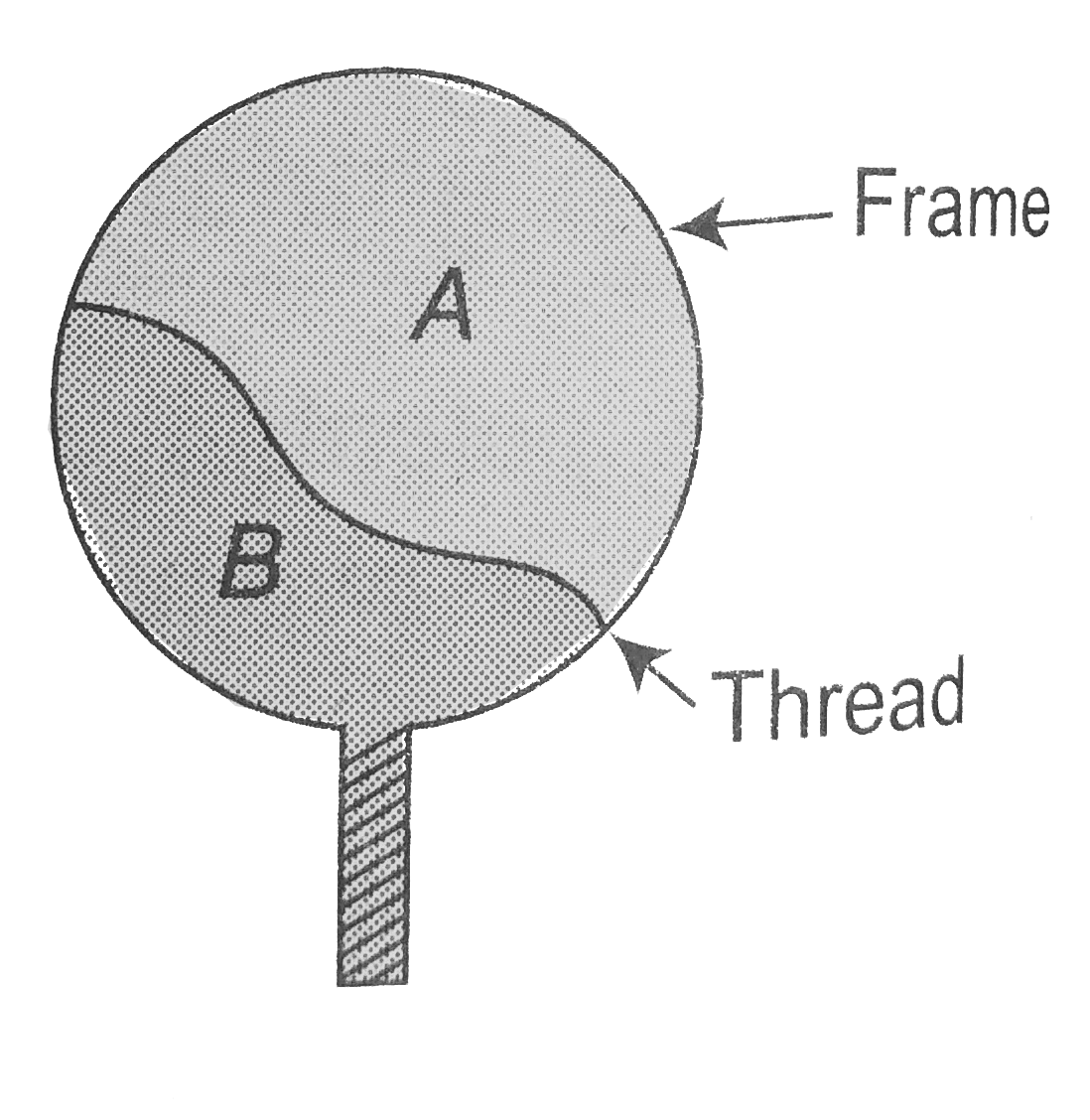
A thread is tied slightly loose to a wire frame as in figure and the frame is dipped into a soap solution and taken out . The frame is comletely covered with the film. When the portion A puntured with a pin The thread.
View SolutionA 5.0 cm long straight piece of thread is kept on the surface of water. Find the force with which the surface on one side of the thread pulls it. Surface tension of water =0.076Nm−1
View SolutionFind the difference of pressure between inside and outside of a soap bubble 5mm in diameter . Surface tension of soap solution is 3.2×10−2Nm−1
View SolutionWork done in increasing the size of a soap bubble from a radius of 3cm to 5cm is nearly. (surface tension of soap solution =0.3Nm−1)
View SolutionHow much work will be done in increasing the diameter of a soap bubble from 2 cm to 5 cm. Surface tension of soap solution is 3.0×10−2Nm−1.
View Solution
