A spring is attached to the bottom of an swimming pool, with the axis of the spring oriented vertically. An 8.00 kg block of wood (ρ=840kh/m3) is fixed to the top of the spring and compressed it. Then the pool is filled with water, completely covering the block. the spring is now observed to be stretched twice as much as it had been conpressed. Determine the percentage of the block's total volume that is hollow. Ignore any air in the hollow space.
The correct Answer is:A, D
To solve the problem step by step, we need to analyze the forces acting on the block of wood when it is submerged in water and how the spring behaves under these conditions.
Step 1: Understand the initial compression of the spring
When the block of wood is placed on the spring and compressed by a distance x, the force exerted by the spring is given by Hooke's Law:
Fspring=kx
where k is the spring constant. At this point, the spring force balances the weight of the block:
kx=mg
where m=8.00kg and g=9.81m/s2.
Step 2: Analyze the situation when the spring is stretched
When the pool is filled with water and the spring is stretched to a distance 2x, the forces acting on the block include the buoyant force from the water and the weight of the block. The net force on the block can be expressed as:
F=mg+Fspring=mg+k(2x)
The buoyant force Fbuoyant acting on the block is equal to the weight of the water displaced by the block, which can be expressed as:
Fbuoyant=ρwaterVblockg
where ρwater is the density of water (approximately 1000kg/m3) and Vblock is the volume of the block.
Step 3: Set up the equation for the stretched spring
At the stretched position, we can write:
Fbuoyant=mg+k(2x)
Substituting the expression for buoyant force:
ρwaterVblockg=mg+k(2x)
Step 4: Relate the two scenarios
From the first scenario, we know:
kx=mg
Thus, we can substitute kx in the second equation:
ρwaterVblockg=mg+2mg=3mg
This simplifies to:
ρwaterVblockg=3mg
Step 5: Solve for the volume of the block
Rearranging gives:
Vblock=3mgρwaterg=3mρwater
Substituting m=8.00kg and ρwater=1000kg/m3:
Vblock=3×8.001000=0.024m3
Step 6: Calculate the volume of the wood
The volume of the wood can be calculated using its density:
Vwood=mρwood=8.00840≈0.00952m3
Step 7: Calculate the volume of the hollow space
The volume of the hollow space Vhollow is given by:
Vhollow=Vblock−Vwood=0.024−0.00952=0.01448m3
Step 8: Calculate the percentage of the block's total volume that is hollow
The percentage of the block's total volume that is hollow can be calculated as:
Percentage of hollow volume=(VhollowVblock)×100=(0.014480.024)×100≈60.33%
Final Answer
The percentage of the block's total volume that is hollow is approximately 60.33%.
When the block of wood is placed on the spring and compressed by a distance x, the force exerted by the spring is given by Hooke's Law:
Fspring=kx
where k is the spring constant. At this point, the spring force balances the weight of the block:
kx=mg
where m=8.00kg and g=9.81m/s2.
When the pool is filled with water and the spring is stretched to a distance 2x, the forces acting on the block include the buoyant force from the water and the weight of the block. The net force on the block can be expressed as:
F=mg+Fspring=mg+k(2x)
The buoyant force Fbuoyant acting on the block is equal to the weight of the water displaced by the block, which can be expressed as:
Fbuoyant=ρwaterVblockg
where ρwater is the density of water (approximately 1000kg/m3) and Vblock is the volume of the block.
At the stretched position, we can write:
Fbuoyant=mg+k(2x)
Substituting the expression for buoyant force:
ρwaterVblockg=mg+k(2x)
From the first scenario, we know:
kx=mg
Thus, we can substitute kx in the second equation:
ρwaterVblockg=mg+2mg=3mg
This simplifies to:
ρwaterVblockg=3mg
Rearranging gives:
Vblock=3mgρwaterg=3mρwater
Substituting m=8.00kg and ρwater=1000kg/m3:
Vblock=3×8.001000=0.024m3
The volume of the wood can be calculated using its density:
Vwood=mρwood=8.00840≈0.00952m3
The volume of the hollow space Vhollow is given by:
Vhollow=Vblock−Vwood=0.024−0.00952=0.01448m3
The percentage of the block's total volume that is hollow can be calculated as:
Percentage of hollow volume=(VhollowVblock)×100=(0.014480.024)×100≈60.33%
The percentage of the block's total volume that is hollow is approximately 60.33%.
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Example 13.1
Explore 1 Video
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Example 13.2
Explore 1 Video
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Level 2 Comprehension Based
Explore 7 Videos
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
A block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionThe spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
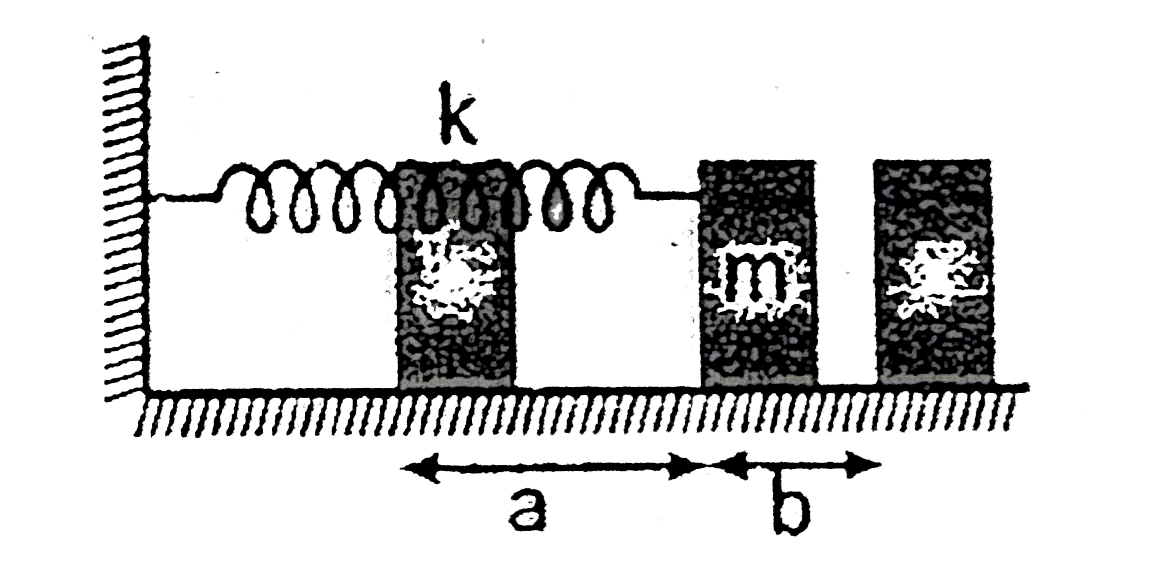
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View SolutionIn the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be

View Solution
A block of mass m is suspended from a spring and executes vertical SHM of time period T as shown in Fig. The amplitude of the SHM is A and spring is never in compressed state during the oscillation. The magnitude of minimum force exerted by spring on the block is
View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is

View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is

View SolutionA block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is

View SolutionA block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View Solution
