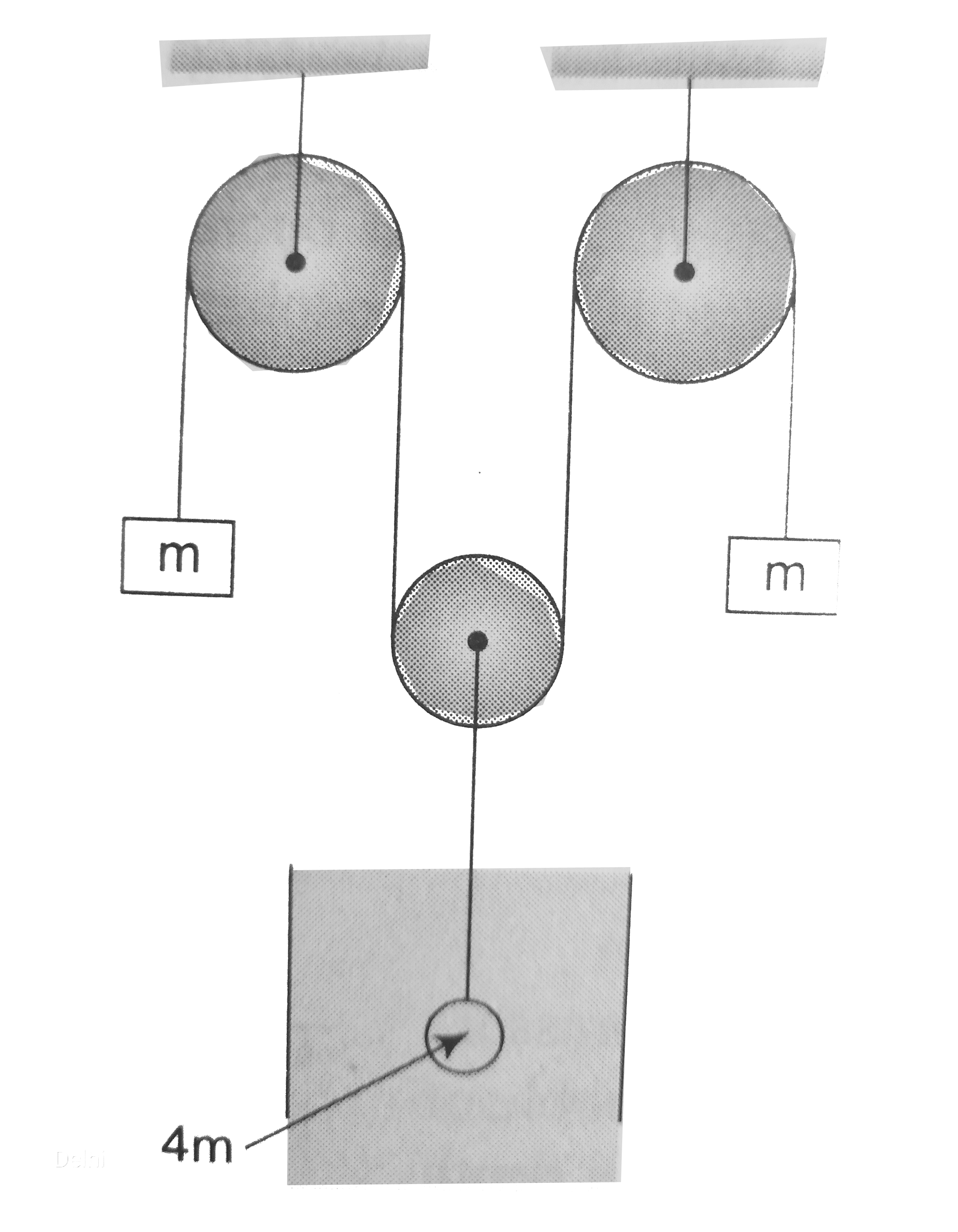
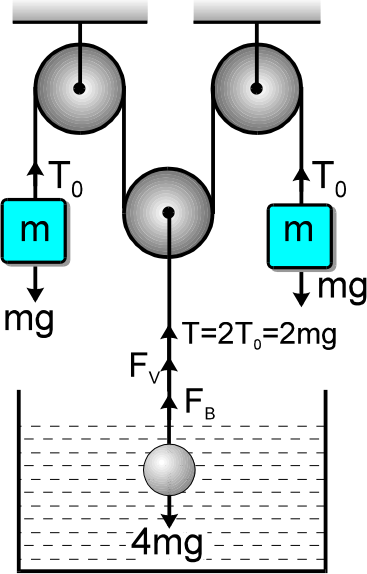
A spherical ball of mass 4m, density σ and radius r is attached to a pulley-mass system as shown in figure. The ball is released in a liquid of coefficient of viscosity η and density ρ(<σ2). If the length of the liquid column is sufficiently long, the terminal velocity attained by the ball is given by (assume all pulleys to be massless and string as massless and inextensible):
g(r2(2σ−ρ)g)9η
g(r2(σ−2ρ)g)3η
g(r2(σ−4ρ)g)3η
g(r2(σ−2ρ)g)9η
From the free body diagrame of the sphere :
Fv=4mg−2mg−FB
⇒Fv=2mg−FB
⇒6πηrV=43πr3(σ2−ρ)g
(since 4π=43πr3×σ)
⇒V=19r2(σ−2ρ)gη
Topper's Solved these Questions
Similar Questions
A small steel ball of radius r is allowed to fall under gravity through a column of a viscous liquid of coefficient of viscosity η. After some time the velocity of the ball attains a constant value known as terminal velocity υT. The terminal velocity depends on (i) the mass of the ball m (ii) η, (iii) r and (iv) acceleration due to gravity g . Which of the following relations is dimensionally correct?
View SolutionA ball of mass m and radius r rolls inside a hemispherical shell of radius R. It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is.
 .
.
View SolutionA small steel ball of radius r is allowed to fall under gravity through a column of a viscous liquid of coefficient of viscosity η. After some time the velocity of the ball attains a constant value known as terminal velocity υT. The terminal velocity depends on (i) the mass of the ball m (ii) η, (iii) r and (iv) acceleration due to gravity g . Which of the following relations is dimensionally correct?
View SolutionA small steel ball of radius r is allowed to fall under gravity through a column of a viscous liquid of coefficient of viscosity η. After some time the velocity of the ball attains a constant value known as terminal velocity υT. The terminal velocity depends on (i) the mass of the ball m (ii) η, (iii) r and (iv) acceleration due to gravity g . Which of the following relations is dimensionally correct?
View SolutionThree masses m1,m2andm3 are attached to a string -pulley system as shown . All the three masses are held at rest and then released If m3 remains at rest , then

View SolutionTwo copper balls of radius r and 2r are released at rest in a long tube filled with liquid of uniform viscosity. After some time when both the spheres acquire critical velocity (terminal velocity) then ratio of viscous force on the balls is :
View SolutionA solid ball of density ρ1 and radius r falls vertically through a liquid of density ρ2. Assume that the viscous force acting on the ball is F=krv, where k is a constant and v its velocity. What is the terminal velocity of the ball ?
View SolutionIn the given figure, Find mass of the block A, if it remains at rest, when the system is released from rest. Pulleys and strings are massless. [g=10m/s2]

View SolutionA spherical ball of density ρ and radius0.003m is dropped into a tube containing a viscous fluid up to the 0 cm mark as shown in the figure. Viscosity of the fluid =1.26N−s/m2 and its density ρL=ρ2=1260kg/m3. Assume that the ball reaches a terminal speed at 10cm mark. The time taken by the ball to travel the distance between the 10cm and 20cm mark is (g=10m/s2)

View SolutionAn iron sphere of diameter 10 mm falls through a column of oil of density 940kg/m3 . The density of iron is. 7.8×103kg/m3. The coefficient of viscosity of oll is4.48Ns/m2. Caleulate the terminal velocity attained by the ball.
View Solution
