In a spring block system on a horizontal smooth surface. K = spring constant, A = amplitude, m = mass of the block. In column I some changes are given and column II respective effect is written. Then select the correct answer using the codes given below the columns. :
Column-IColumn-II(P) if mass of the block is doubled (keeping K,A unchanged)(1)time period increases(Q) if the amplitude of oscillation is doubled (keeping m,A unchanged)(2)time period decreases(R) If force constant is doubled (keeping m, A unchanged )(3)energy of oscillation increases(S) if another spring of same force constant is attached parallel to the previous one (keeping m, A unchanged)(4)energy of oscillation remains constant
PQRS(A)1323
PQRS(B)2134
PQRS(C)3412
PQRS(D)4231
To solve the problem, we will analyze each statement in Column I and determine its corresponding effect in Column II based on the principles of oscillatory motion in a spring-block system.
Step 1: Analyze Statement (P)
Statement (P): If the mass of the block is doubled (keeping K, A unchanged).
The time period T of a mass-spring system is given by the formula:
T=2π√mK
If the mass m is doubled, the new mass becomes 2m. Thus, the new time period T′ becomes:
T′=2π√2mK=2π√2√mK=√2T
Since √2>1, the time period increases.
Effect: (1) "time period increases".
Step 2: Analyze Statement (Q)
Statement (Q): If the amplitude of oscillation is doubled (keeping m, K unchanged).
The time period T of a mass-spring system does not depend on the amplitude A. Therefore, doubling the amplitude does not affect the time period.
Effect: (4) "energy of oscillation remains constant".
Step 3: Analyze Statement (R)
Statement (R): If the force constant is doubled (keeping m, A unchanged).
The time period T is inversely proportional to the square root of the spring constant K:
T=2π√mK
If K is doubled, the new time period T′ becomes:
T′=2π√m2K=T√2
Since 1√2<1, the time period decreases.
Effect: (2) "time period decreases".
Step 4: Analyze Statement (S)
Statement (S): If another spring of the same force constant is attached parallel to the previous one (keeping m, A unchanged).
When two springs are attached in parallel, the effective spring constant K′ becomes:
K′=K+K=2K
Using the time period formula:
T′=2π√m2K=T√2
The time period decreases, and the energy of the oscillation, given by E=12KA2, increases because K is now 2K.
Effect: (3) "energy of oscillation increases".
Final Summary of Effects
- (P) → (1) "time period increases"
- (Q) → (4) "energy of oscillation remains constant"
- (R) → (2) "time period decreases"
- (S) → (3) "energy of oscillation increases"
Final Answer
The correct matches are:
- P → 1
- Q → 4
- R → 2
- S → 3
Statement (P): If the mass of the block is doubled (keeping K, A unchanged).
T=2π√mK
If the mass m is doubled, the new mass becomes 2m. Thus, the new time period T′ becomes:
T′=2π√2mK=2π√2√mK=√2T
Since √2>1, the time period increases.
Statement (Q): If the amplitude of oscillation is doubled (keeping m, K unchanged).
Statement (R): If the force constant is doubled (keeping m, A unchanged).
T=2π√mK
If K is doubled, the new time period T′ becomes:
T′=2π√m2K=T√2
Since 1√2<1, the time period decreases.
Statement (S): If another spring of the same force constant is attached parallel to the previous one (keeping m, A unchanged).
K′=K+K=2K
Using the time period formula:
T′=2π√m2K=T√2
The time period decreases, and the energy of the oscillation, given by E=12KA2, increases because K is now 2K.
- (P) → (1) "time period increases"
- (Q) → (4) "energy of oscillation remains constant"
- (R) → (2) "time period decreases"
- (S) → (3) "energy of oscillation increases"
The correct matches are:
- P → 1
- Q → 4
- R → 2
- S → 3
Topper's Solved these Questions
Similar Questions
Match Column-I with Column-II and select the correct answer using the code given below the Columns

View SolutionMatch Column-I with Column-I and select the correct answer using the codes given below :

View SolutionMatch Column I with Column II and select the correct answer using the codes given.
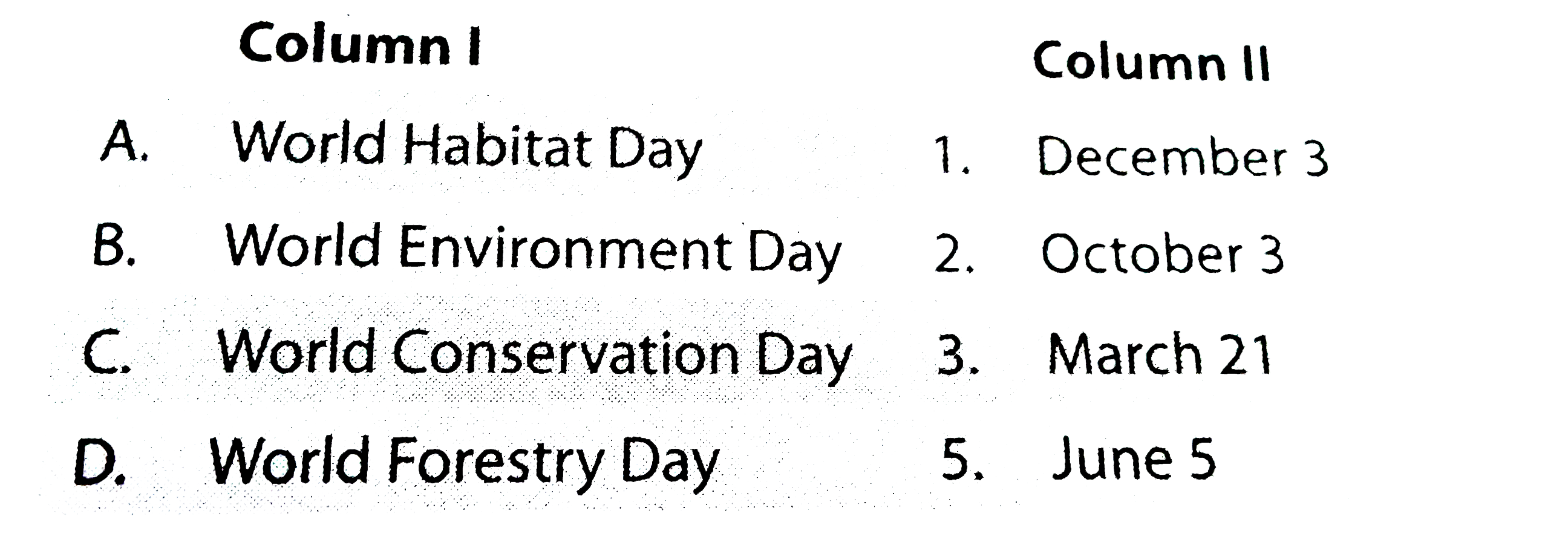
View SolutionMatch column I with column II and select the correct option using the codes given below:

View SolutionMatch Column-I with Column-II and select the correct option using the codes given below
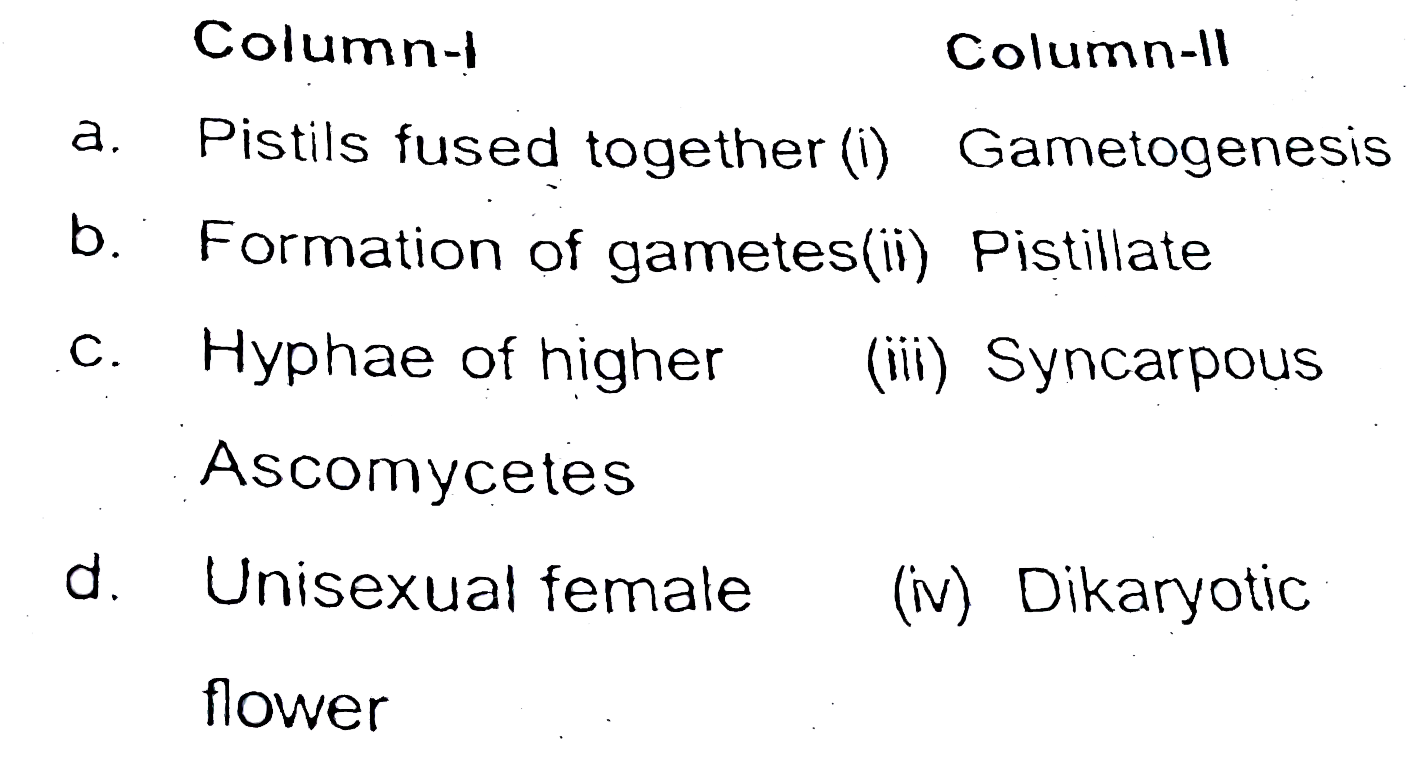
View SolutionMatch Column-I with Column-II and select the correct answer from the codes given below. :-
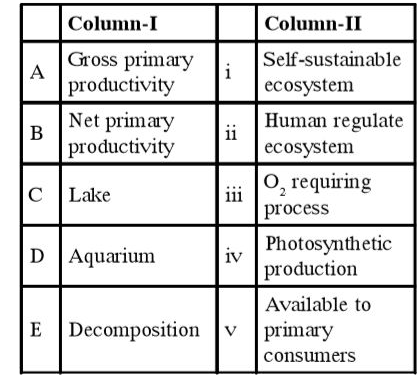
View SolutionMatch Column-I with Column-II and select the correct option using the codes given below.
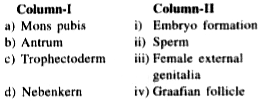
View SolutionMatch Column-I with Column -II and select the correct option using the codes given below
View SolutionMath column I with Column II and select the correct options from the choices given below the columns.

View SolutionMatch column-I with column-II and select the correct answer from the codes gives below.
View Solution

