In Young's double slit experiment, the distance between two slits is made three times then the fringe width will becomes

A

$\begin{matrix} P & Q & R & S (A) & 1 & 2 & 4 & 3 \end{matrix}$

B

$\begin{matrix} P & Q & R & S (B) & 2 & 1 & 3 & 4 \end{matrix}$

C

$\begin{matrix} P & Q & R & S (C) & 4 & 1 & 2 & 3 \end{matrix}$

D

$\begin{matrix} P & Q & R & S (D) & 4 & 2 & 3 & 1 \end{matrix}$

Video Solution

Text Solution

Verified by Experts

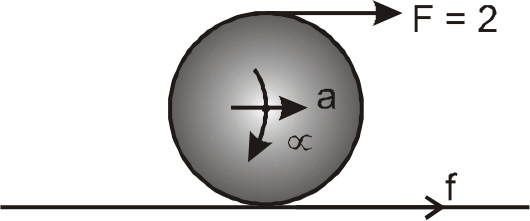
F+f=ma
FR-fR= $\frac{2}{5} m R^{2} α$
$a = R α$
$f = \frac{6}{7} N$
$f_{L} = 0.5 N \Rightarrow$ friction is kinetic
$(B) (# # R E S_{D} P P_{P} H Y_{06}_E 01_{043}_S 02 . p n g width= 80 % > < b r > 4 - f = m a < b r >$ 4xx1/2+fxx1=2a $< b r > f = 2 N < b r >$ f_(L)=3N $< b r > (C) < i m g a \leq ocr_image l o a d \in g = lazy s r c = https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_DPP_PHY_06_E01_044_S03.png w h = 80% mx-auto s t y \leq = background:white; > < b r >$ a=(g sin theta)/(1+l/(mR^(2)))=(10xx1/2)/(1+1/2)=10/3 m//s^(2) $< b r >$ mg sin theta-f =ma $< b r >$ f=(mg)/2-ma=10-20/3 =10/3 N $< b r >$ f_(L)=u_(s)N=2/5xx2xx10xx(sqrt(3))/2=4sqrt(3) $N s t a t i c < b r >$ (D) (##RES_DPP_PHY_06_E01_043_S04.png" width="80%">
$f_{L} = 5 N$
f=10/3 N static
$F - f = m a \Rightarrow 4 - f = 1 a$
$f \times 1 - 4 \times \frac{1}{2} = 2 \times \frac{a}{R} \Rightarrow f - 2 = 2 a, a = 2 / 3 m / s^{2}$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

In a double slit experiment, the distance between slits in increased ten times whereas their distance from screen is halved then the fringe width is
Abecomes $\frac{1}{20}$
Bbecomes $\frac{1}{90}$
Cit remains same
Dbecomes $\frac{1}{10}$

RESONANCE ENGLISH-REVISION DPP-All Questions

Home
Ask Doubt
Profile