A simple pendulum of length l swimings from a small angle . Its swinging is constrained by the smooth inclined planes OP and PC. Assuming elastic collision of the bob with the plane PC, find
angular amplitude for the motion of the bob in the left hand side of its mean possition.
.

a. Let us assume that the bob swings a maximum a maximum angle in the left hand side of the mean position in the absence of the position PC of the wall.
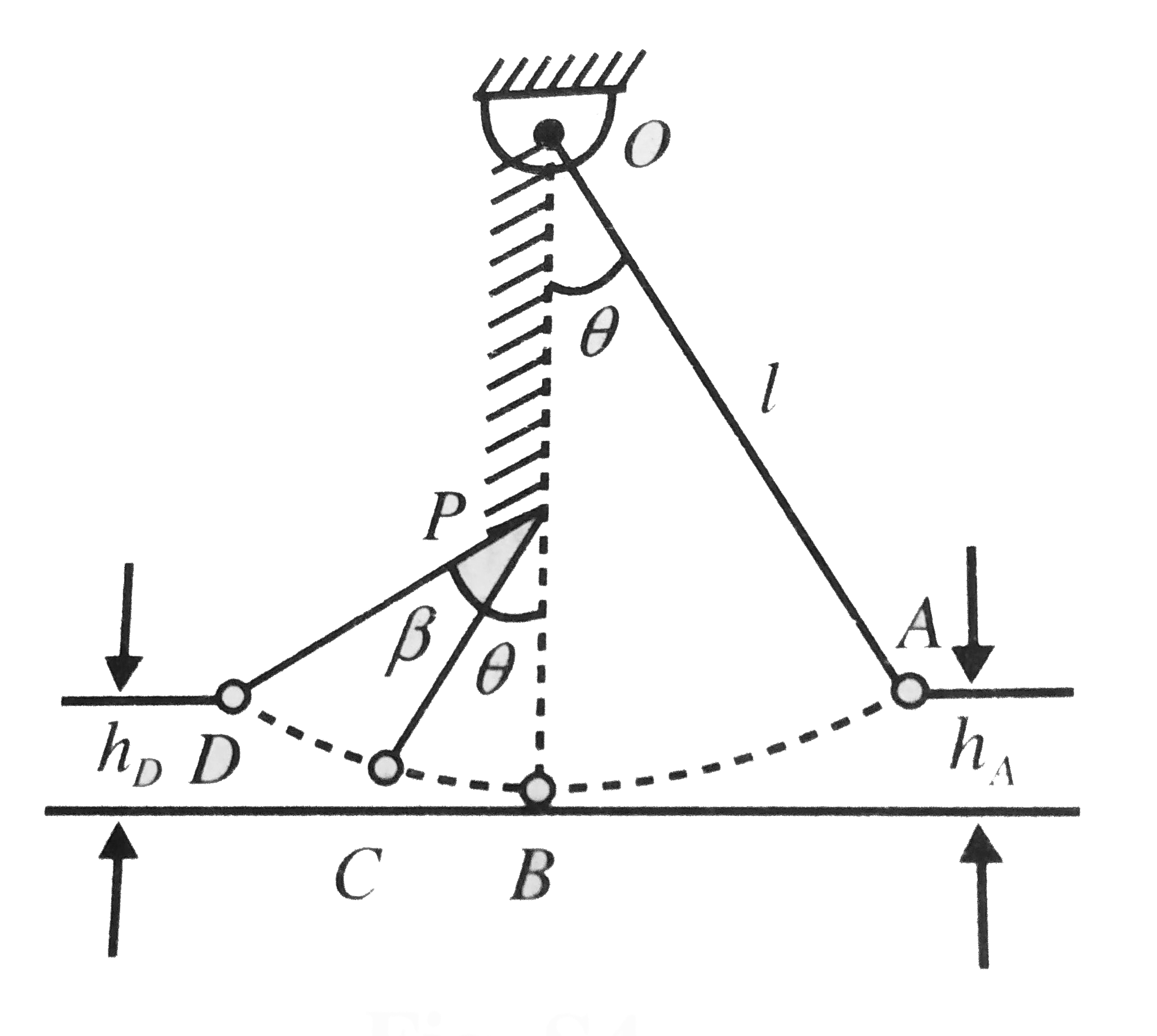
Conserving energy at A and D, we have
where
and
because the bob compes to rest at the exterme positions.
Then, we have
Substituting
and we have
Substituting , we have
b. Since the bob from A to B
where
Then
The time of miotion from B to C can be found by subsituting
and
in the equation .
where
for the swinging position of the string from B to C. This gives
Then, we have
Finally, substituting in the expression of time . , we have
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective
Explore 21 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single Correct
Explore 107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Exercise 4.1
Explore 23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
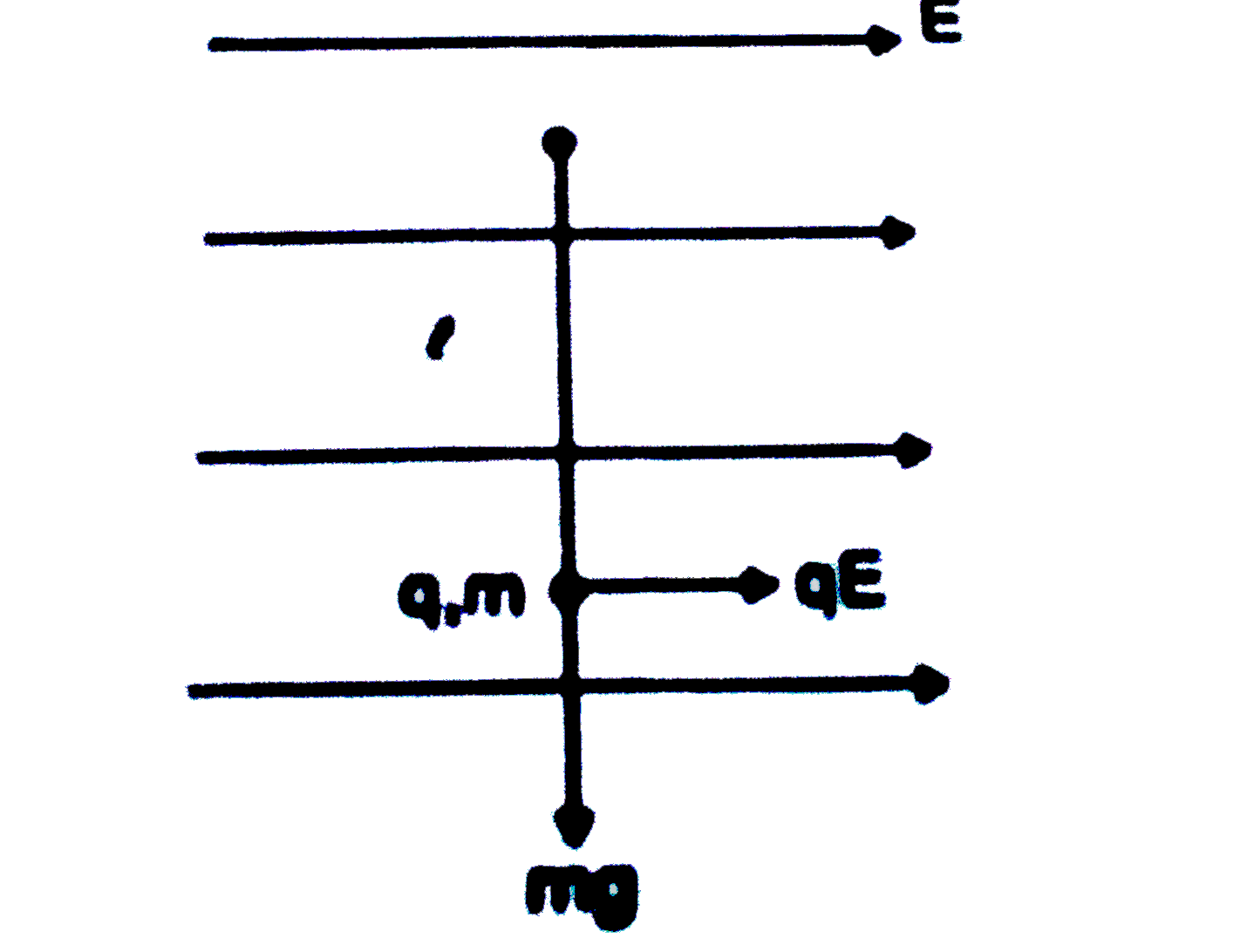
A simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.
View SolutionA simple pendilum with bob of mass m and length l is held in position at an angle θ with t he verticle. Find its speed when it passes the lowest position.
View SolutionThe bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
View SolutionA simple pendulum of length l and mass m free to oscillate in vertical plane. A nail is located at a distance d=l−a vertically below the point of suspension of a simple pendulum. The pendulum bob is released from the position where the string makes an angle of 90∘ from vertical. Discuss the motion of the bob if (a) l=2a and (b) l=2.5a.
View SolutionA simple pendulum is suspended from the ceiling of trolley which is sliding down on a inclined plane of inclination θ Find the angle made by the string with normal to the trolley a) when trolley slides down with uniform velocity b) when the plane is smooth.
View SolutionA light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.
View SolutionA wagon of mass M can move without friction along horizontal rails. A simple pendulum consisting of a sphere of mass m is suspended from the ceiling of the wagon by a string of length l. At the initial moment the wagon and the pendulum are at rest and the string is deflected through an angle α from the vertical. Find the velocity of the wagon when the pendulum passes through its mean position.
View SolutionA simple pendulum with a bob of mass m and a conducting wire of length L, swings under gravity with an angular amplitude 2θ. If the horizontal component of the earth's magnetic field perpendicular to the plane of motion of the pendulum is B, then the maximum emf induced across the pendulum is
View SolutionA simple pendulum of length L and mass (bob) M is oscillating in a plane about a vertical line between angular limit −ϕ and +ϕ. For an angular displacement θ(|θ|<ϕ), the tension in the string and the velocity of the bob are T and V respectively. The following relations hold good under the above conditions:
View Solution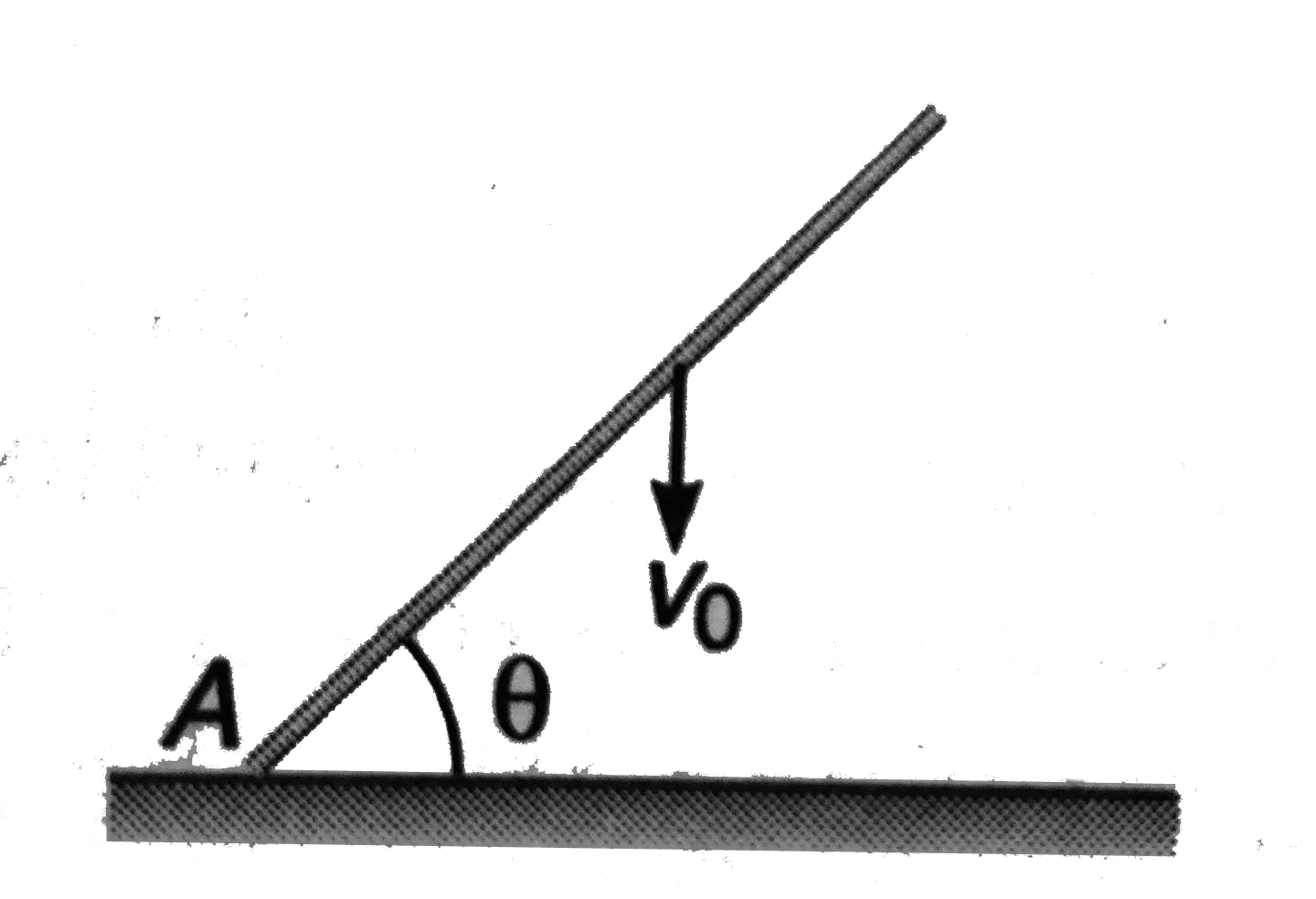
A rod of length l forming an angle θ with the horizontal strikes a frictionless floor at A with its centre of mass velocity v0 and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.
View Solution