A rigid rod of mass m with a ball of mass M attached to the free end is restrained to oscillate in a vertical plane as shown in the figure. Find the natural frequency of oscillation.

The correct Answer is:12π√3k27M+7m
At equlibrium position deformation of the spring is x0
kx0=14=Mg(34l)+mg(14)
When the rod is further rotated through an angle θ from equlibrium position, the restoring tarque.
τ=−[k(x+x0)14cosθ−Mg(34)Lcosθ]−mg(L4)cosθ
=−[k(x+x0)14−Mg(34)L−mg(L4)]cosθ
For small θ,cosθ≈1
τ=−kl4x ⇒lα=−kl24θ
l=m(34L)2+mL212+m(L4)2
f=12π√3k27M+7m
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
From the given figure find the frequency of oscillation of the mass m

View SolutionA disc of mass M = 4 kg, radius R = 1 m is attached with two blocks A and B of masses 1 kg and 2 kg respectively on rim and is resting on a horizontal surface as shown in the figure. Find angular frequency of small oscillation of arrangement:
View Solution
Knowledge Check
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
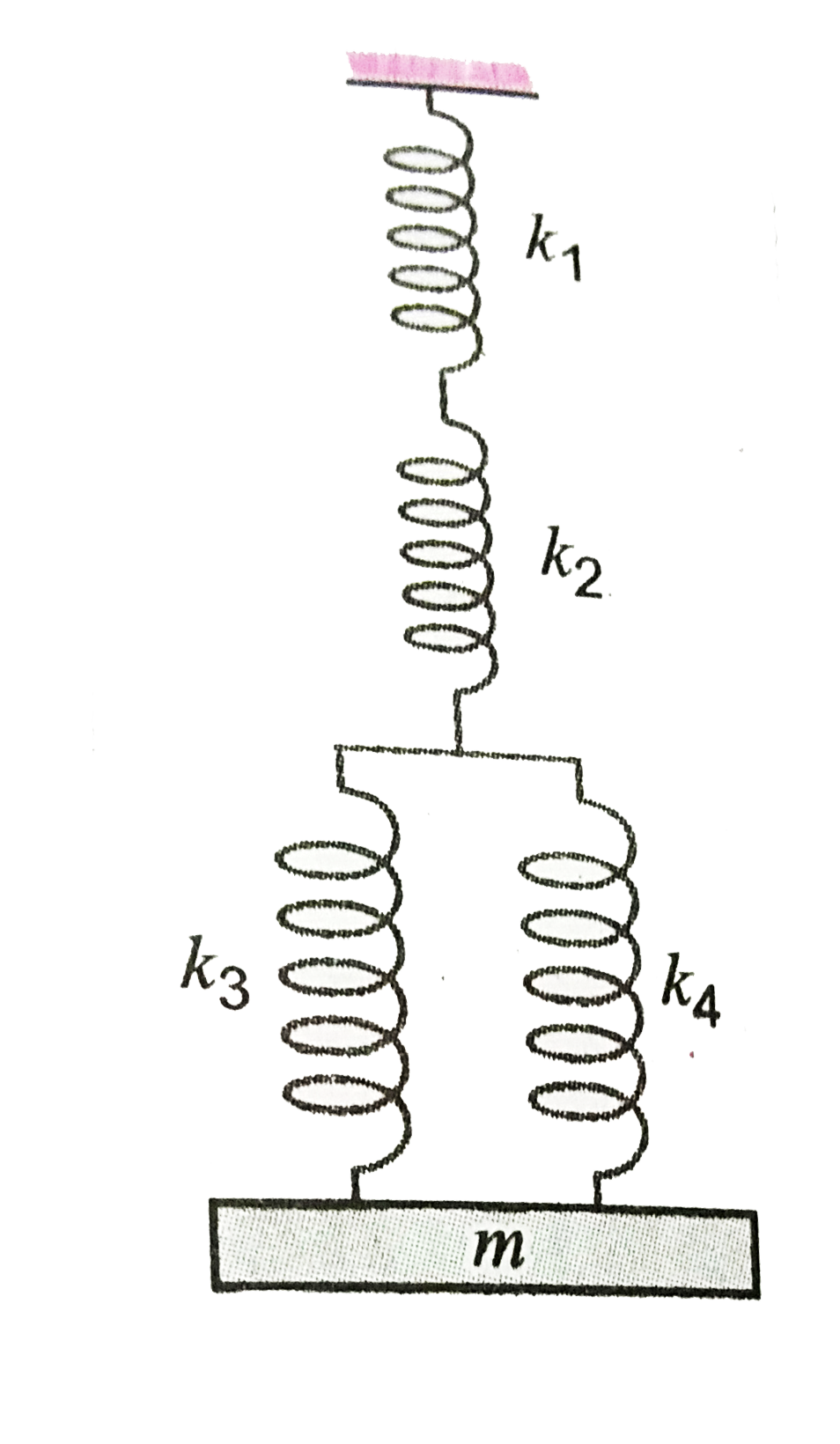 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
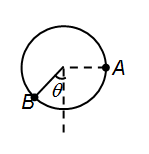
An L-shaped bar of mass M is pivoted at one of its end so that it can freely rotate in a vertical plane, as shown in the figure
a. Find the value of θ0 at equilibrum
b. If it is slighly displacement from its equilibrum position, find the frequency of oscillation.

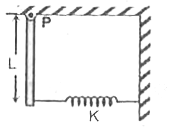
View SolutionA straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
View Solution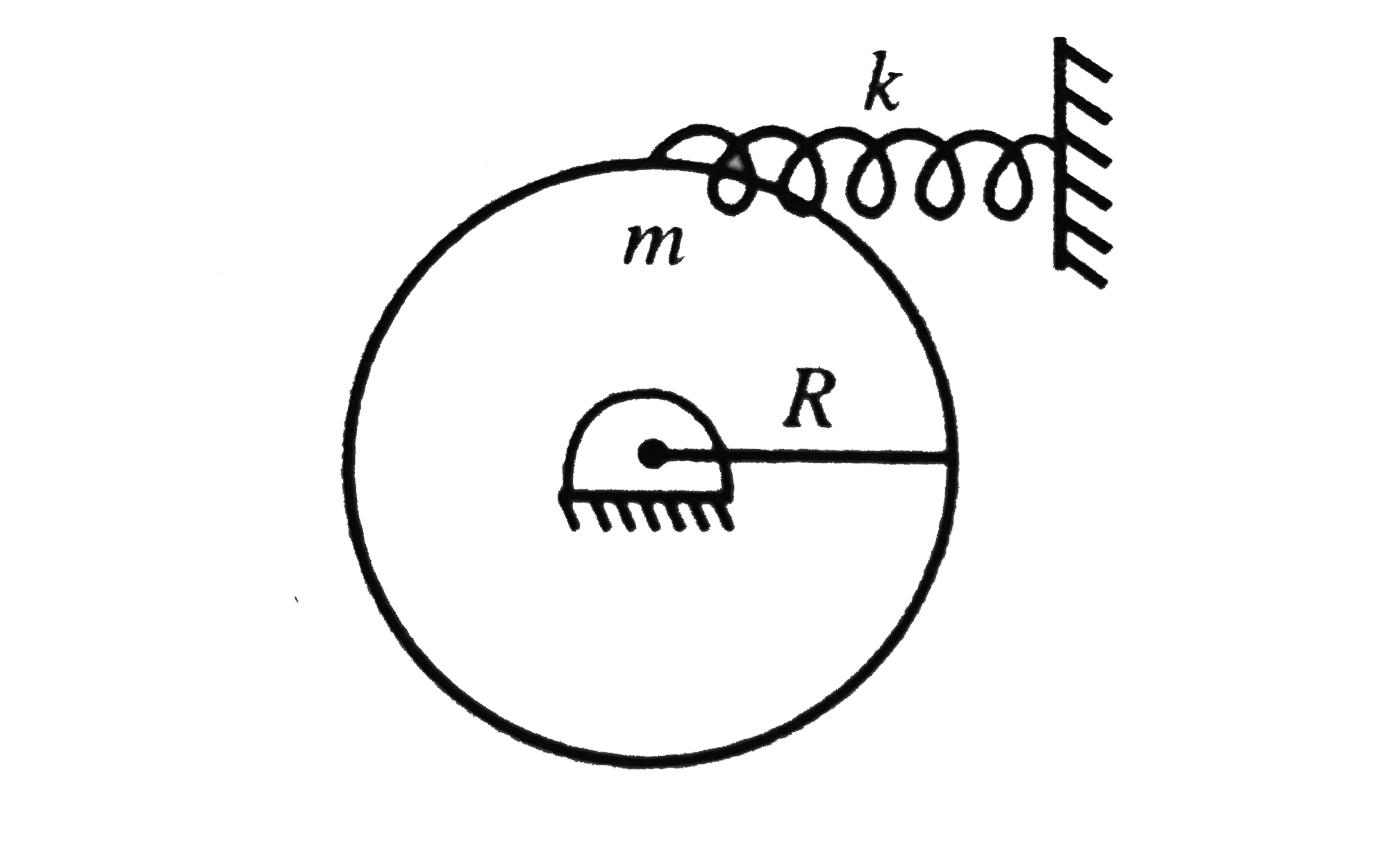
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View Solution
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is
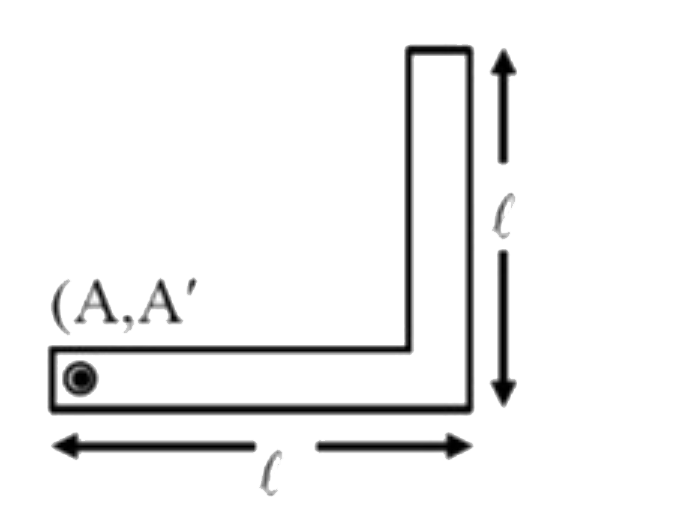
View SolutionA block of mass m connected with a smooth prismatic wedge of mass M is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

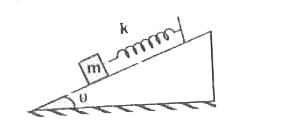
View SolutionA block of mass m can slide along a frictionless inclined plane, is attached to a ideal spring of spring constant as shown in the figure. Find the period of its oscillation. (Frame of reference attached to the wedge is at rest)
View Solution
