A stepped dies of mass M and radius R is pivoted at its center C smoothly. An inextensible string connected with a light spring of stiffness k passes over the pulley. One end of the string is rigidly connected with the ground and the other end is attached to a body of mass m . If the string does not slide on the pulley, find the angularfrequency of oscillation of the syytem

The correct Answer is:√2kR2MR2+2mr2)
The net torque produced by the spring when the dise is rotated through an angle θ is
τC=(kx)R=(IC+mr2)α
where x=RθandIC=MR2
or α=kR2(MR22+mr3)θorω=√2kR2MR2+2mr2
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A block of mass m hangs by means of a string which goes over a pulley of mass m and moment of inertia l, as shown in the diagram. The string does not realtive to the pulley. Find the frequency of small oscillations.
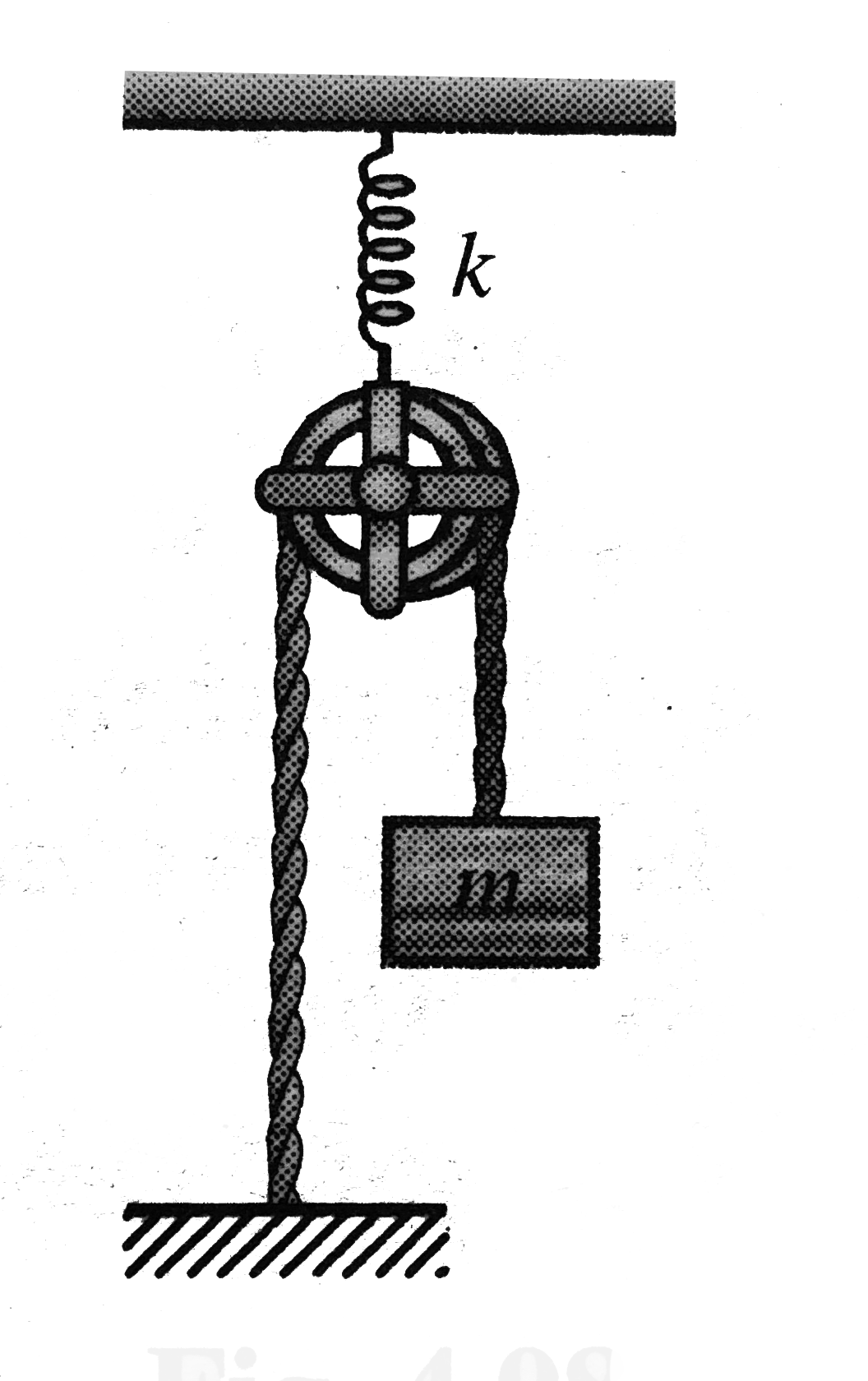
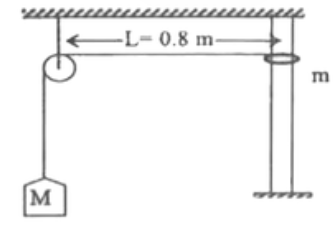
View SolutionA ring of mass m = 0.3kg can slide freely on smooth vertical rod. A light and inextensible string is connected to the ring and passes over a smooth and fixed pulley as shown in the figure. The distance of the pulley from the rod is 0.8m and the other end of the string is connected to a block of mass M = 0.5kg. The ring is held in level with pulley and then released from rest.
The distance by which the ring moves down before coming to rest for the first time is 0.75K. Find K.
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
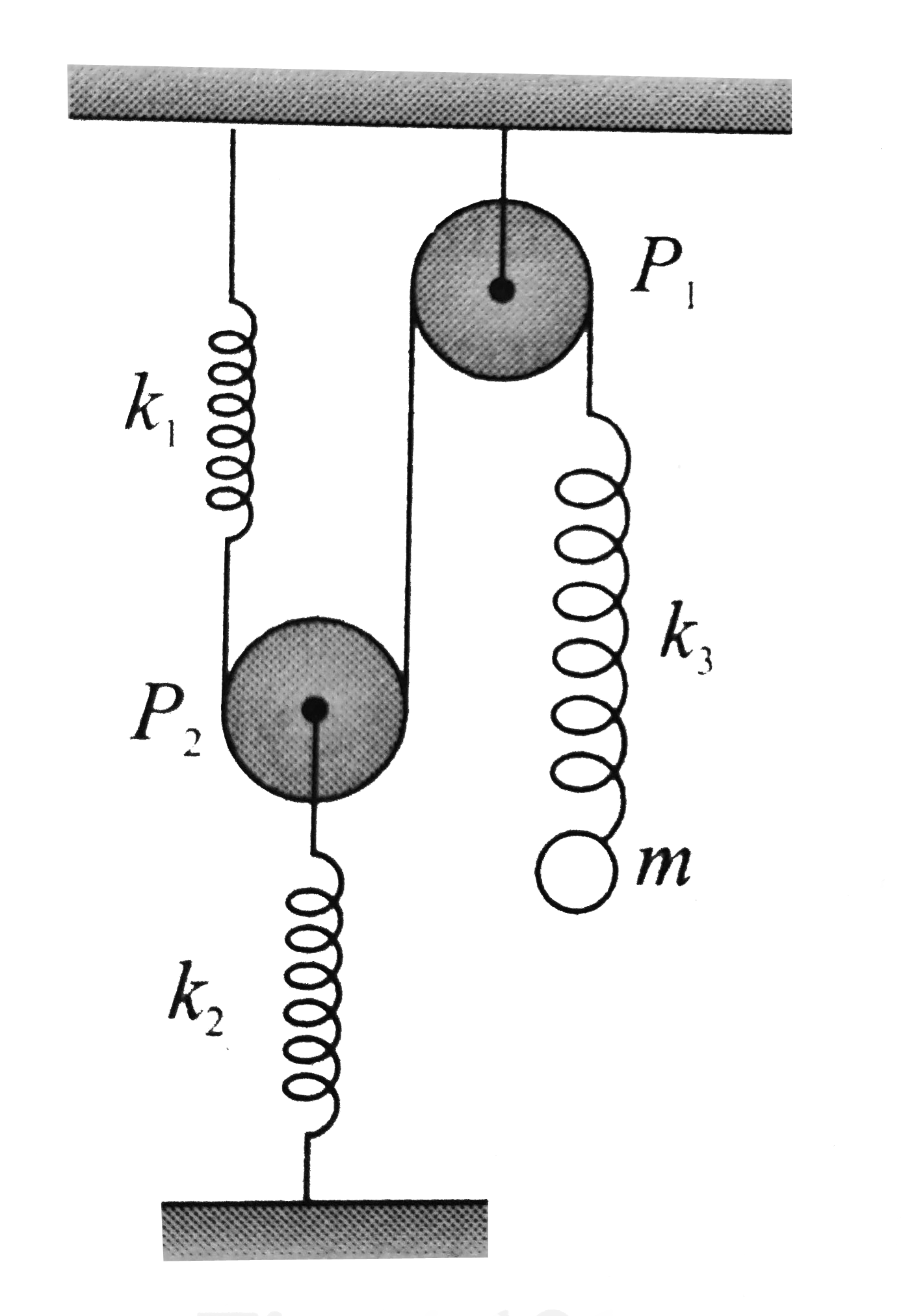
View SolutionA body of mass m hangs from a smooth fixed pulley P1 by the inextensible string fitted with the springs of stiffness k1 and k2 . The string passes over the smooth light pulley P2 which is connected with another ideal spring of stiffness k2. Find the period of oscillation of the body.
View SolutionTwo block of masses m1 and m2 are in equilibrium. The block m2 hangs from a fixed smooth pulley by an inextensible string that is fitted with a light spring of stiffness k as shown in fig. Neglecting friction and mass of the string, find the acceleration of the bodies just after the string S is cut.

View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionA stepped pulley having mass m radius of gyration k is connected with two ideal springs of stiffness k1 and k2 as shown in figure. If the pulley shown in the figure rolls without sliding, find the angular frequency of its oscillation.

View SolutionTwo block A and B of mass M & 3M are connected through a light string. One end of the string is connected to the blcok B and its other end is connected to a fixed point S as shown in fig. Now a force F is applied to block B. find the acceleration of block A & B.

View SolutionTwo unequal masses are connected by a very light string over a clamped light smooth pulley. Find the acceleration of the system and the tension in the string.
View SolutionA uniform disc of mas M and radius R is smoothly pivoted at O. A light iextensible string wrapped over the disc hangs a particle of mass m. If the system is released from rest, assuming that the string does not slide on the disc, find the angular speed of the disc as the function of time using impulse momentum equation.

View Solution
