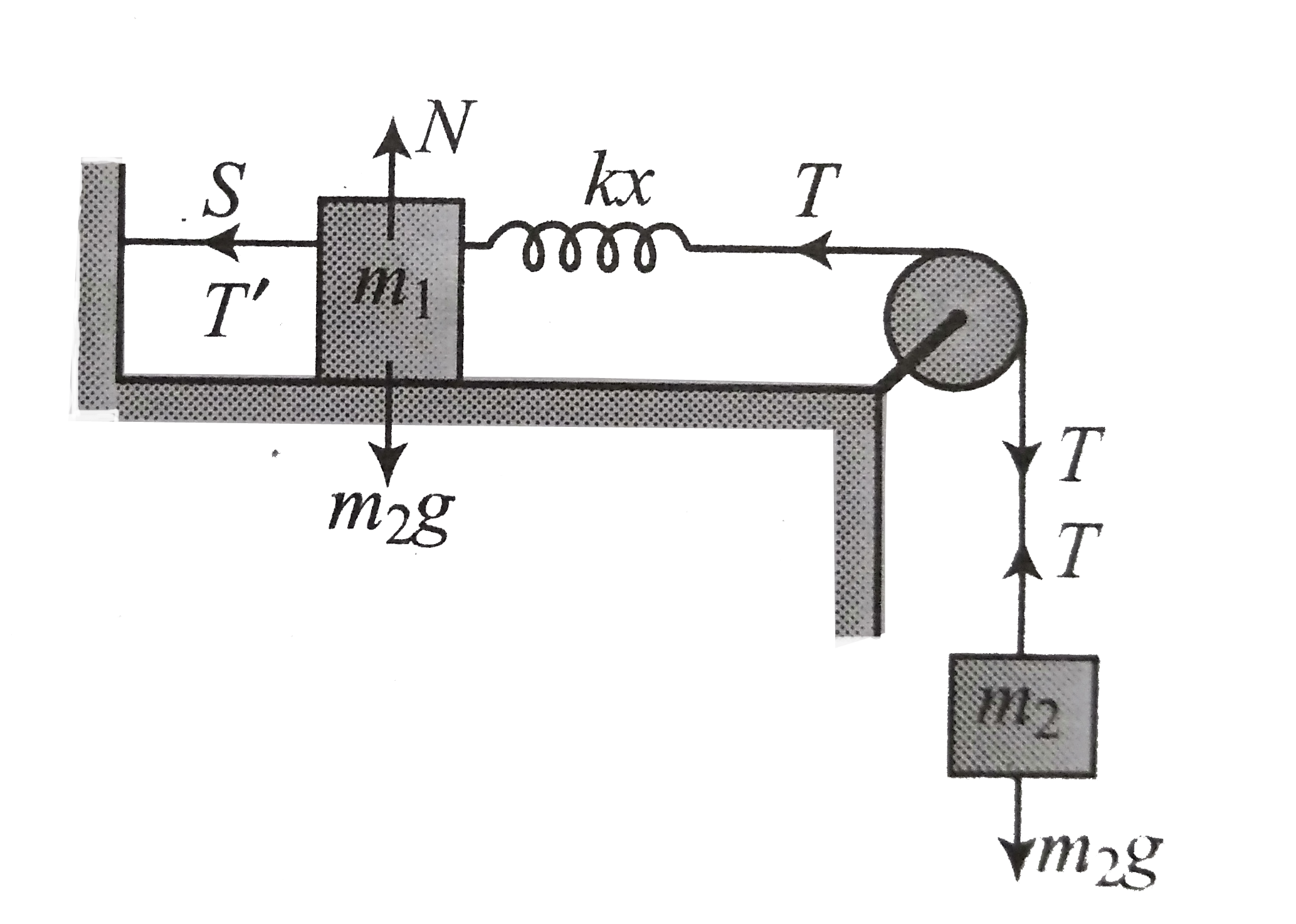
Two block of masses m1 and m2 are in equilibrium. The block m2 hangs from a fixed smooth pulley by an inextensible string that is fitted with a light spring of stiffness k as shown in fig. Neglecting friction and mass of the string, find the acceleration of the bodies just after the string S is cut.

FBD: Let the spring forces be F=kx just after cutting the spring. Hence, at that instant, the forces acting on m1 are T=kx→m1g↓andN↑, on m2 the force are m2g↓ and T↑.
Force equation: Initially, all the particles are stationary, hence, a1=a2=0. applying Newton's second law.
For m1: ΣF=T'−kx=0
For m2:ΣF=T−m2g=0
for spring: ΣF=T−kx=0
Solving eqs. (i), (ii) and (iii), we have
T'=T=kx=m2g
Just after the string S is cut, tension T' vanishes immediately but the spring cannot regain its shape and size instantanously. Therefore, the spring force remains as it is . Then, just after cutting the string, the net force acting on m1 is equal to kx, whereas the net force acting on m2 is equal to T=m2g. Hence the acceleration of m1 and m2 just after cutting the string is given by
ΣF=m1a1=kx=m2g,ΣF=m2a2=T−m2g=0
This gives a1=(m2m1)ganda2=0.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Single Correct
75 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.3
19 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
The system shown in the figure is in equilibrium at rest. The spring and string are massless Now the string is cut. Find the acceleration of the blocks just after the string is cut.
View SolutionTwo blocks A and B of same mass m attached with a light spring are suspended by a string as shown in fig. Find the acceleration of block A and B just after the string is cut.
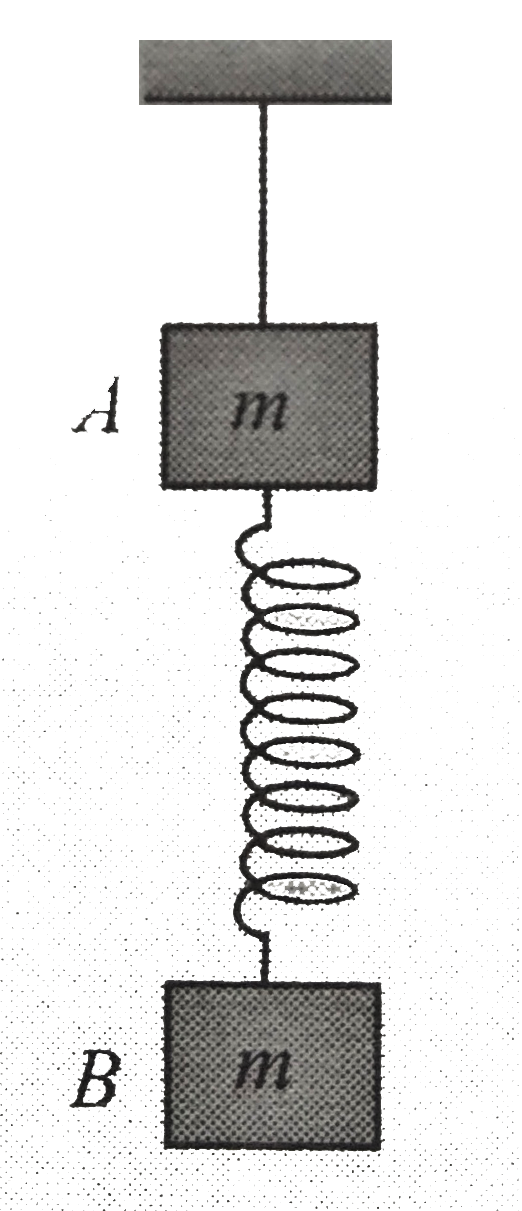
View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:

View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:

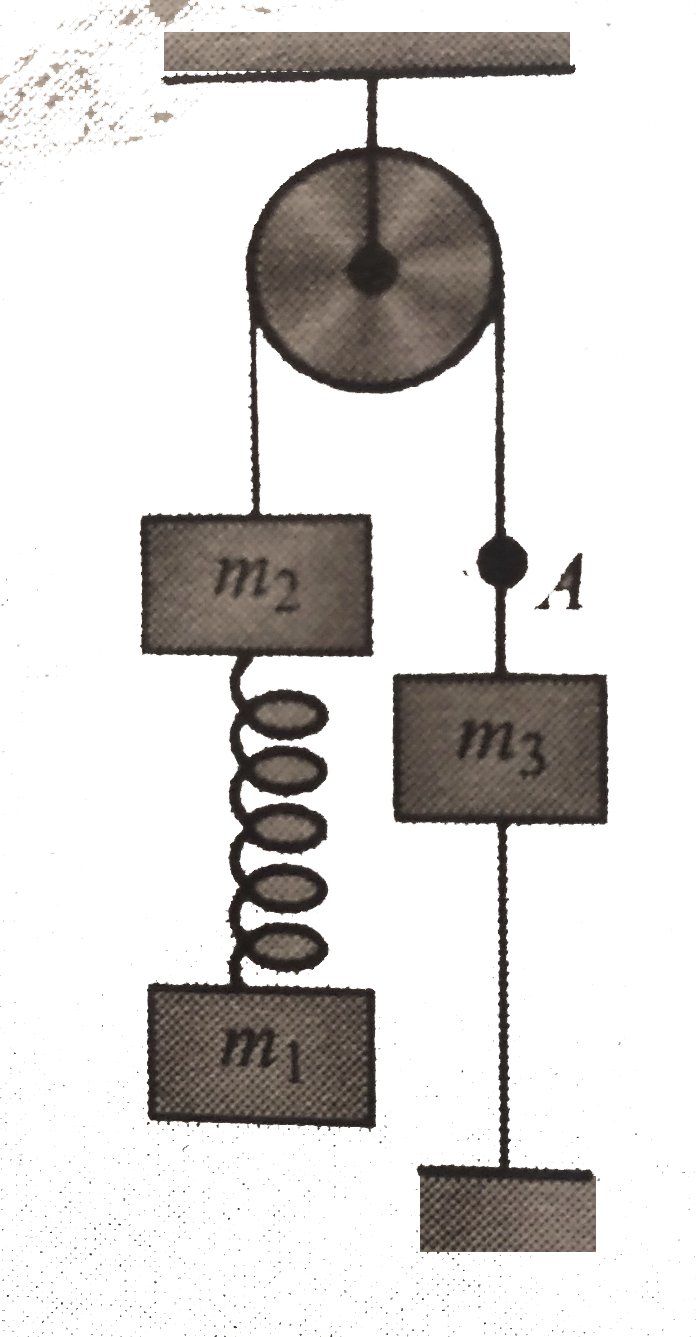
View SolutionThree blocks arranged with pullwy and spring as shown in fig. If the string connecting blocks m2 and m3 is cut at point A, find the acceleration of masses m1,m2 and m3. Just after the string is cut at point A.
View SolutionA body of mass m hangs by an inextensible string that passes over a smooth mass less pulley that is fitted with a light spring of stiffness k as shown in figure. If the body is released from rest and the spring is released, calculate the maximum elongation of the spring.
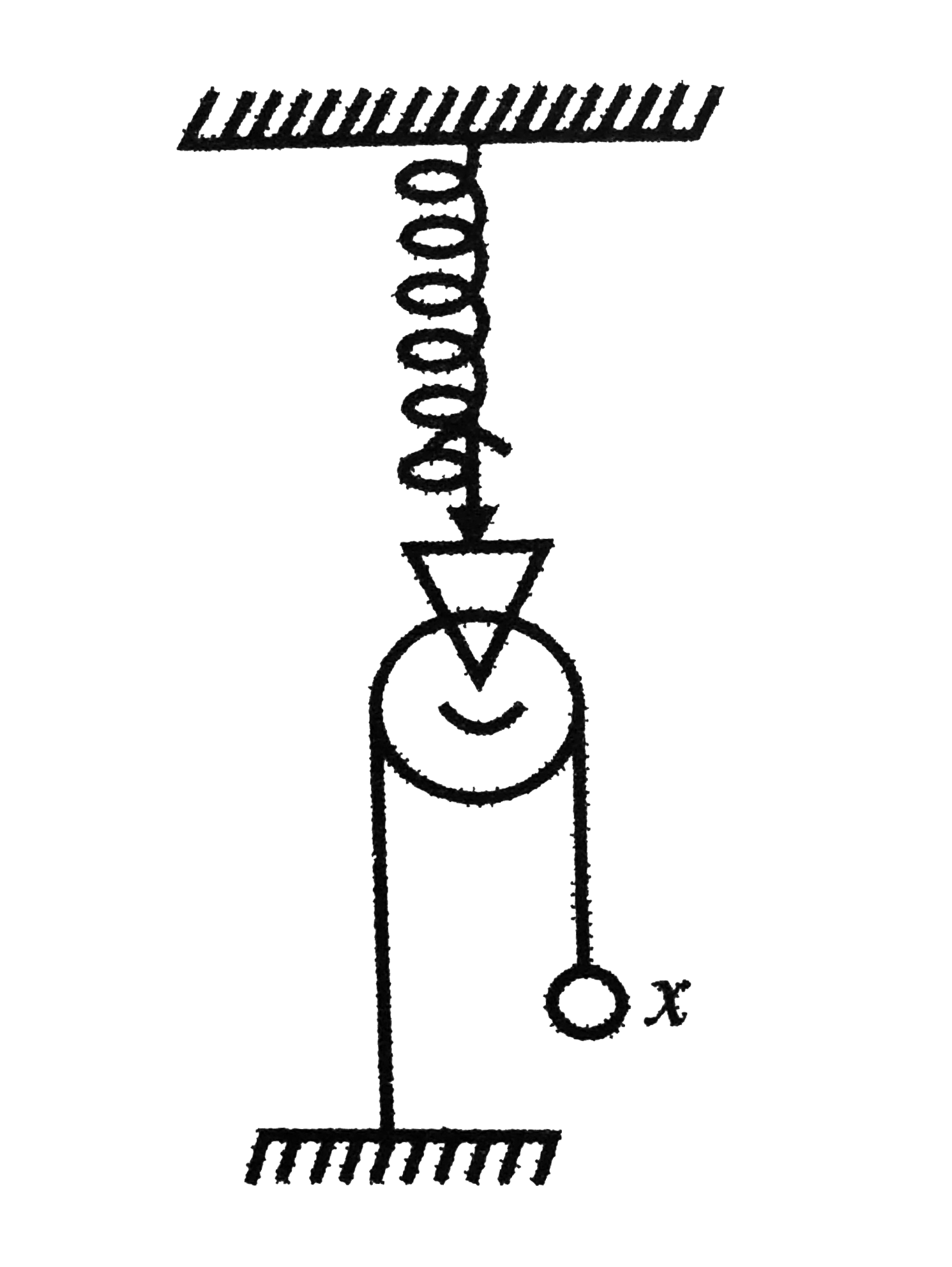
View SolutionA block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.

View SolutionTwo block of mass 4 kg and 5 kg attached a light spring are suspended by a string as shown in figure. Find acceleration of block 5 kg and 4 kg just after the string is cut.
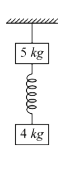
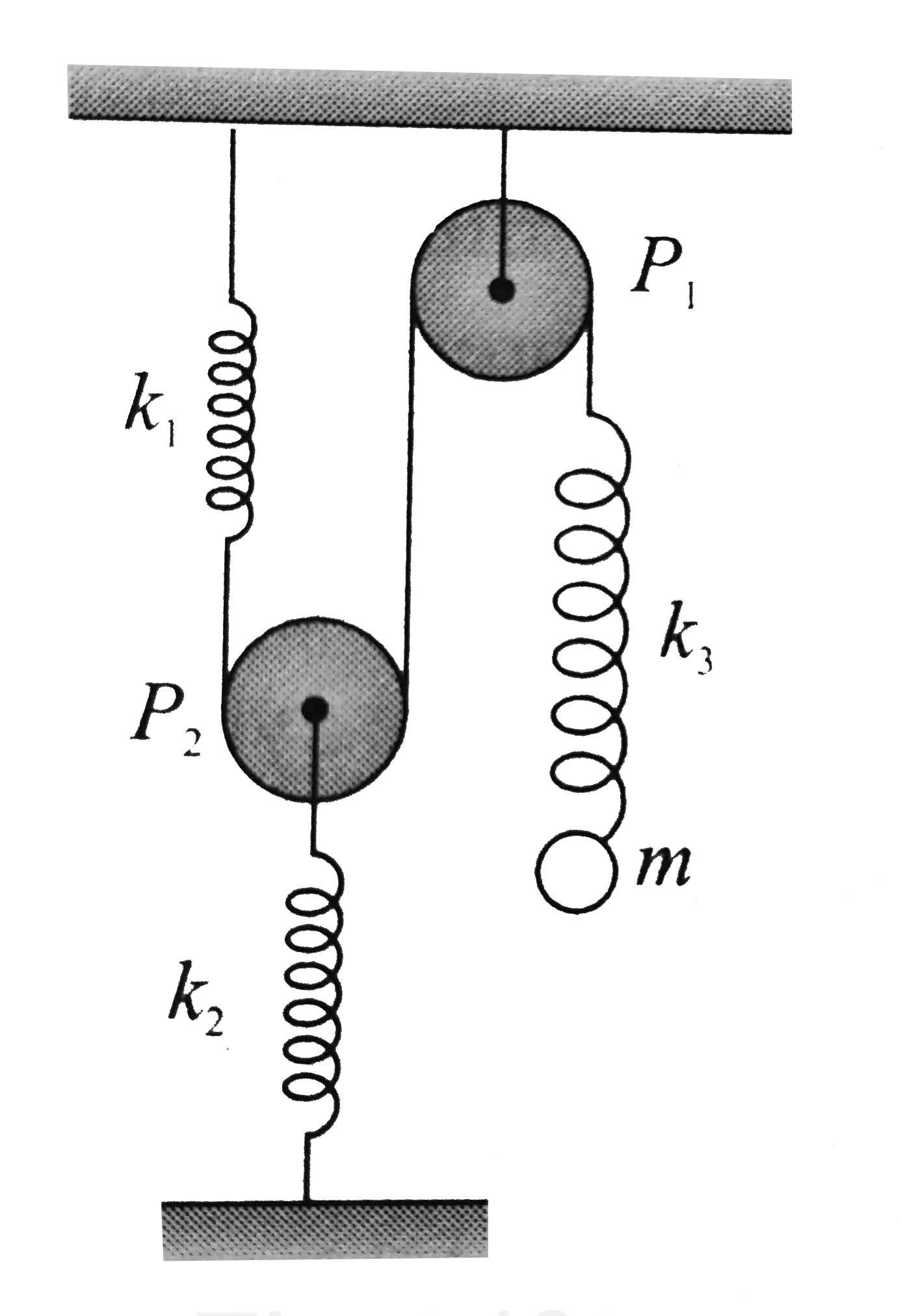
View SolutionA body of mass m hangs from a smooth fixed pulley P1 by the inextensible string fitted with the springs of stiffness k1 and k2 . The string passes over the smooth light pulley P2 which is connected with another ideal spring of stiffness k2. Find the period of oscillation of the body.
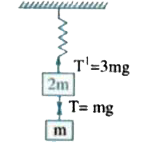
View SolutionTwo block A and B of masses 3m and m respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in figure. The magnitudes of acceleration of A and B immediately after the string is cut, are resectively
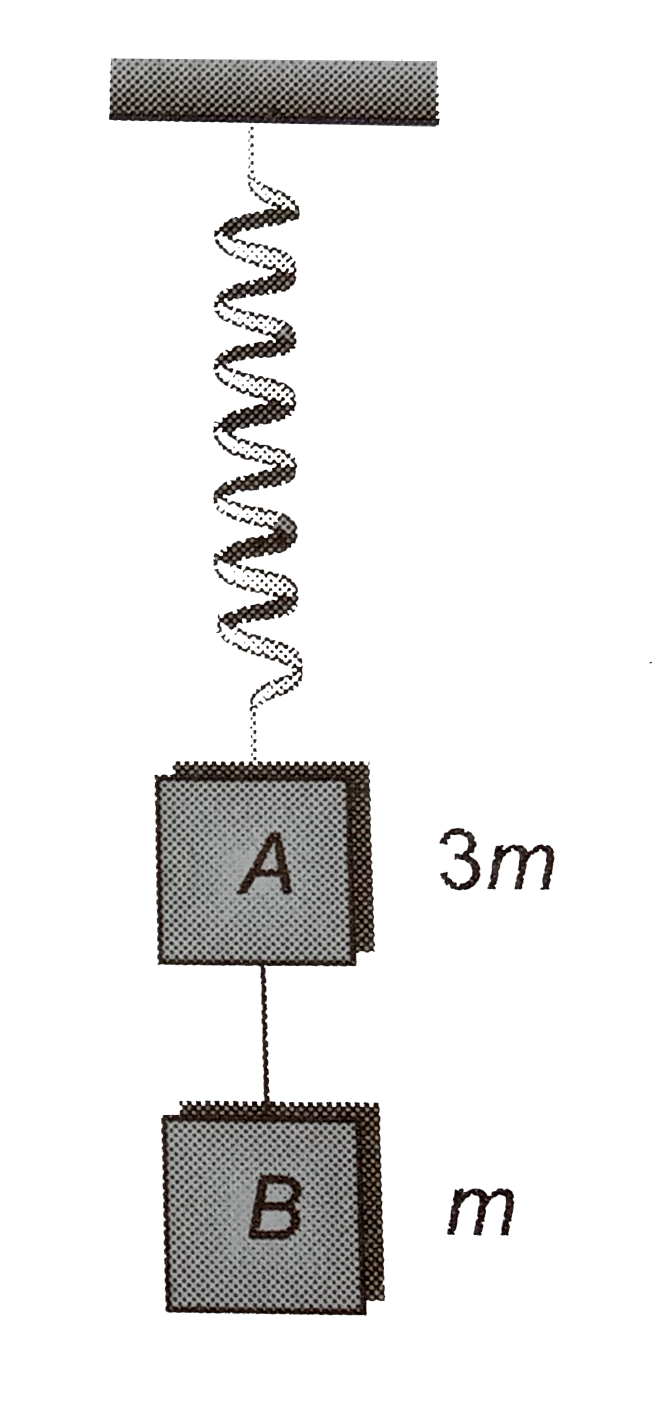
View Solution
