A material having an index of refraction of 1.30 is used as an antireflective coating on a piece of glass (n = 1.50). What should be the minimum thickness of this film in order to minimize reflection of 500 nm light?
To find the minimum thickness of an antireflective coating that minimizes reflection for light of wavelength 500 nm, we can follow these steps:
1. Understand the Problem: We have an antireflective coating with a refractive index n=1.30 applied to glass with a refractive index ng=1.50. We need to minimize the reflection of light with a wavelength λ=500 nm.
2. Identify the Condition for Minimum Reflection: For a thin film, the condition for destructive interference (which minimizes reflection) is given by the formula:
2nt=(m+12)λ
where t is the thickness of the film, n is the refractive index of the film, λ is the wavelength of light in vacuum, and m is an integer (0, 1, 2,...).
3. Set Up the Equation for Minimum Thickness: For the minimum thickness, we can set m=0:
2nt=12λ
Rearranging gives:
t=λ4n
4. Substitute Values: Now we can substitute the values into the equation. The wavelength λ=500 nm (which is 500×10−9 m) and n=1.30:
t=500×10−94×1.30
5. Calculate the Thickness:
t=500×10−95.2≈96.15×10−9 m=96.15 nm
6. Final Result: The minimum thickness of the antireflective coating is approximately 96.15 nm.
Summary:
The minimum thickness of the antireflective coating required to minimize reflection of 500 nm light is approximately 96.15 nm.
2nt=(m+12)λ
where t is the thickness of the film, n is the refractive index of the film, λ is the wavelength of light in vacuum, and m is an integer (0, 1, 2,...).
2nt=12λ
Rearranging gives:
t=λ4n
t=500×10−94×1.30
t=500×10−95.2≈96.15×10−9 m=96.15 nm
The minimum thickness of the antireflective coating required to minimize reflection of 500 nm light is approximately 96.15 nm.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.2
22 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Solved Examples
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
A film with index of refraction 1.50 coats a glass lens with index of refraction 1.80. What is the minimum thickness of the thin film that will strongly reflect light with wavelength 600 nm?
View SolutionHigh-quality camera lenses are often coated to prevent reflection. A lens has an optical index of refraction of 1.72 and a coating with an optical index os refraction 1.31. For near normal incidence, the minimum thickness of the coating to prevent reflection for wavelength of 5.3×10−7m is
View SolutionA parallel beam of light of wavelength 560 nm falls on a thin film of oil (refractive index = 1.4). What should be the minimum thickness of the film so that it strongly transmit the light ?
View SolutionBlue light of wavelength 480 nm is most strongly reflected off a thin film of oil on a glass slab when viewed near normal incidence. Assuming that the index of refraction of the oil is 1.2 and that of the glass is 1.6, what is the minimum thickness of the oil film (other then zero)?
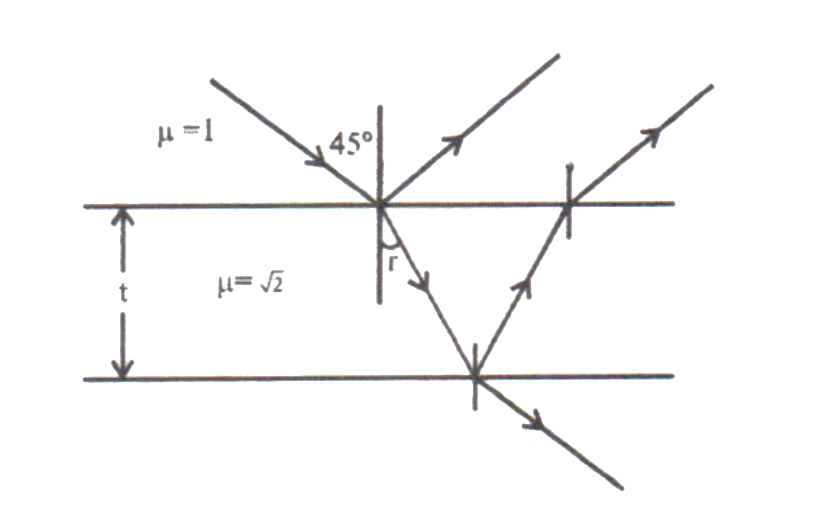
View SolutionA ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
View SolutionA thin film with index of refraction 1.33 coats a glass lens with index of refraction 1.50. Which of the following choices is the smallest film thickness that will not reflect light with wavelength 640 nm?
View SolutionA certain region of a soap bubble reflects red light of vacuum wavelength λ=650nm. What is the minimum thickness that this region of the soap bubble could be have? Take the index of reflection of the soap film to be 1.41.
View SolutionA glass lens is coated on one side with a thin film of magnesium fluoride (MgF2)to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of MgF2 is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm (λ=550nm)? Assume that the light is approxmately perpendicular to the lens surface.
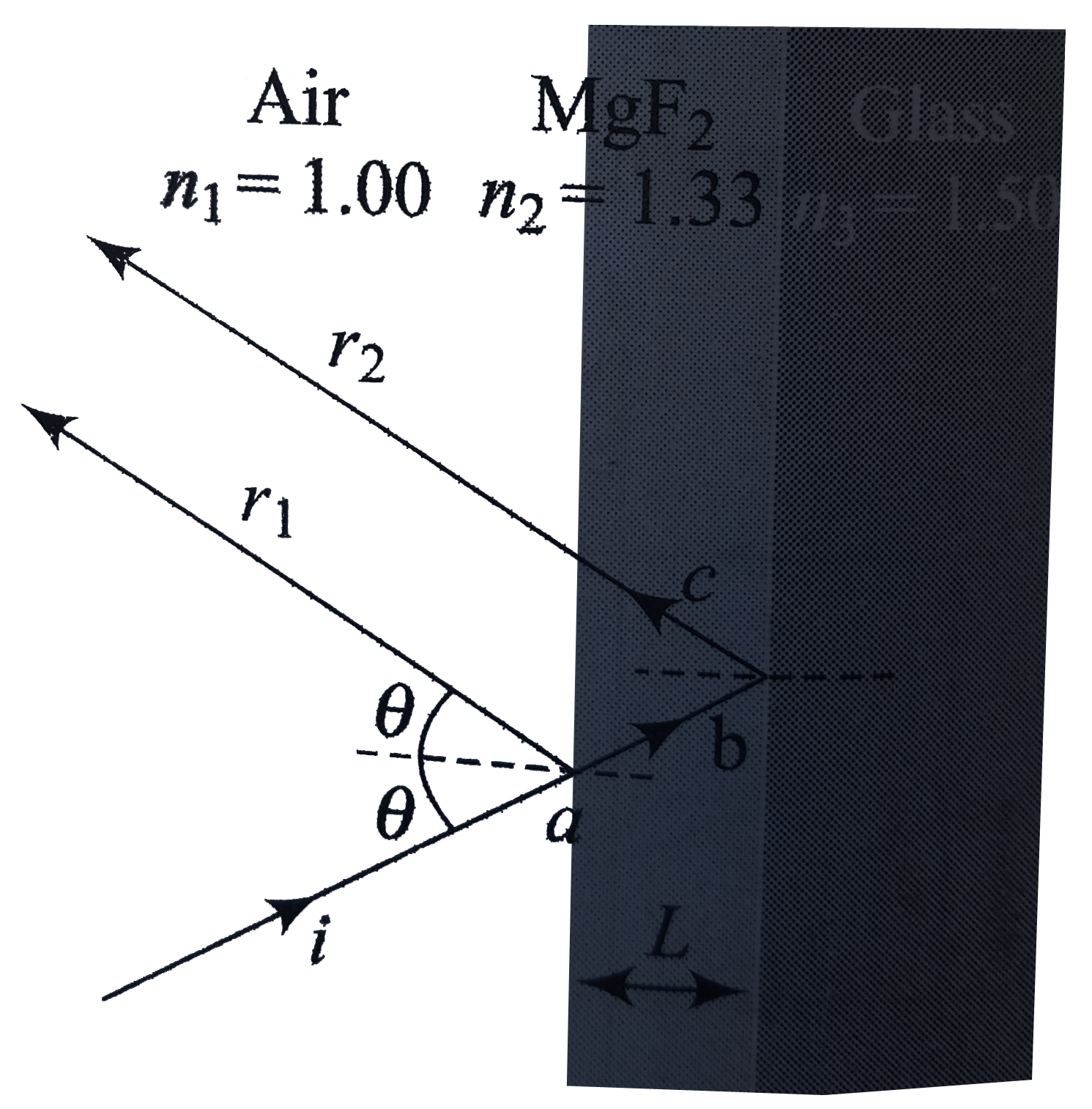
View SolutionA thin film of thickness t and index of refractive 1.33 coats a glass with index of refraction 1.50.What is the least thickness t that will strong reflect light with wavelength 600nm incident normally?
View SolutionA thin film of a specific meterial can be used to decrease the intensity of reflected light. There is destrucive inteference of wave reflected from upper and lower surface of the film. These films are called non-reflecting or anti-reflecting coatings. The process of coating the lens or surface with non-reflecting film is called blooming as shown in figure The refracting index of coating (n1) is less than that of the glass (n2).

5. magnesium fluoride (MgF2) is generally use as anti-reflection coating. If refractive index of MgF2 is 1.25, then minimum thickness of film required is (Take λ=500nm)
View Solution
