By an anodizing process, a transparent film of aluminium oxide of thickness t=250 nm and index of refraction n2=1.80 is deposited on a sheet of polished aluminium What is the color of utenslis made from this sheet with observer in white light? Assume normal incidence of the light.
To determine the color of utensils made from a sheet of polished aluminum with a transparent film of aluminum oxide, we will analyze the phase change upon reflection and calculate the wavelength of light that will be constructively interfered.
1. Identify the Given Data:
- Thickness of the aluminum oxide film, t=250 nm.
- Refractive index of aluminum oxide, n2=1.80.
- Refractive index of air (for simplicity), n1=1.00.
2. Determine the Phase Change upon Reflection:
- Light reflecting off a denser medium (from air to aluminum oxide) undergoes a phase change of π (or 180 degrees).
- Light reflecting off a less dense medium (from aluminum oxide to aluminum) does not undergo a phase change, so it remains at 0.
3. Calculate the Total Phase Difference:
- The total phase difference Δϕ can be calculated as:
Δϕ=ϕ1−ϕ2=π−0=π
4. Calculate the Path Difference:
- The path difference Δx corresponding to the phase difference of π is given by:
Δx=λ2
- Since we have a film of thickness t, the effective path difference due to the film is:
Δx=2n2t
5. Set the Path Difference Equal to the Wavelength Condition:
- Setting the two expressions for path difference equal gives:
2n2t=λ2
- Rearranging gives:
λ=4n2t
6. Substitute the Values:
- Substitute n2=1.80 and t=250 nm into the equation:
λ=4×1.80×250 nm
λ=1800 nm
7. Determine the Wavelength in Terms of Visible Light:
- Since 1800 nm is outside the visible spectrum (which ranges from approximately 400 nm to 700 nm), we need to consider the constructive interference for lower orders.
- The first visible wavelength can be calculated by considering n=1 and n=2:
- For n=1:
λ1=18001=1800 nm(not visible)
- For n=2:
λ2=18002=900 nm(not visible)
- For n=3:
λ3=18003=600 nm(visible, red light)
- For n=4:
λ4=18004=450 nm(visible, violet light)
8. Conclusion:
- The color of the utensils made from this sheet will appear violet due to the wavelength of light that is constructively interfered being around 450 nm.
- Thickness of the aluminum oxide film, t=250 nm.
- Refractive index of aluminum oxide, n2=1.80.
- Refractive index of air (for simplicity), n1=1.00.
- Light reflecting off a denser medium (from air to aluminum oxide) undergoes a phase change of π (or 180 degrees).
- Light reflecting off a less dense medium (from aluminum oxide to aluminum) does not undergo a phase change, so it remains at 0.
- The total phase difference Δϕ can be calculated as:
Δϕ=ϕ1−ϕ2=π−0=π
- The path difference Δx corresponding to the phase difference of π is given by:
Δx=λ2
- Since we have a film of thickness t, the effective path difference due to the film is:
Δx=2n2t
- Setting the two expressions for path difference equal gives:
2n2t=λ2
- Rearranging gives:
λ=4n2t
- Substitute n2=1.80 and t=250 nm into the equation:
λ=4×1.80×250 nm
λ=1800 nm
- Since 1800 nm is outside the visible spectrum (which ranges from approximately 400 nm to 700 nm), we need to consider the constructive interference for lower orders.
- The first visible wavelength can be calculated by considering n=1 and n=2:
- For n=1:
λ1=18001=1800 nm(not visible)
- For n=2:
λ2=18002=900 nm(not visible)
- For n=3:
λ3=18003=600 nm(visible, red light)
- For n=4:
λ4=18004=450 nm(visible, violet light)
- The color of the utensils made from this sheet will appear violet due to the wavelength of light that is constructively interfered being around 450 nm.
Topper's Solved these Questions
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Exercise 2.2
Explore 22 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Subjective
Explore 11 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Solved Examples
Explore 10 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:single correct Ansewer type
Explore 12 Videos
Similar Questions
A thin transparent film of thickness 3000 Å and refractive index 1.5 ud deposited on a sheet made of a metal. Assuming normal incidence of light and also that the film is a plane parallel one, what will be the color of a pot made from this sheet when observed in white light?
View SolutionA thin film of thickness t and index of refractive 1.33 coats a glass with index of refraction 1.50.What is the least thickness t that will strong reflect light with wavelength 600nm incident normally?
View SolutionA material having an index of refraction of 1.30 is used as an antireflective coating on a piece of glass (n = 1.50). What should be the minimum thickness of this film in order to minimize reflection of 500 nm light?
View SolutionA film with index of refraction 1.50 coats a glass lens with index of refraction 1.80. What is the minimum thickness of the thin film that will strongly reflect light with wavelength 600 nm?
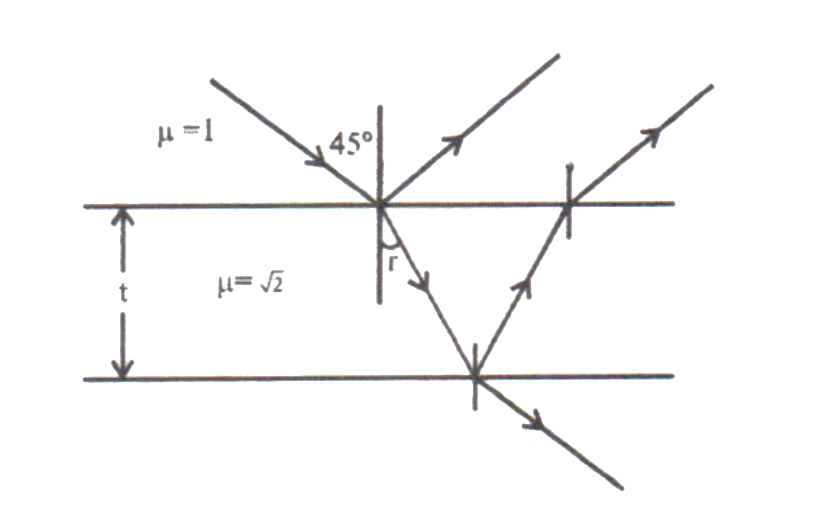
View SolutionA ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
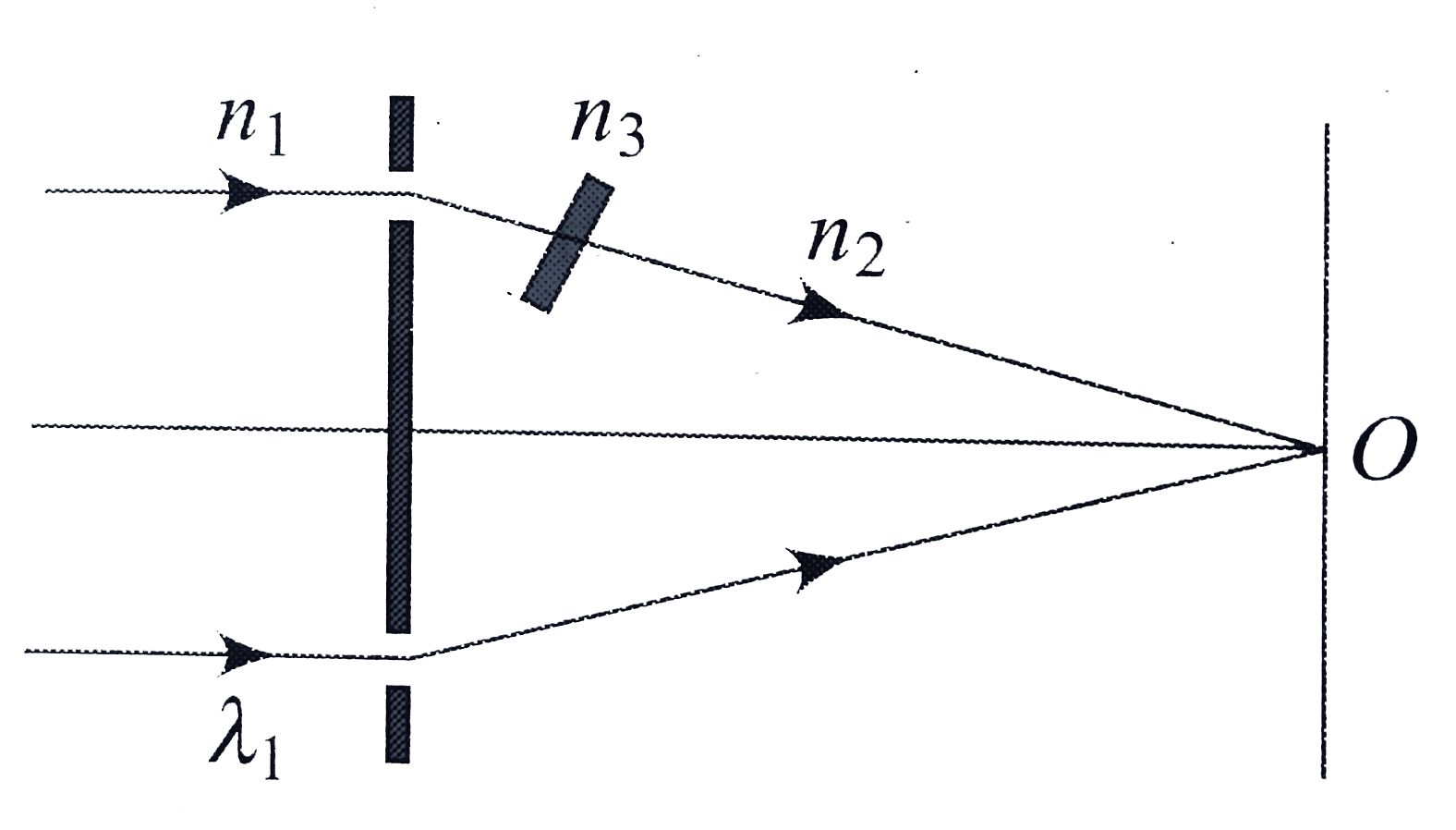
View SolutionIn YDSE shown in figure a parallel beam of light is incident on the slits from a medium of refractive index n1. The wavelength of light in this medium is λ1. A transparent slab of thickness t and refractive index n3 is put in front of one slit. The medium between the screen and the plane of the slits is n2. The phase difference between the light waves reaching point O (symmetrical, relative to the slits) is
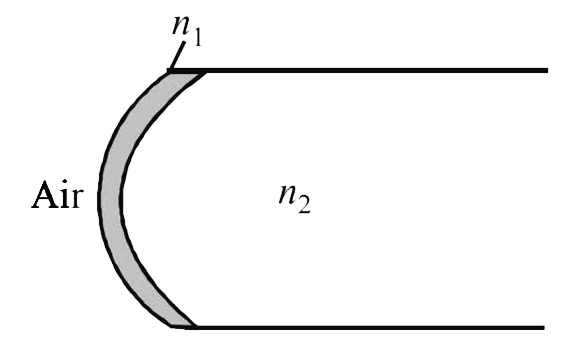
View SolutionA transparent thin film of uniform thickness and refractive index n1=1.4 is coated on the convex spherical surface of radius R at one end of a long solid glass cylinder of refractive index n2=1.5, as shown in the figure. Rays of light parallel to the axis of the cylinder traversing through the film from air to glass get focused at distance f1 from the film, while rays of light traversing from glass to air get focused at distance f2 from the film, Then
View SolutionA glass surface is coated by an oil film of uniform thickness 1.00×10−4cm. The index of refraction of the oil is 1.25 and that of the glass is 1.50. Find the wavelengths of light in the visible region (400nm-750nm) which are completely transmitted by the oil film under normal incidence.
View SolutionA double slit experiment is performed with light of wavelength 500nm. A thin film of thickness 2μm and refractive index 1.5 is introduced in the path of the upper beam. The location of the central maximum will
View SolutionA thin mica sheet of thickness 4×10−6 m and refractive index (μ=1.5) is introduced in the path of the light from upper slit. The wavelength of the wave used is 5000Å The central bright maximum will shift
View Solution