A thin transparent film of thickness 3000 Å and refractive index 1.5 ud deposited on a sheet made of a metal. Assuming normal incidence of light and also that the film is a plane parallel one, what will be the color of a pot made from this sheet when observed in white light?
To determine the color of a pot made from a sheet with a thin transparent film of thickness 3000 Å and refractive index 1.5 when observed in white light, we can follow these steps:
Step 1: Understanding the Conditions
We have a thin film with:
- Thickness (t) = 3000 Å = 3000 × 10^(-10) m = 3 × 10^(-7) m
- Refractive index (μ) = 1.5
- Light incidence is normal.
Step 2: Calculate the Wavelengths for Maxima
For constructive interference (maxima), the condition is given by:
2μt=(n−1)λ2
Where n is an integer (1, 2, 3,...).
Rearranging gives:
λ=4μtn−1
Substituting the values:
λ=4×1.5×3000×10−10n−1
Calculating for different values of n:
1. For n=1:
λ1=4×1.5×3000×10−101−1 (undefined)
2. For n=2:
λ2=4×1.5×3000×10−102−1=18000Å
3. For n=3:
λ3=4×1.5×3000×10−103−1=9000Å
4. For n=4:
λ4=4×1.5×3000×10−104−1=6000Å
Step 3: Calculate the Wavelengths for Minima
For destructive interference (minima), the condition is given by:
2μt=nλ
Rearranging gives:
λ=2μtn
Substituting the values:
λ=2×1.5×3000×10−10n
Calculating for different values of n:
1. For n=1:
λ1=2×1.5×3000×10−101=9000Å
2. For n=2:
λ2=2×1.5×3000×10−102=4500Å
3. For n=3:
λ3=2×1.5×3000×10−103=3000Å
Step 4: Identify the Color
Now we have the wavelengths for maxima and minima:
- Maxima: 18000 Å, 9000 Å, 6000 Å
- Minima: 9000 Å, 4500 Å, 3000 Å
Among these, the wavelengths that fall within the visible spectrum (approximately 4000 Å to 7000 Å) are:
- For maxima: 6000 Å (orange-red)
- For minima: 4500 Å (blue-violet)
Since maxima corresponds to constructive interference and has higher intensity, the color observed will be the one corresponding to the maxima.
Conclusion
The color of the pot made from this sheet, when observed in white light, will be orange-red.
---
We have a thin film with:
- Thickness (t) = 3000 Å = 3000 × 10^(-10) m = 3 × 10^(-7) m
- Refractive index (μ) = 1.5
- Light incidence is normal.
For constructive interference (maxima), the condition is given by:
2μt=(n−1)λ2
Where n is an integer (1, 2, 3,...).
λ=4μtn−1
λ=4×1.5×3000×10−10n−1
1. For n=1:
λ1=4×1.5×3000×10−101−1 (undefined)
2. For n=2:
λ2=4×1.5×3000×10−102−1=18000Å
3. For n=3:
λ3=4×1.5×3000×10−103−1=9000Å
4. For n=4:
λ4=4×1.5×3000×10−104−1=6000Å
For destructive interference (minima), the condition is given by:
2μt=nλ
λ=2μtn
λ=2×1.5×3000×10−10n
1. For n=1:
λ1=2×1.5×3000×10−101=9000Å
2. For n=2:
λ2=2×1.5×3000×10−102=4500Å
3. For n=3:
λ3=2×1.5×3000×10−103=3000Å
Now we have the wavelengths for maxima and minima:
- Maxima: 18000 Å, 9000 Å, 6000 Å
- Minima: 9000 Å, 4500 Å, 3000 Å
- For maxima: 6000 Å (orange-red)
- For minima: 4500 Å (blue-violet)
The color of the pot made from this sheet, when observed in white light, will be orange-red.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.2
22 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Solved Examples
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
By an anodizing process, a transparent film of aluminium oxide of thickness t=250 nm and index of refraction n2=1.80 is deposited on a sheet of polished aluminium What is the color of utenslis made from this sheet with observer in white light? Assume normal incidence of the light.
View SolutionA thin mica sheet of thickness 4×10−6 m and refractive index (μ=1.5) is introduced in the path of the light from upper slit. The wavelength of the wave used is 5000Å The central bright maximum will shift
View SolutionIn a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000Å and intensity (10/π) W m−2 is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness 2000Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
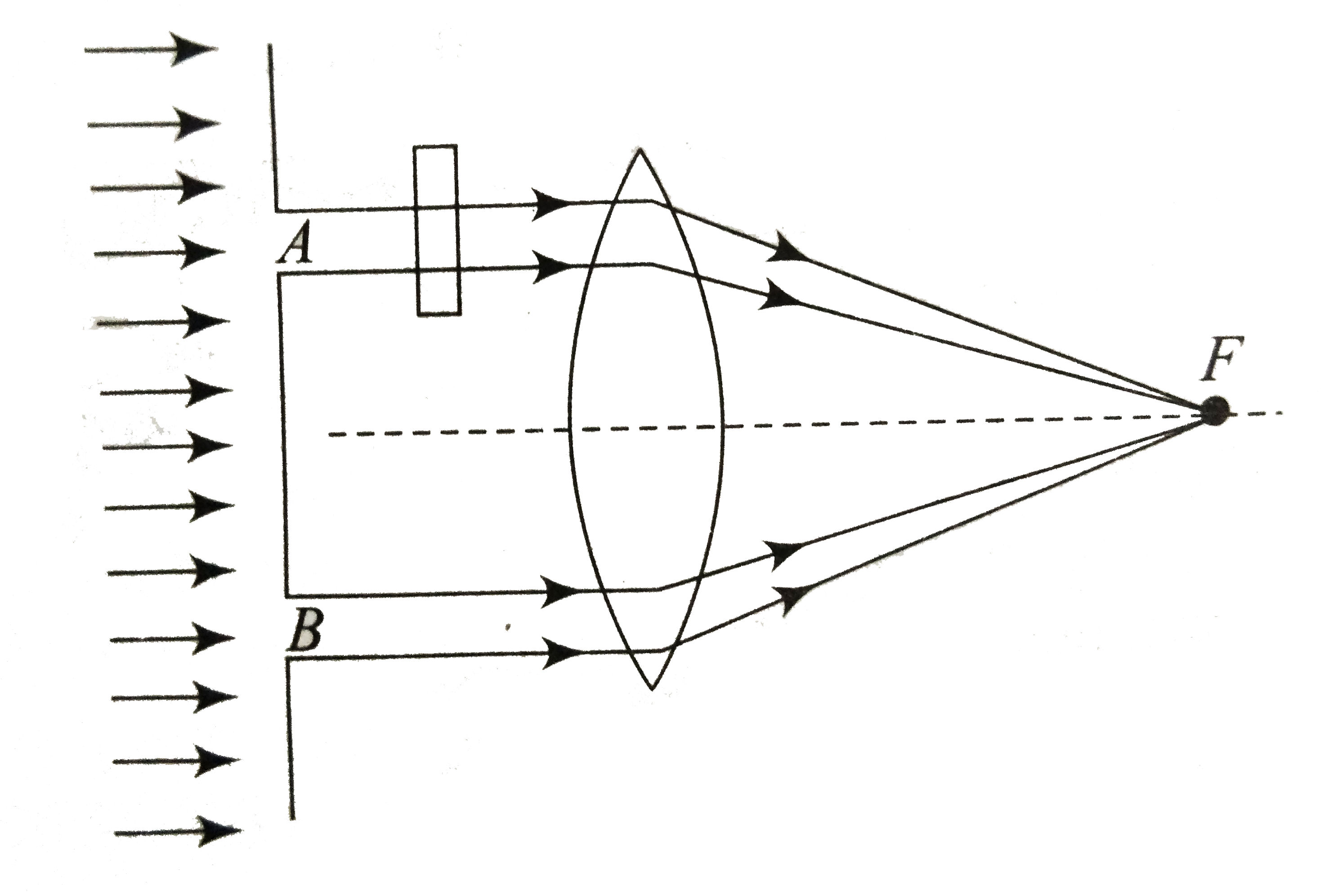
View SolutionInterference pattern with Young's double slits 1.5mm apart are formed on a screen at a distance 1.5m from the plane of slits. In the path of the beam of one of the slits, a transparent film of 10 micron thickness and of refractive index 1.6 is interposed while in the path of the beam from the older slit a transparent film of 15 micron thickness and of refractive index 1.2 is interposed. Find the displacement of the fringe patten.
View SolutionWhen white light is incident normally an oil film of thickness 10−4cm and refractive index. 1.4 then the wavelength which will not be seen in the reflected system of light is
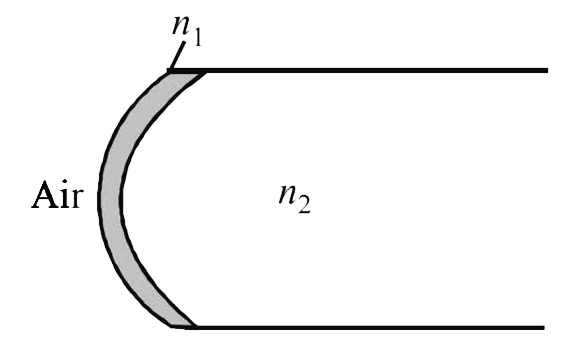
View SolutionA transparent thin film of uniform thickness and refractive index n1=1.4 is coated on the convex spherical surface of radius R at one end of a long solid glass cylinder of refractive index n2=1.5, as shown in the figure. Rays of light parallel to the axis of the cylinder traversing through the film from air to glass get focused at distance f1 from the film, while rays of light traversing from glass to air get focused at distance f2 from the film, Then
View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
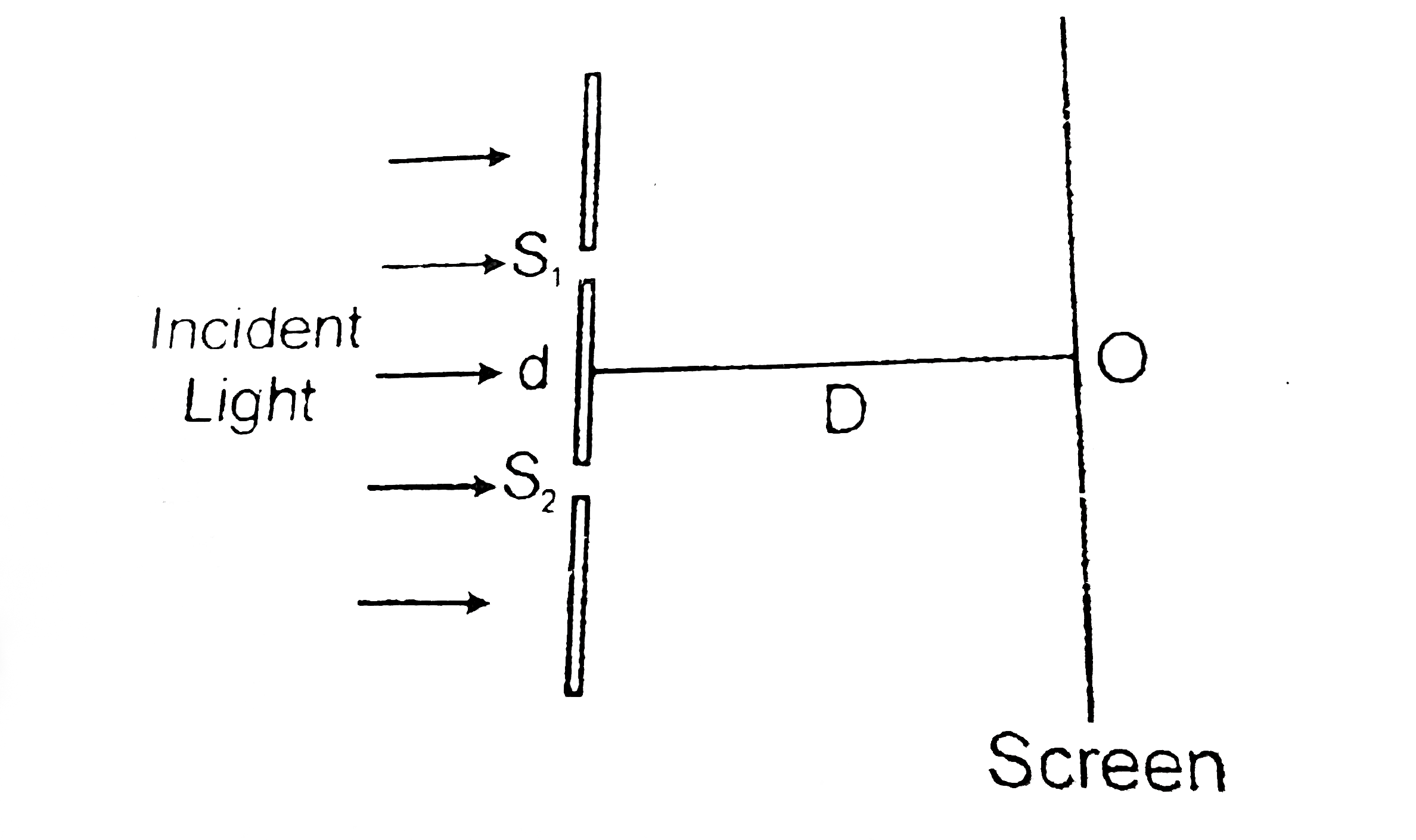
Due to placement of film in front of S1, how many bright fringes cross the point O of screen excluding the one which was at O earlier :
View SolutionA transparent glass plate of thickness 0.5 mm and refractive index 1.5 is placed infront of one of the slits in a double slit experiment. If the wavelength of light used is 6000A∘, the ratio of maximum to minimum intensity in the interference pattern is 25/4. Then the ratio of light intensity transmitted to incident on thin transparent glass plate is
View SolutionIn a doulble slit experiment when a thin film of thickness t having refractive index μ is introduced in from of one of the slits, the maximum at the centre of the fringe pattern shifts by one width. The value of t is (λ is the wavelength of the light used)
View SolutionIn YDSE's experiment performed in a medium of refractive index (4/3), a light of 60 nm wavelength is falling ono the slits having 0.45 mm separation.t he lower slit S2 is covered by a thin glass sheet of thickness 10.4μm and refractive index 1.5 the interference pattern is observed on a screen palced 1.5m from the slits as shown int hef ignore dispersion.
Q. If white light of range 400-700 nm has replaced 600 nm light, one of the wavelengths of light that forms maxima exactly at point O wll be:

View Solution
