Figure shows a YDSE setup having identical slits and with d =5 mm and D = 1 m. A monochromatic light of wavelength is incident on the plane of slit due to which at screen centre O, an intensity is produced with fringe pattern on both sides Now a thin transparent film of thickness and refractive index is placed in front of slit and now interference patten is observed again on screen.
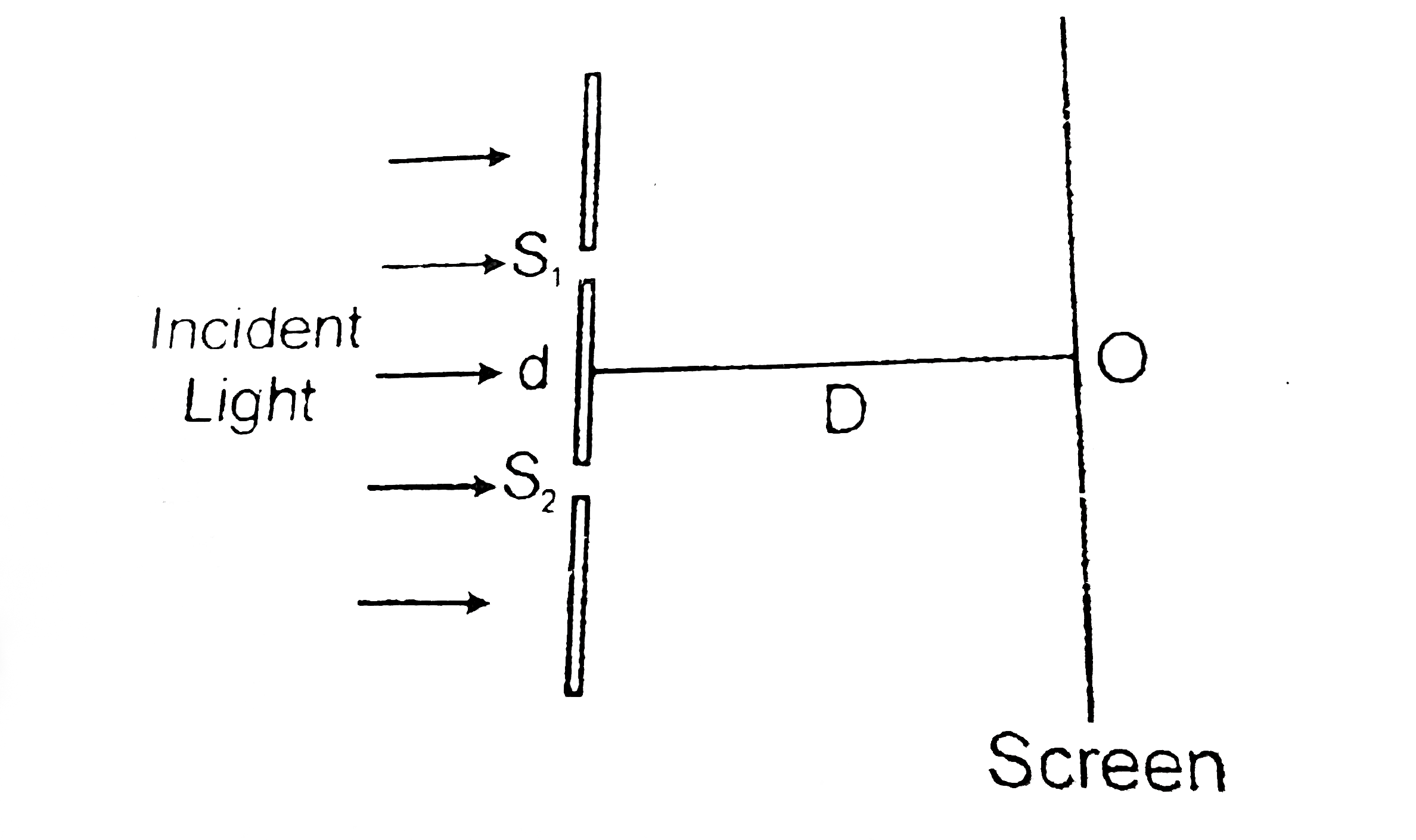
Due to placement of film in front of , how many bright fringes cross the point O of screen excluding the one which was at O earlier :
20
21
42
none of these
The correct Answer is:A
After introducing the film, path difference at point O is
Phase difference at point O is
Thus intensity at point O is
Now path difference at point in terms of is
Thus due to placement of thin film 20 bright fringes cross the point O.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.58
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.59
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.56
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Figure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
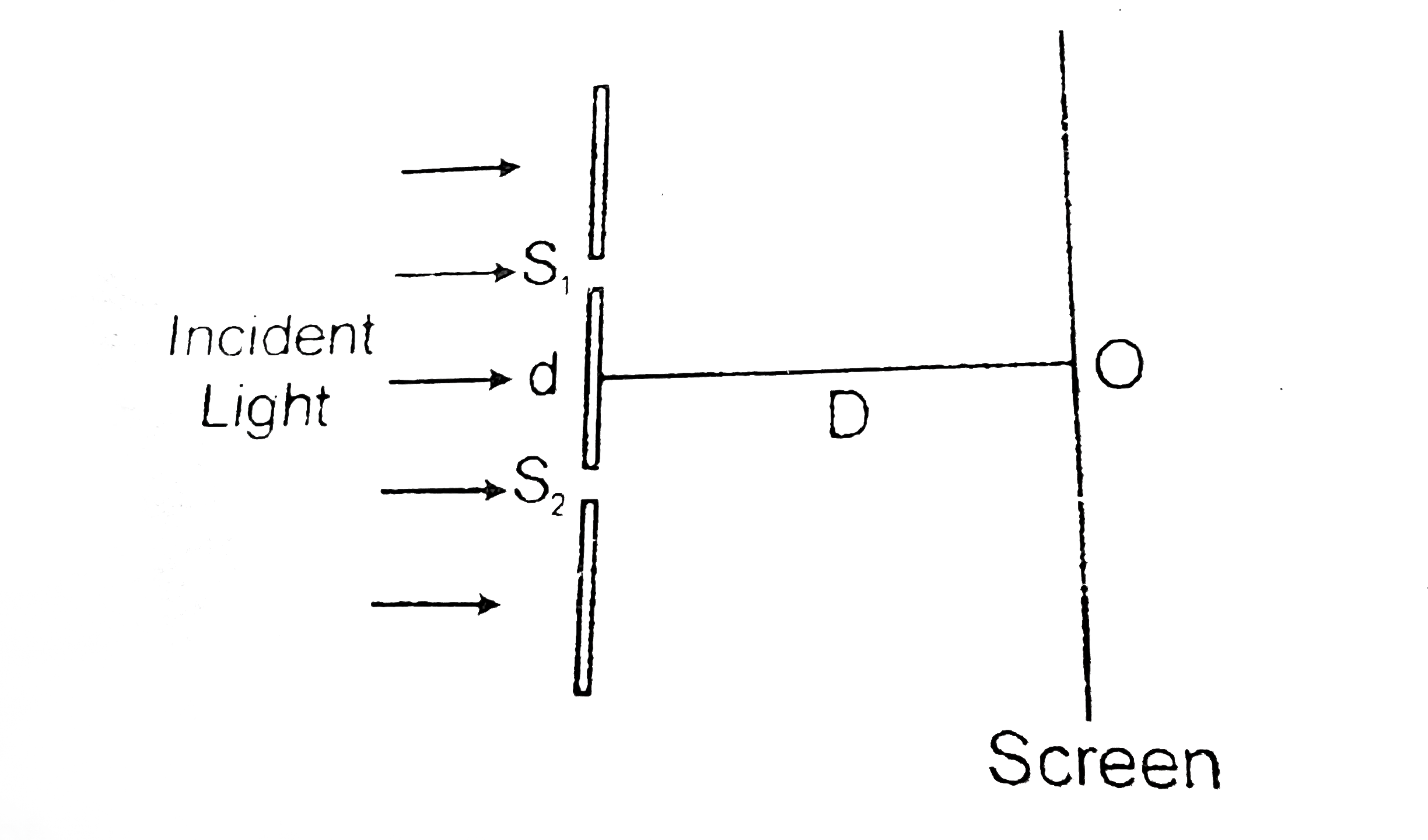
After placing the film of slit S1, the intensity at point O screen is :
View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.

After placing the film of slit S1, the intensity at point O screen is :
View SolutionLight of wavelength 5000Å is incident over a slit of width 1μm. The angular width of central maxima will be
View SolutionMonochromatic light of wavelength 580 nm is incident on a slit of width 0.30 mm. The screen is 2m from the slit . The width of the central maximum is
View SolutionA monochromatic light of λ=5000Å is incident on two identical slits separated by a distance of 5×10−4 m. The interference pattern is seen on a screen placed at a distance of 1 m from the plane of slits. A thin glass plate of thickness 1.5×10−6 m and refractive index μ=1.5 is placed between one of the slits and the screen . Find the intensity at the center of the screen.
View SolutionLight of wavelength 6000Å is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. Find (a) the position of the first dark fringe and (b). The width of the central bright fringe.
View SolutionIn YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
View SolutionYoung's double slit experiment is conducted in a liquid of refractive index μ1 as shown in figure. A thin transparent slab of refractive index μ2 is placed in front of the slit s2. The magnitude of optical path difference at 'O' is
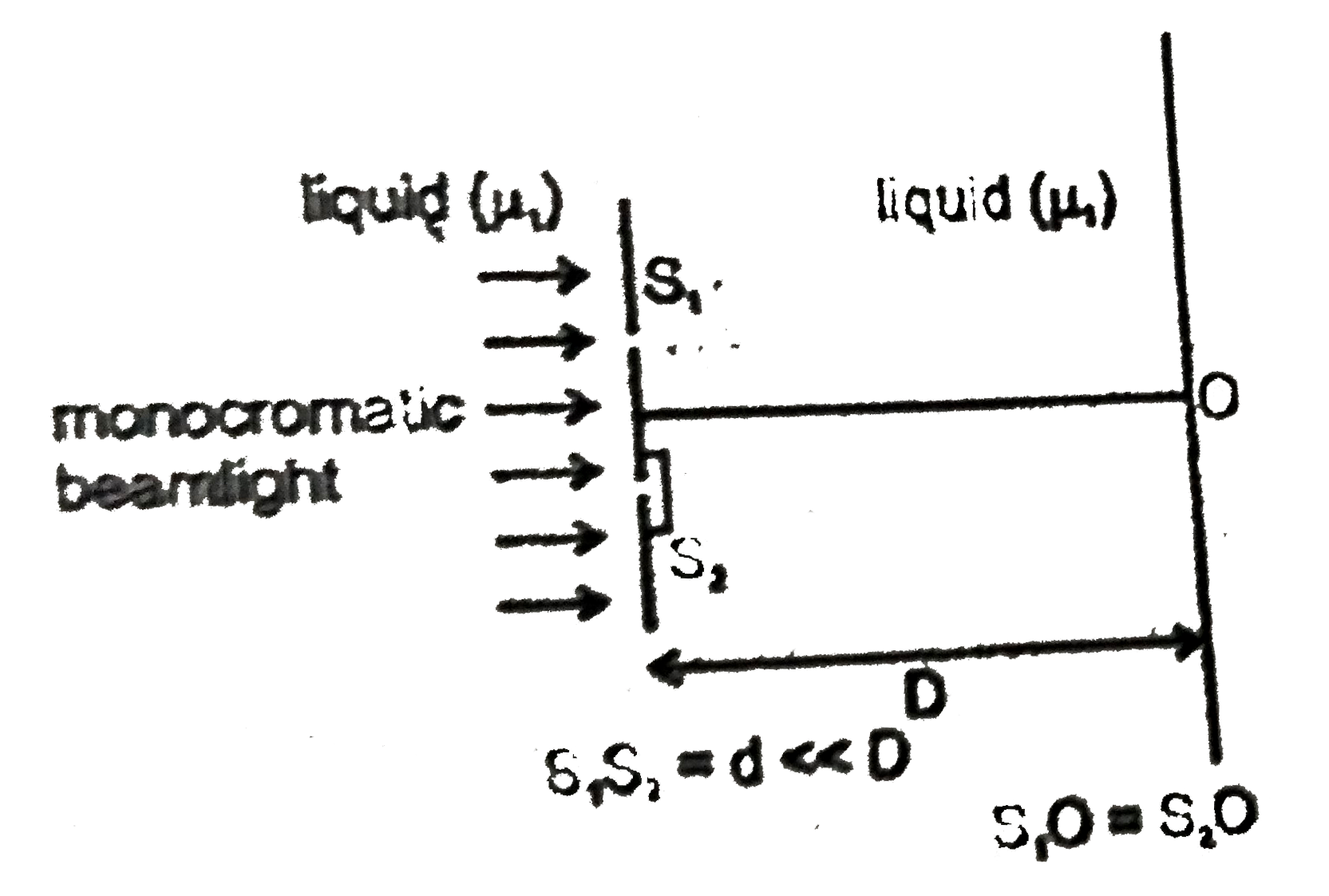
View SolutionIn a doulble slit experiment when a thin film of thickness t having refractive index μ is introduced in from of one of the slits, the maximum at the centre of the fringe pattern shifts by one width. The value of t is (λ is the wavelength of the light used)
View SolutionTwo slits in YDSE are placed 1 mm from each other. Interference pattern is observed on a screen placed 1m from the plane of slits. What is the angular fringe width for a light of wavelength 400 nm
View Solution
