Figure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
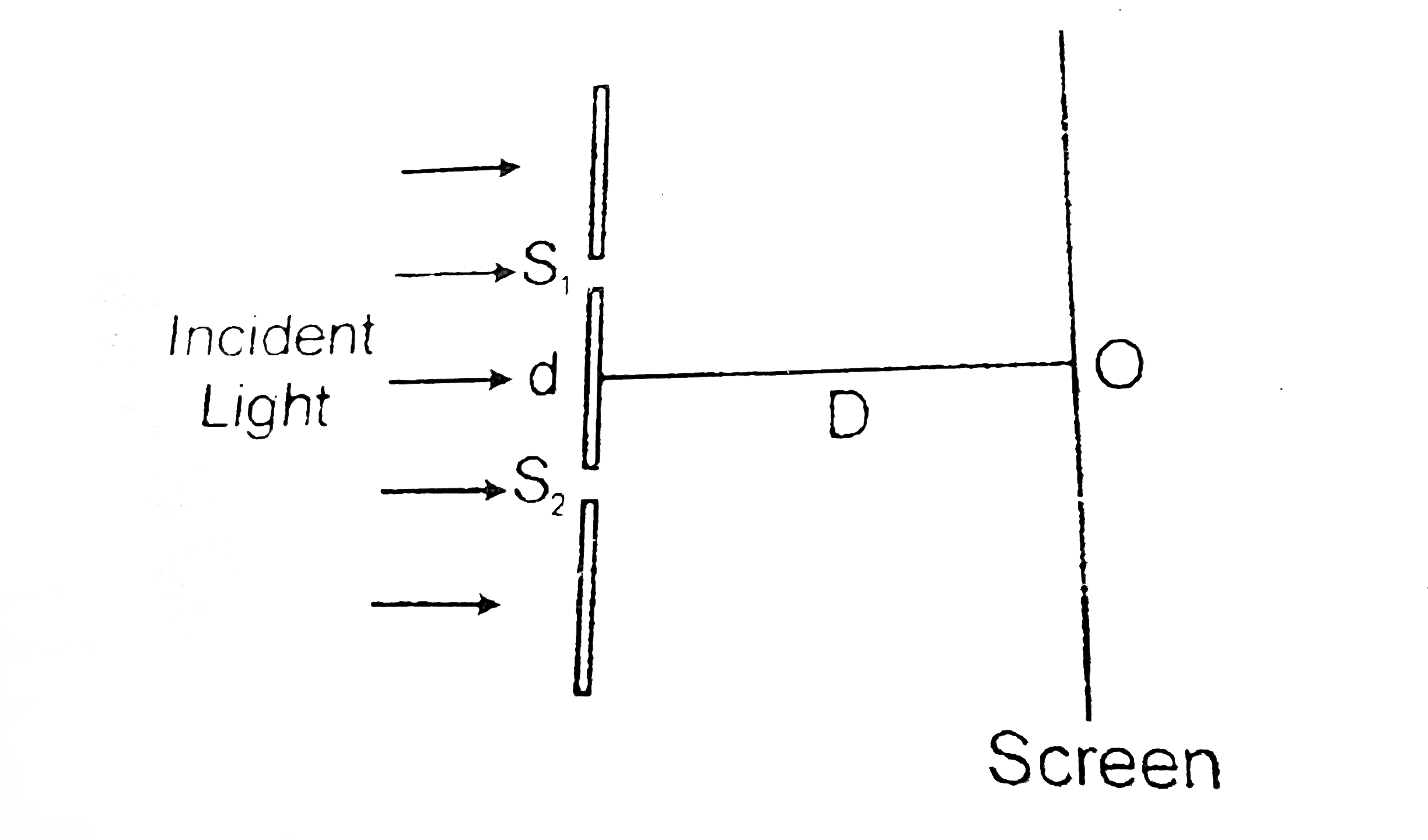
After placing the film of slit S1, the intensity at point O screen is :
I0
3I0/4
I0/2
none of these
The correct Answer is:B
After introducing the film, path difference at point O is
Δ=t(μ−1)=11×10−6×1.1=12.1×10−6m
Phase difference at point O is
ϕ=2πλ×Δ
=2π6×10−712.1×10−6
=12.1π3=π3
Thus intensity at point O is
I=I0cos2ϕ2=I0cos2π6=3I04
Now path difference at point in terms of λ is
Δ0=12.1×10−66×10−7λ=20.167λ
Thus due to placement of thin film 20 bright fringes cross the point O.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.58
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.59
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.56
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
In the circuit shown in fig. XC=100Ω,(XL)=200ΩandR=100Ω. The effective current through the source is

View SolutionConsider a gravity free hall in which an experimenter of mass 50 kg is resting on a 5 kg pillow, 8 ft above the floor of the hall. He pushes the pillow down so that it starts falling at a speed of 8 ft/s. The pillow makes a perfectly elastic collision with the floor, rebounds and reaches the experimenter\'s head. Find the time elapsed in the process.
View SolutionIf E denotes of electric field, the dimension of a quantity ∈0dEdt are those of
View SolutionA galvanometer having 30 divisions has a current sensitivity of 20μA/ division. It has a resistance of 5Ω How will you convert it into an ammeter measuring upto 1A ?
View SolutionAn electromagnetic wave of frequency υ=3 MHz passes from vacuum into a dielectric medium with permittivity ε=4. Then
View SolutionDetermine what happens to the double slits interference pattern if one of the slits is covered with a thin, transparent film whose thickness is lambda/(2(mu-1)) , where lambda is the wavelength of the incident light and mu is the index of refraction of the film.
View SolutionA monochromatic beam of light of 6000 Å is used in YDSE set-up. The two slits are covered with two thin films of equal thickness t but of different refractive indices as shown in figure. Considering the intensity of the incident beam on the slits to be I_(0) , find the point on the screen at which intensity is I_(0) and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.) Consider t = 6 mu m, d = 1 mm, and D = 1 m, where d and D have their usual meaning. Give your answer in mm.
View SolutionIn YDSE monochromatic light of wavelength 600 nm incident of slits as shown in figure.
_PHY_E01_002_Q01.png)
If S1S2=3mm,OP=11mm then
View SolutionA monochromatic light of λ=500nm is incident on two identical slits separated by a distance of 5×10−4m. The interference pattern is seen on a screen placed at a distance of 1m from the plane of slits. A thin glass plate of thickness 1.5×10−6m and refractive index μ=1.5 is placed between one of the slits and the screen. Find the intensity at the centre of the screen if the intensity is I0 in the absence of the plate. Also find the lateral shift of the central maxima and number of fringes crossed through centre.
View Solution_S01_025_Q01.png)
In Young's double slit experiment the slits, S1&S2 are illuminated by a parallel beam of light of wavelength 4000 Å from the medium of refractive index n1=1.2 A thin film of thickness 1.2 μm and refractive index n=1.5 is placed infrom of S1 perpedicular to path of light. the refractive index of medium between plane of slits & screen is n2=1.4 if the light coming from the film and S1&S2 have equal intensities I then intensity at geometrical centre of the screen O is
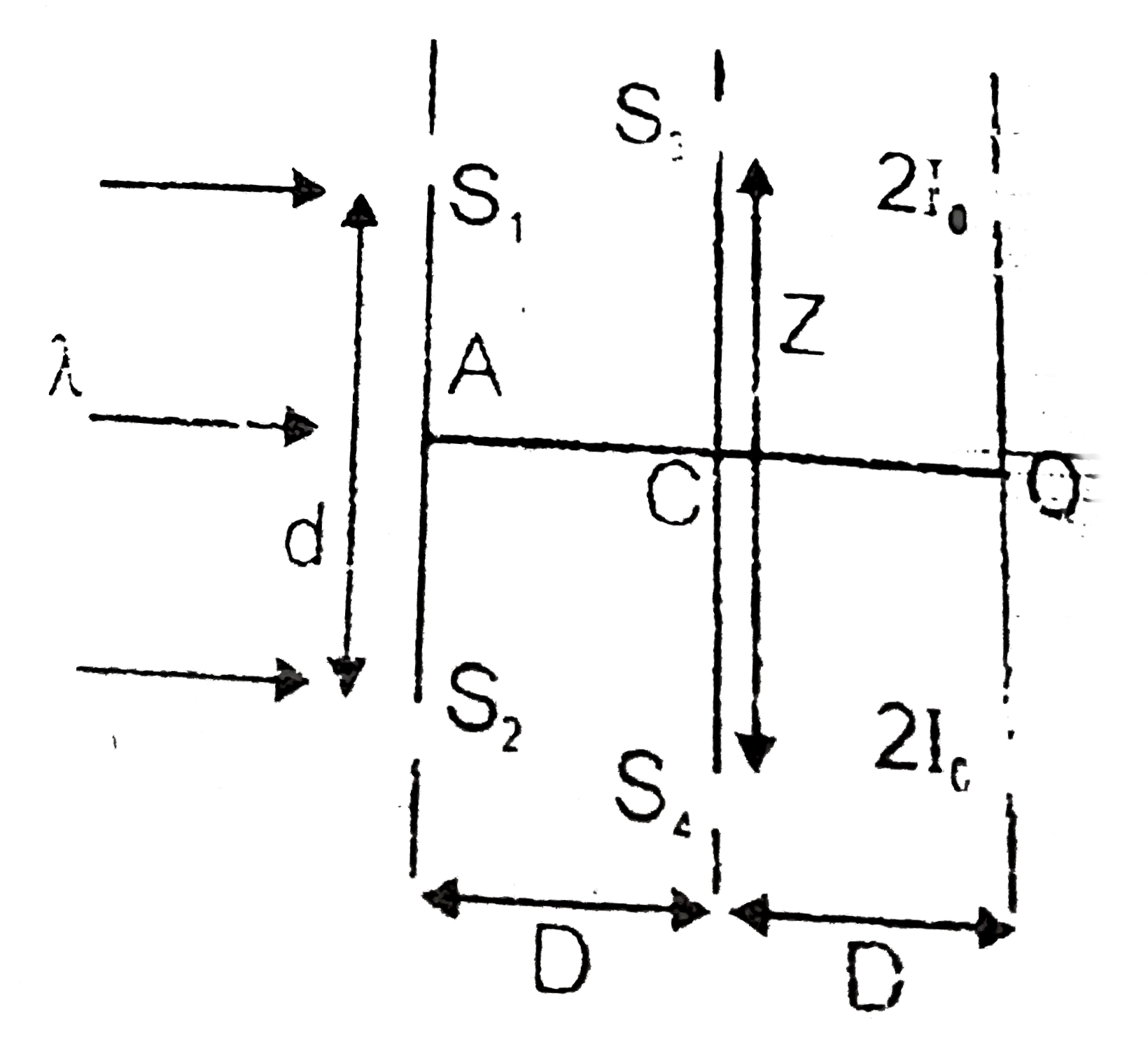
View SolutionIn arrangement shown in figure, plane wavefront of monochromatic light of wavelength λ is incident on identical slits S1 and S2. There is another pair of indentical slits S3 and S4 which are having separation Z=λD2d Point O is on the screen at the common perpendicular bisector of S1S2 and S3S4.I1 is the intensity at point O Now the board having slits S3S4 is moved upward parallel to itself and perpendicular to line AO till slit S4 is on line AO and it is observed that now intensity at point O is I2 then I2I1 is :
View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.

After placing the film of slit S1, the intensity at point O screen is :
View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
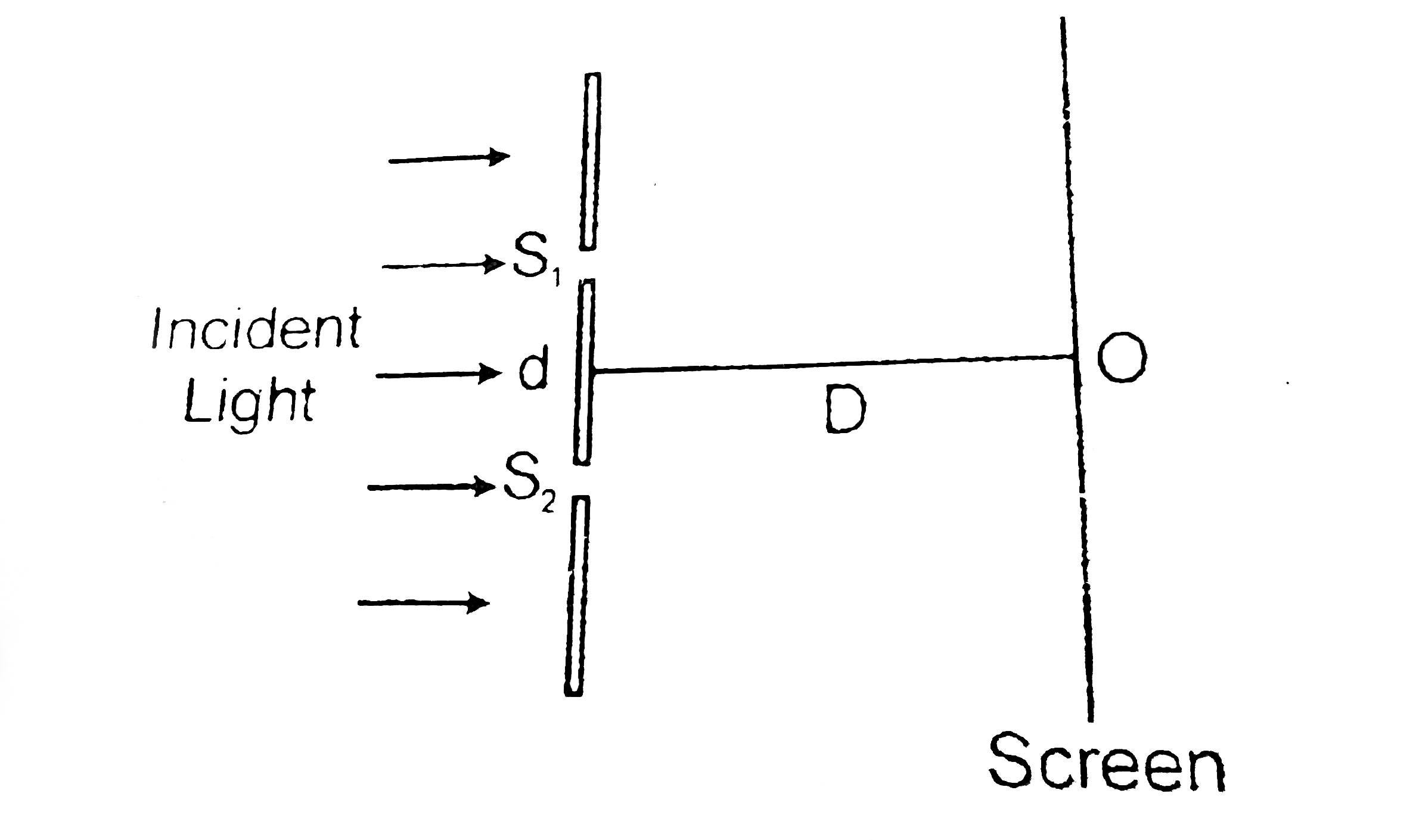
Due to placement of film in front of S1, how many bright fringes cross the point O of screen excluding the one which was at O earlier :
View SolutionA YDSE setup is immersed in water (mu = 1.33) . If has slit separation 1 mm and distance between slits and screen is 1.33m. Incident light on slits have wavelength 6300Å . Find the fringe width on screen.
View SolutionA monochromatic light of wavelength 5000Å incident normally on slit plane of YDSE setup. If d=5×10−4m and D = 1 m and a thin film thickness 1.5×10−6m and μ=1.5 is place in front of one of the slits, find intensity of light at the centre of screen if each slit produces an intensity I0 on screen. [0]
View SolutionThe young's double slit experiment is done in a medium of refractive index 4/3 . A light of 600 nm wavelength is falling on the slits having 0.45 mm separation. The lower slit S_(2) is covered by a thin glass sheet of thickness 10.4 mu m and refractive index 1.5. The interference pattern is observed on a screen placed. 1.5 m from the slit as shown in figure. Find the light intensity at point O relative to the maximum fringe intensity
View Solution
