Determine what happens to the double slits interference pattern if one of the slits is covered with a thin, transparent film whose thickness is , where is the wavelength of the incident light and mu is the index of refraction of the film.
Path difference produced by slab,
path difference is equivalent to phase
difference. Hence, maxima and minima
interchange their positions.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Subjective Questions
5 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Single Correct
11 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Objective question
2 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
Figure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
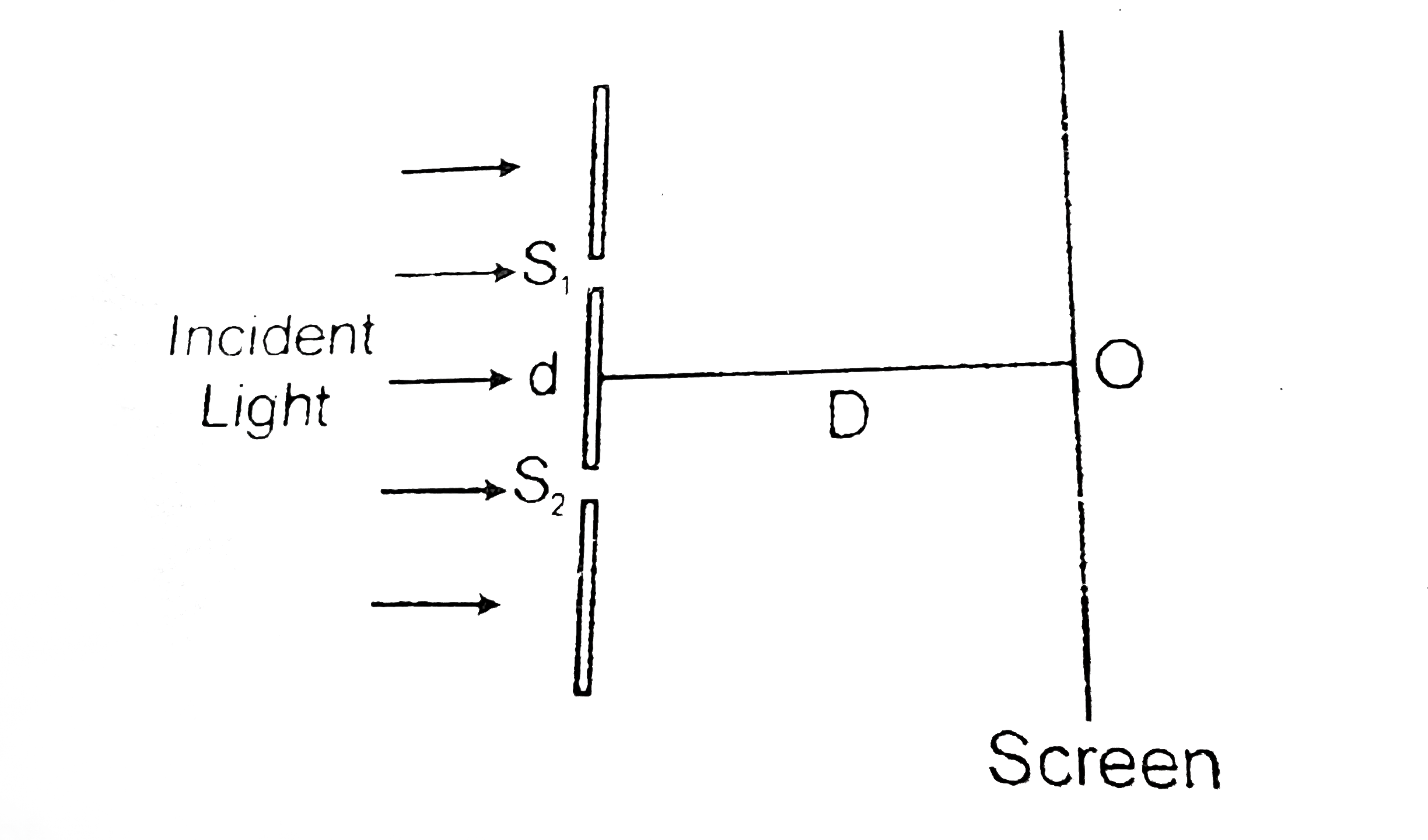
After placing the film of slit S1, the intensity at point O screen is :
View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.

After placing the film of slit S1, the intensity at point O screen is :
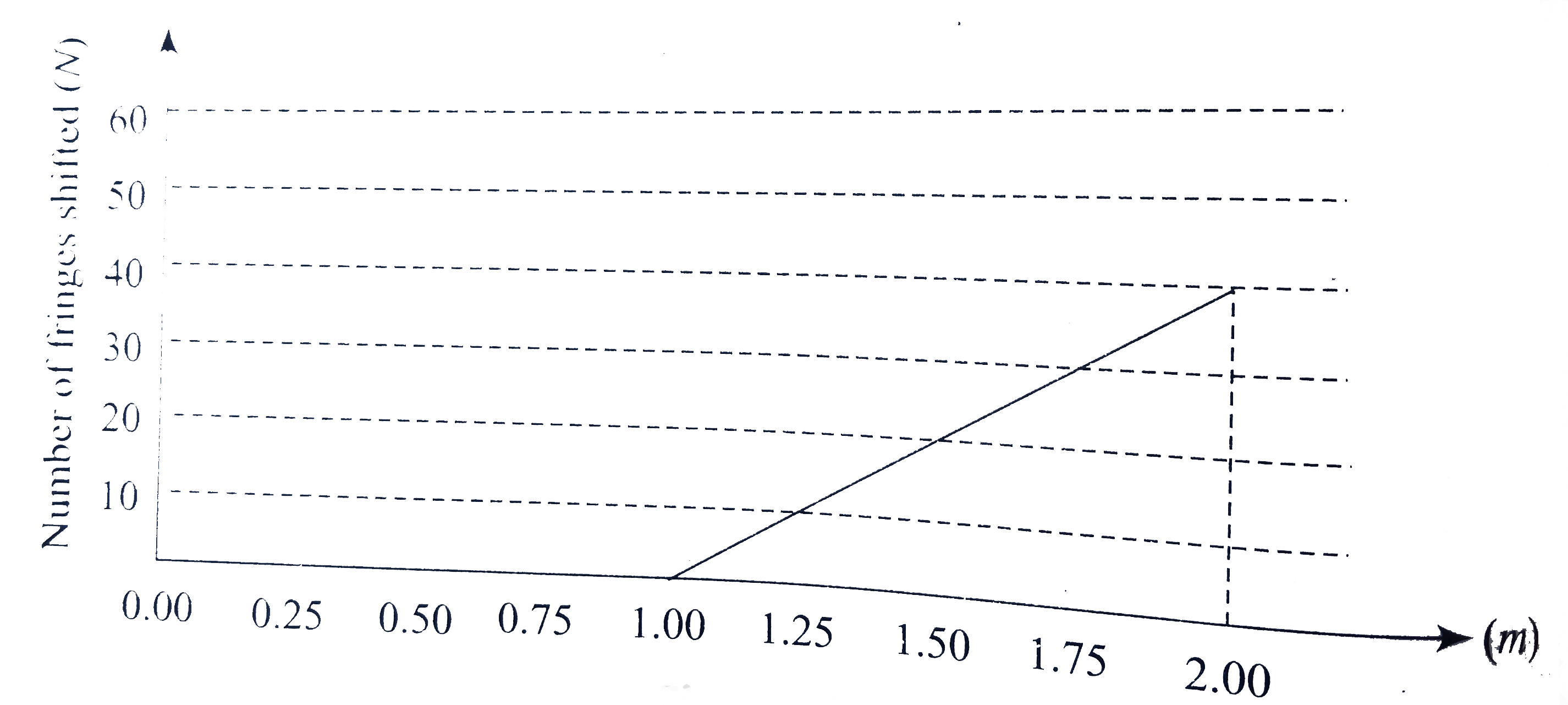
View SolutionThe slits in a double-slit interference experiment are illuminated by orange light (λ=60nm). A thin transparent plastic of thickness t is placed in front of one of the slits. The nunber of fringes shifting on screen is plotted versus the refractive index μ of the plastic in graph shown in figure. The value of t is
View SolutionInterference pattern with Young's double slits 1.5mm apart are formed on a screen at a distance 1.5m from the plane of slits. In the path of the beam of one of the slits, a transparent film of 10 micron thickness and of refractive index 1.6 is interposed while in the path of the beam from the older slit a transparent film of 15 micron thickness and of refractive index 1.2 is interposed. Find the displacement of the fringe patten.
View SolutionA flake of glass (refractive index 1.5) is placed over one of the opening of a double-slit apparatus. The interference pattern displaced itself through seven successive maxima toward the side where the flake is placed. If wavelength of the light is λ=600nm, then the thickness of the flake is
View SolutionIn a Young's double slit experiment minimum intensity is found to be non-zero. If one of the slits is covered by a transparent film which absorbs 10% of light energy passing through it, then
View SolutionIn the Young's double-slit experiment, the intensity of light at a point on the screen where the path difference is λ is K, (λ being the wavelength of light used). The intensity at a point where the path difference is λ/4 will be
View SolutionThe figure shows a Young's double slit experimental setup. It is observed that when a thin transparent sheet of thickness t and refractive index μ is put front of one of the slits, the central maximum gets shifted by a distance equal to n fringe widths. If the wavelength of light used is λ, t will be :
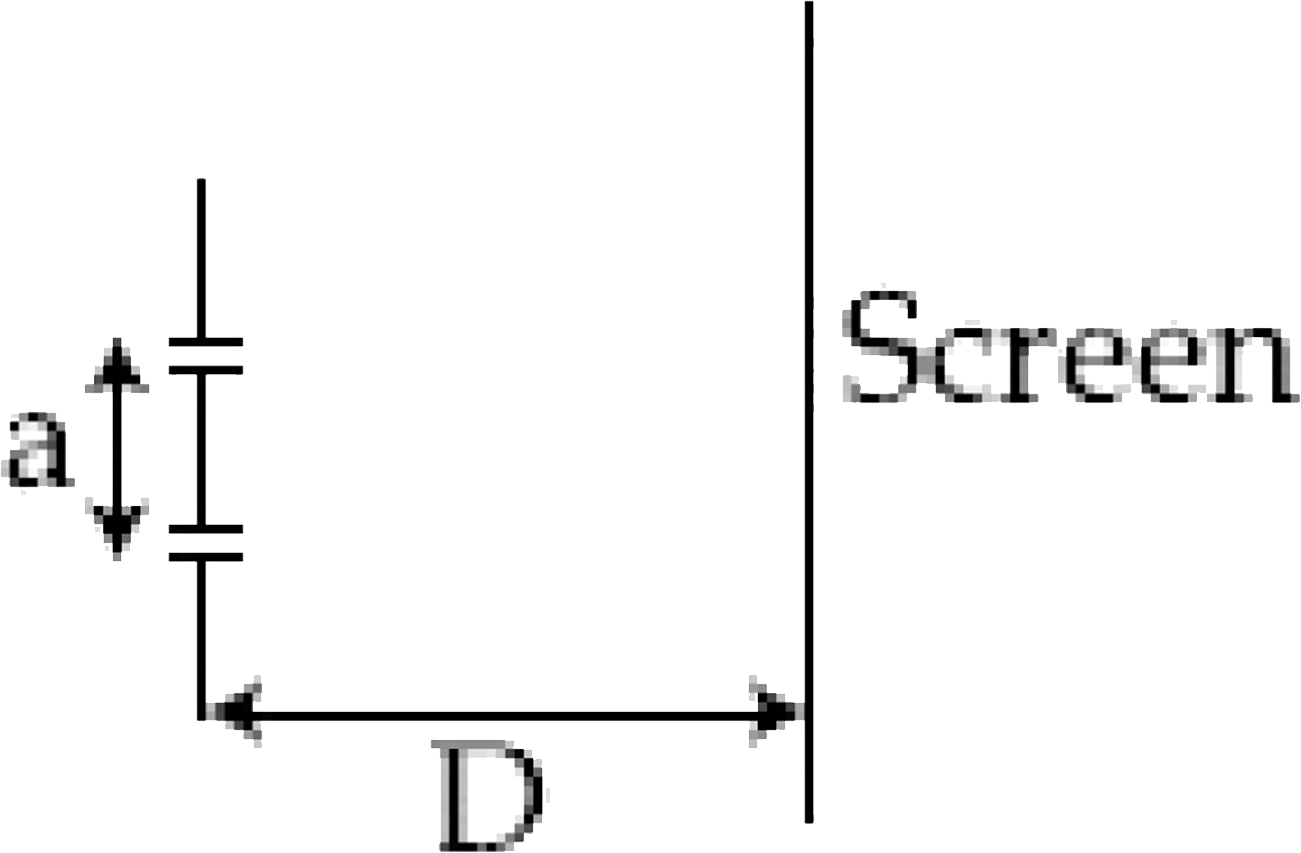
View SolutionFind the minimum thickness of a film which will strongly reflect the light of wavelength 589 nm. The refractive index of the material of the film is 1.25.
View SolutionA Young's double slit interference arrangement with slits S1 and S2, where S2 is immersed in water (refractive index =4/3). Surface of water is exactly between the two slits. The positions of maxima on the surface of water are given by x2=p2m2λ2−d2, where λ is the wavelength of light in air (reflactive index = 1), 2d is the separation between the slits and m is an integer. The value of P is ..........

View Solution
