Blue light of wavelength 480 nm is most strongly reflected off a thin film of oil on a glass slab when viewed near normal incidence. Assuming that the index of refraction of the oil is 1.2 and that of the glass is 1.6, what is the minimum thickness of the oil film (other then zero)?
100 nm
200 nm
300 nm
none
The correct Answer is:b
To solve the problem of finding the minimum thickness of the oil film that causes blue light (wavelength 480 nm) to be most strongly reflected, we can follow these steps:
1. Understand the Setup: We have a thin film of oil on a glass slab, with air above the oil. The indices of refraction are given as:
- noil=1.2
- nglass=1.6
- nair≈1.0
2. Condition for Strong Reflection: For constructive interference (strong reflection) in thin films, the condition is given by:
2μt=nλ
where:
- μ is the refractive index of the film (oil in this case),
- t is the thickness of the film,
- n is the order of interference (for minimum thickness, we take n=1),
- λ is the wavelength of light in vacuum (or air).
3. Wavelength in the Oil: The wavelength of light in the oil can be calculated using the formula:
λoil=λairnoil
where λair=480nm. Thus,
λoil=480nm1.2=400nm
4. Substituting Values: Now, substituting the values into the interference condition for the minimum thickness:
2μt=nλ
becomes:
2×1.2×t=1×400nm
Simplifying this gives:
2.4t=400nm
5. Solving for Thickness t:
t=400nm2.4≈166.67nm
6. Final Answer: The minimum thickness of the oil film (other than zero) is approximately 166.67nm.
Summary of the Calculation:
- The minimum thickness t for strong reflection is calculated using the formula t=nλ2μ.
- Substituting n=1, λ=400nm, and μ=1.2 gives t≈166.67nm.
- noil=1.2
- nglass=1.6
- nair≈1.0
2μt=nλ
where:
- μ is the refractive index of the film (oil in this case),
- t is the thickness of the film,
- n is the order of interference (for minimum thickness, we take n=1),
- λ is the wavelength of light in vacuum (or air).
λoil=λairnoil
where λair=480nm. Thus,
λoil=480nm1.2=400nm
2μt=nλ
becomes:
2×1.2×t=1×400nm
Simplifying this gives:
2.4t=400nm
t=400nm2.4≈166.67nm
- The minimum thickness t for strong reflection is calculated using the formula t=nλ2μ.
- Substituting n=1, λ=400nm, and μ=1.2 gives t≈166.67nm.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
A material having an index of refraction of 1.30 is used as an antireflective coating on a piece of glass (n = 1.50). What should be the minimum thickness of this film in order to minimize reflection of 500 nm light?
View SolutionA glass lens is coated on one side with a thin film of magnesium fluoride (MgF2)to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of MgF2 is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm (λ=550nm)? Assume that the light is approxmately perpendicular to the lens surface.
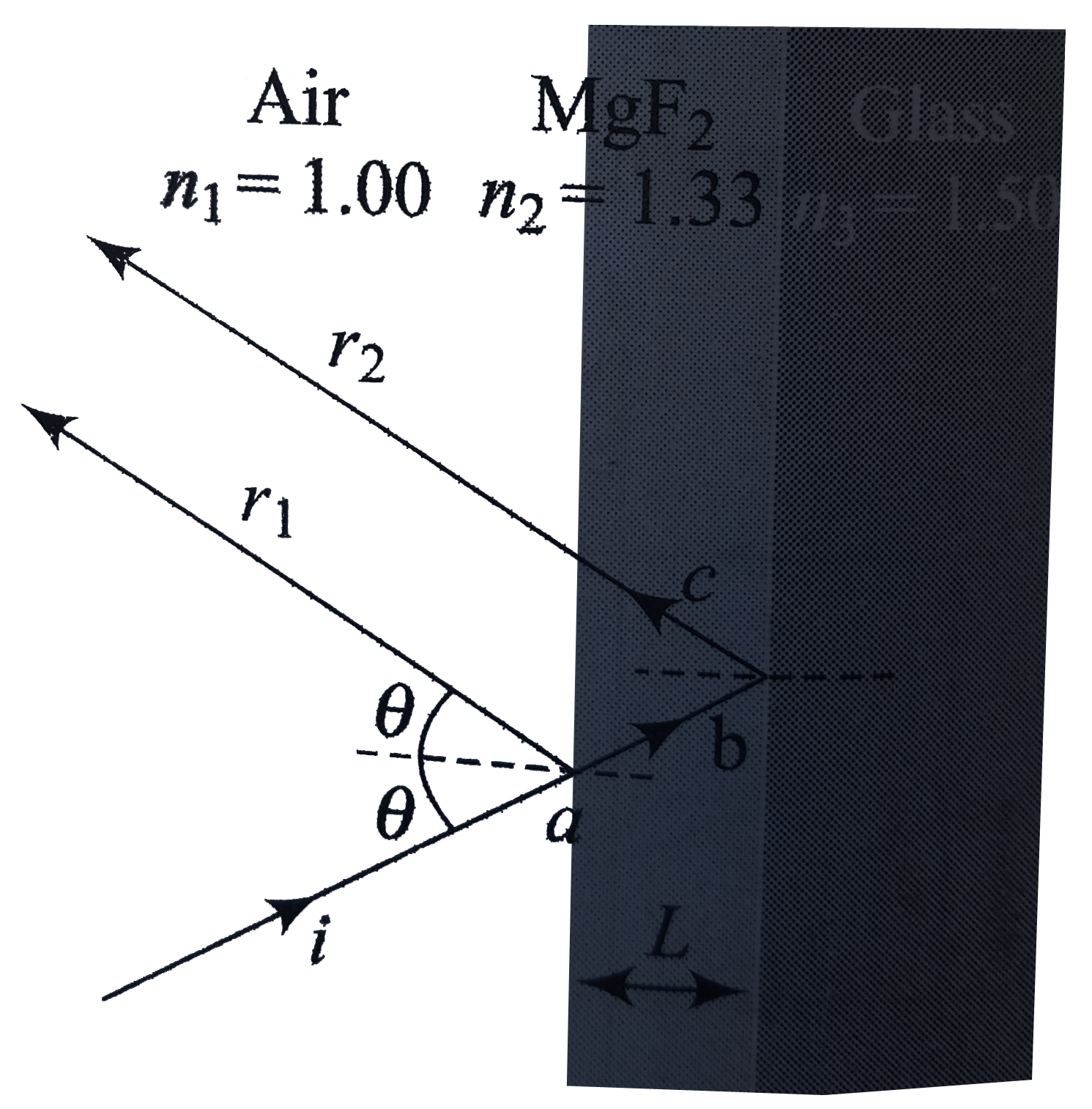
View SolutionA film with index of refraction 1.50 coats a glass lens with index of refraction 1.80. What is the minimum thickness of the thin film that will strongly reflect light with wavelength 600 nm?
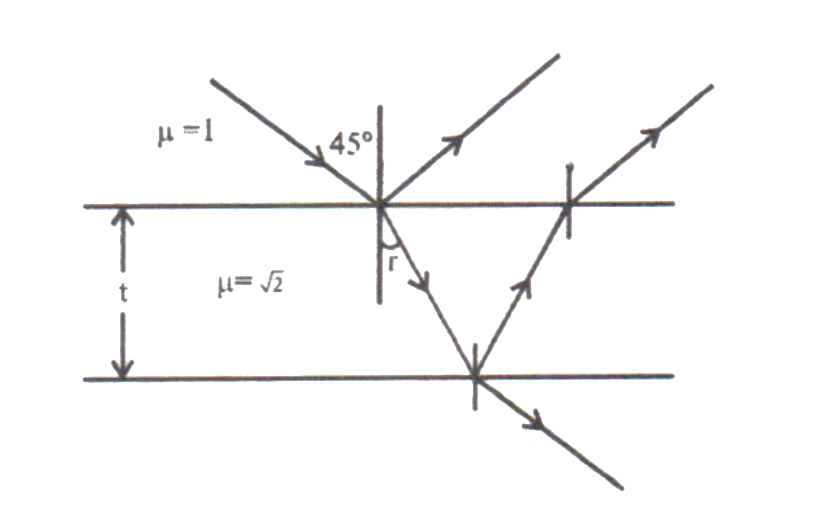
View SolutionA ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
View SolutionA glass surface is coated by an oil film of uniform thickness 1.00×10−4cm. The index of refraction of the oil is 1.25 and that of the glass is 1.50. Find the wavelengths of light in the visible region (400nm-750nm) which are completely transmitted by the oil film under normal incidence.
View SolutionA thin film of soap solution (μs=1.5). When visible light is incident almost normal to the plate, two wavelength 420 nm and 630 nm are strongly reflected. What is the minimum thickness (in nm) of the soap film?
View SolutionLight of wavelength 6000Å is incident on a thin glass plate of refractive index 1.5 such that angle of refraction into the plate is 60∘. Calculate the smallest thickness of plate which will make it appear dark by reflection.
View SolutionAn air bubble in a glass slab with refractive index 1.5 (near normal incidence) is 5cm deep when viewed from one surface and 3cm deep when viewed from the opposite face. The thickness (in cm) of the slab is
View SolutionA parallel beam of light of wavelength 560 nm falls on a thin film of oil (refractive index = 1.4). What should be the minimum thickness of the film so that it strongly transmit the light ?
View SolutionA plane wave of monochromatic light falls normally on a uniform thin or oil which covers a glass plate. The wavelength of source can be varied continuously. Complete destructive is observed for λ=5000Å and λ=1000Å and for no other wavelength in between. If μ of oil is 1.3 and that of glass is 1.5, the thickness of the film will be
View Solution
