A particle is projected up an inclined plane of inclination β at na elevation ∝ to the horizon. Show that tan∝=cotβ+2tanβ, if the particle strikes the plane at right angles
(a) 0=usin(∝−β)t−12gcosβt2
t=2usin(∝−β)gcosβ…(i)
0=ucos(∝−β)−gsinβt
⇒t=ucos(∝−β)gcosβ …(ii)
From (i) and (ii), we get
2sin(∝−β)cosβ=cos(∝−β)sinβ
⇒2tan(∝−β)=cotβ
⇒2(tan∝−tanβ)1+tan∝tanβ=cotβ
⇒2tan∝−2tanβ=cotβ+tan∝
⇒tan∝=cotβ+2tanβ
(b) t=2usin(∝−β)/gcosβ
Also, t=usin∝g
⇒2sin(∝−β)cosβ=sin∝
⇒2sin∝cosβ−2cos∝sinβ=sin∝cosβ
⇒sin∝cosβ=2cos∝sinβ
⇒tan∝=2tanβ.
 ,
, .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A particle is projected up an inclined plane of inclination β at na elevation ∝ to the horizontal. Show that
(a) tan∝=cotβ+2tanβ, if the particle strikes the plane at right angles
(b) tan∝=2tanβ, if the particle strikes the plane horizontally.
View SolutionA particle is projected up an inclined plane of inclination β at an elevation ∝ to the horizontal. Find the ratio between tan∝andtanβ, if the particle strikes the plane horizontally.
View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α (from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View SolutionA particle is projected with a certain velocity at an angle ∝ above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally, then ∝ is equal to.
View SolutionA particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
View SolutionA particle is projected at an angle alpha with horizontal from the foot of a plane whoose inclinaiton to horizontal is β. Shwo that is will strike the plane at right angles if , cotβ=2tan(α−β) .
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionAn inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
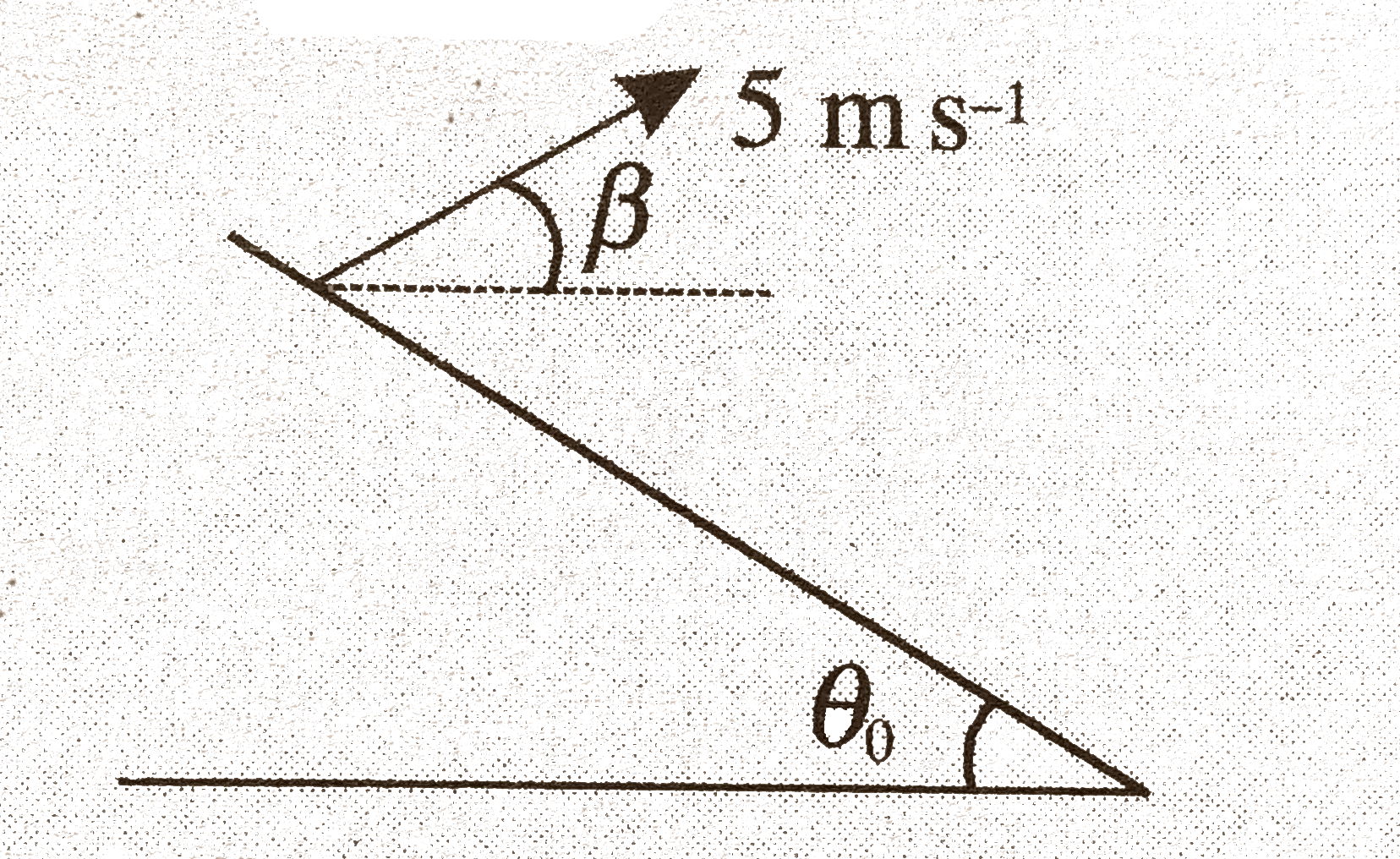 .
.
View Solution
