A particle is projected up an inclined plane of inclination β at na elevation ∝ to the horizontal. Show that
(a) tan∝=cotβ+2tanβ, if the particle strikes the plane at right angles
(b) tan∝=2tanβ, if the particle strikes the plane horizontally.
To solve the problem, we will analyze the motion of a particle projected up an inclined plane at an angle α to the horizontal, and we will derive the required equations for two different scenarios: when the particle strikes the plane at right angles and when it strikes the plane horizontally.
Part (a): Show that tanα=cotβ+2tanβ if the particle strikes the plane at right angles.
1. Identify the Components of Motion:
- The inclined plane makes an angle β with the horizontal.
- The particle is projected at an angle α to the horizontal.
- The velocity components can be broken down into two directions: along the incline and perpendicular to the incline.
2. Time of Flight:
- The time of flight T for a projectile on an inclined plane is given by:
T=2usin(α−β)gcosβ
3. Condition for Striking at Right Angles:
- For the particle to strike the inclined plane at right angles, the horizontal component of the velocity must become zero at the time of impact.
- The horizontal component of the velocity at time T is given by:
vx=ucos(α)−gsin(β)T
- Setting vx=0 gives:
ucos(α)=gsin(β)T
4. Substituting Time of Flight:
- Substitute T into the equation:
ucos(α)=gsin(β)(2usin(α−β)gcosβ)
- Simplifying this, we get:
ucos(α)=2usin(α−β)tan(β)
- Dividing both sides by u (assuming u≠0):
cos(α)=2sin(α−β)tan(β)
5. Using Trigonometric Identities:
- Expanding sin(α−β):
sin(α−β)=sin(α)cos(β)−cos(α)sin(β)
- Substitute this back into the equation:
cos(α)=2(sin(α)cos(β)−cos(α)sin(β))tan(β)
- Rearranging gives:
cos(α)+2cos(α)sin(β)tan(β)=2sin(α)cos(β)tan(β)
- Factor out cos(α):
cos(α)(1+2sin(β)tan(β))=2sin(α)cos(β)tan(β)
6. Final Rearrangement:
- Dividing both sides by cos(β):
tan(α)=2tan(β)1+2sin(β)tan(β)
- This leads to the final result:
tan(α)=cot(β)+2tan(β)
Part (b): Show that tanα=2tanβ if the particle strikes the plane horizontally.
1. Condition for Striking Horizontally:
- For the particle to strike the inclined plane horizontally, the vertical component of the velocity must be zero at the time of impact.
- The time of flight for a projectile is given by:
T=usin(α)g
2. Equating Time of Flight:
- For horizontal projection, the time of flight is also given by:
T=usin(α−β)gcos(β)
- Setting these equal gives:
usin(α)g=usin(α−β)gcos(β)
- Simplifying this leads to:
sin(α)cos(β)=sin(α−β)
3. Using Trigonometric Identities:
- Expanding sin(α−β):
sin(α−β)=sin(α)cos(β)−cos(α)sin(β)
- Substitute this back into the equation:
sin(α)cos(β)=sin(α)cos(β)−cos(α)sin(β)
- Rearranging gives:
cos(α)sin(β)=0
4. Conclusion:
- Since sin(β)≠0 (as β is the angle of inclination), we conclude that:
tan(α)=2tan(β)
- The inclined plane makes an angle β with the horizontal.
- The particle is projected at an angle α to the horizontal.
- The velocity components can be broken down into two directions: along the incline and perpendicular to the incline.
- The time of flight T for a projectile on an inclined plane is given by:
T=2usin(α−β)gcosβ
- For the particle to strike the inclined plane at right angles, the horizontal component of the velocity must become zero at the time of impact.
- The horizontal component of the velocity at time T is given by:
vx=ucos(α)−gsin(β)T
- Setting vx=0 gives:
ucos(α)=gsin(β)T
- Substitute T into the equation:
ucos(α)=gsin(β)(2usin(α−β)gcosβ)
- Simplifying this, we get:
ucos(α)=2usin(α−β)tan(β)
- Dividing both sides by u (assuming u≠0):
cos(α)=2sin(α−β)tan(β)
- Expanding sin(α−β):
sin(α−β)=sin(α)cos(β)−cos(α)sin(β)
- Substitute this back into the equation:
cos(α)=2(sin(α)cos(β)−cos(α)sin(β))tan(β)
- Rearranging gives:
cos(α)+2cos(α)sin(β)tan(β)=2sin(α)cos(β)tan(β)
- Factor out cos(α):
cos(α)(1+2sin(β)tan(β))=2sin(α)cos(β)tan(β)
- Dividing both sides by cos(β):
tan(α)=2tan(β)1+2sin(β)tan(β)
- This leads to the final result:
tan(α)=cot(β)+2tan(β)
- For the particle to strike the inclined plane horizontally, the vertical component of the velocity must be zero at the time of impact.
- The time of flight for a projectile is given by:
T=usin(α)g
- For horizontal projection, the time of flight is also given by:
T=usin(α−β)gcos(β)
- Setting these equal gives:
usin(α)g=usin(α−β)gcos(β)
- Simplifying this leads to:
sin(α)cos(β)=sin(α−β)
- Expanding sin(α−β):
sin(α−β)=sin(α)cos(β)−cos(α)sin(β)
- Substitute this back into the equation:
sin(α)cos(β)=sin(α)cos(β)−cos(α)sin(β)
- Rearranging gives:
cos(α)sin(β)=0
- Since sin(β)≠0 (as β is the angle of inclination), we conclude that:
tan(α)=2tan(β)
Similar Questions
A particle is projected up an inclined plane of inclination β at na elevation ∝ to the horizon. Show that tan∝=cotβ+2tanβ, if the particle strikes the plane at right angles
View SolutionA particle is projected up an inclined plane of inclination β at an elevation ∝ to the horizontal. Find the ratio between tan∝andtanβ, if the particle strikes the plane horizontally.
View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α (from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View SolutionA particle is projected with a certain velocity at an angle ∝ above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally, then ∝ is equal to.
View SolutionA particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
View SolutionA particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View SolutionA particle is projected at an angle alpha with horizontal from the foot of a plane whoose inclinaiton to horizontal is β. Shwo that is will strike the plane at right angles if , cotβ=2tan(α−β) .
View SolutionAn inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
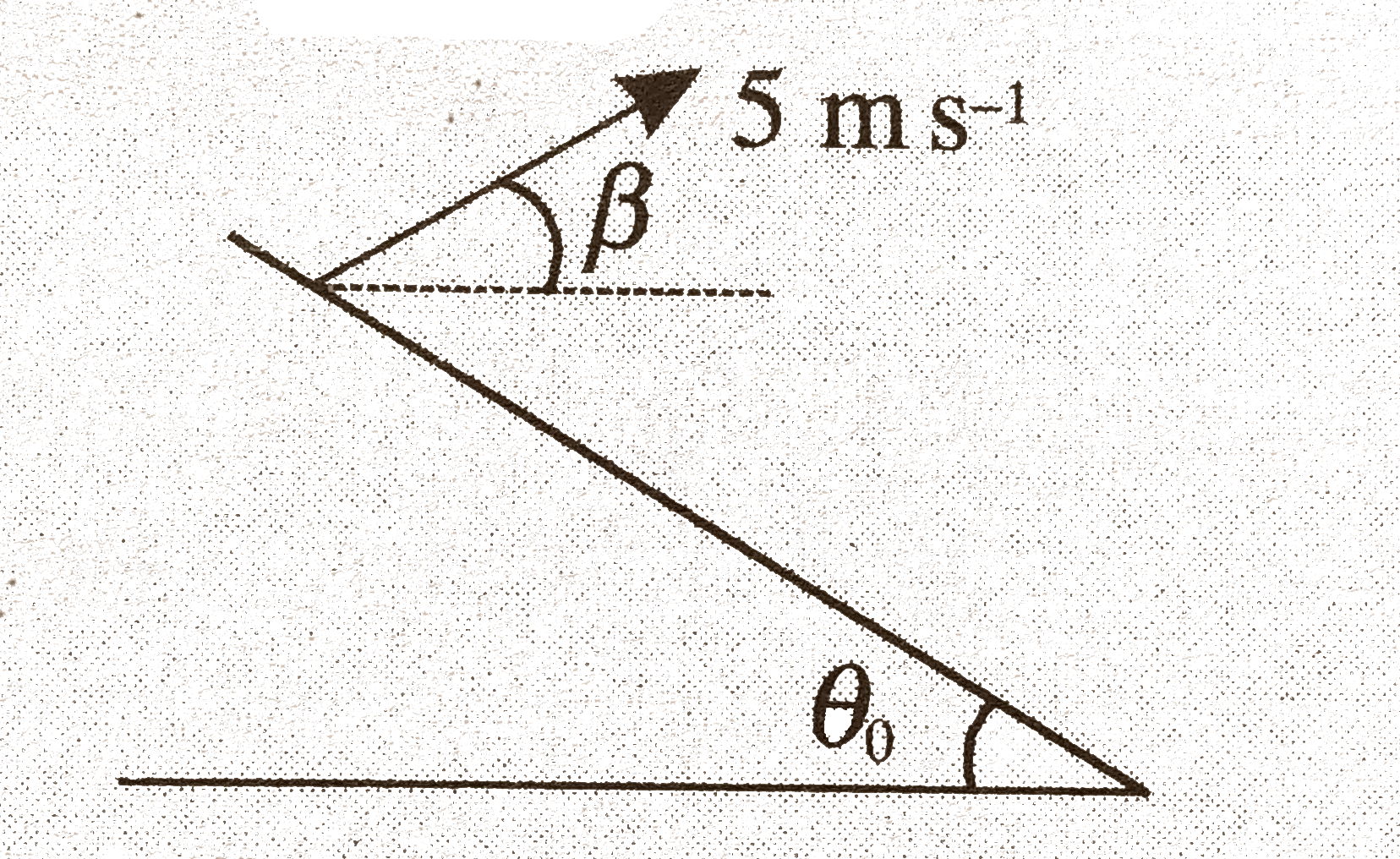 .
.
View Solution

