A particle starts from rest and moves in a circular motion with constant angular acceleration of 2rads−2. Find
(a) Angular velocity
(b) Angular displacement of the particle after 4s.
( c) The number of revolutions completed by the particle during these 4s.
(d) If the radius of the circle is 10cm, find the magnitude and direction of net acceleration of the particle at the end of 4s.
The correct Answer is:(a) 8rads−1;
(b) 16rad;
( c) 2811rev;
(d) tan−1(132).
∝=2rads−2,ω1=0,t=4s
(a) ω2=ω1+∝t⇒ω2=0+2×4=8rads−1
(b) θ=ω1t+12∝t2
⇒θ=0×4+12×2×42=16rad
( c) Irevolution=2πrad⇒1rad=12rev
⇒16rad=162πrev=8πrev=8×722=2811rev
(d) Aftter 4 s : v=ω2r=8×10/100=0.8ms−1
ac=v2r=(0.8)210/100=6.4ms−2
at=∝r=2×10100=0.2ms−2
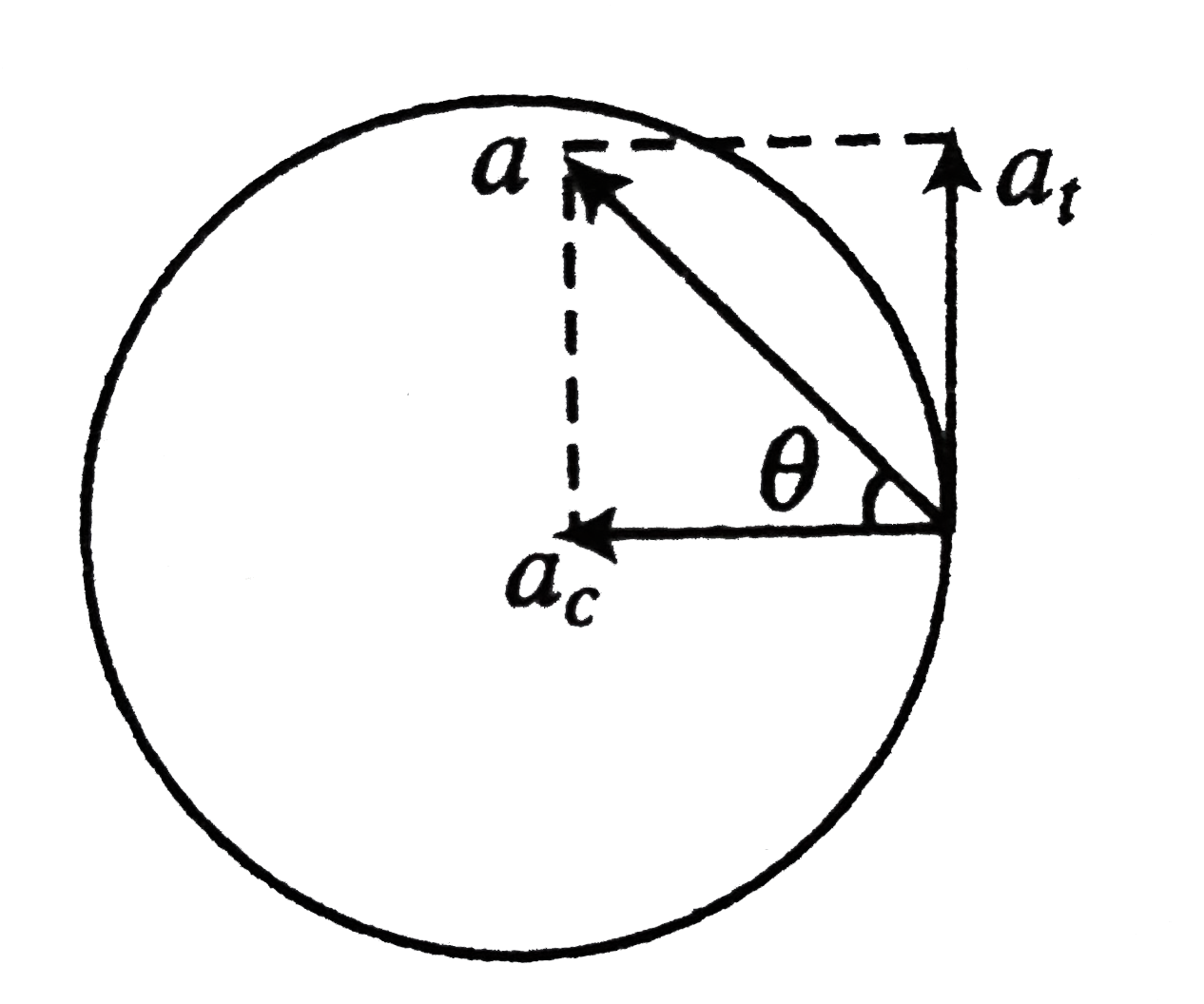
Now magnitude of net acceleration,
a=√a2c+a2t=√6.4+0.22=√41ms−2
Direction of acceleration,
tanθ=atac=0.26.4=132⇒θ=tan−1(132).
 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct76videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct11videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.411videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
View SolutionWhat is the angular acceleration of a particle moving with constant angular velocity ?
View SolutionWhat is the angular acceleration of a particle moving with constant angular velocity ?
View SolutionStarting from rest a wheel rotates with uniform angular acceleration 2πrads−2. After 4s, if the angular acceleration ceases to act, its angular displacement in the next 4s is
View SolutionA particle is revolving in a circular path of radius 2 m with constant angular speed 4 rad/s. The angular acceleration of particle is
View SolutionA particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle moves in a circle of radius 4 m with a linear velocity of 20ms−1. Find the angular velocity.
View SolutionStarting from rest, a particle rotates in a circle of radius R = √2m with an angular acceleration = π4 rad/s2.The magnitude of average velocity of the particle over the time it rotates quarter circle is:
View Solution
