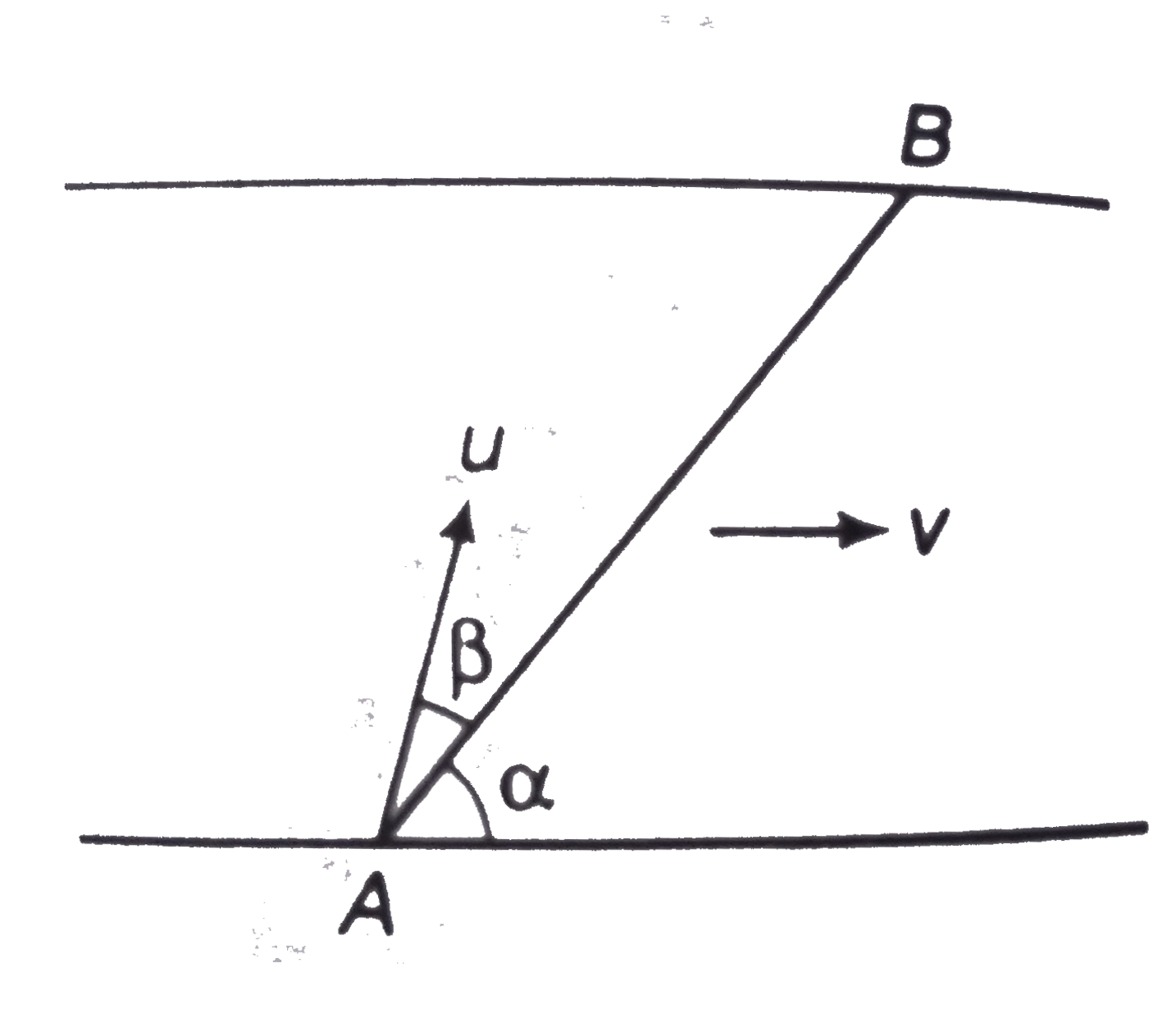
A launch plies between two points A and B on the opposite banks of a river always following the line AB. The distance S between points and B is 1200 m. The velocity of the river current v=1.9m/s is constant over the entire width of the river. The line AB makes an angle α=60∘ with the direction of the current. With what velocity u and at what angle beta to the line AB should the launch move to cover the distance AB and back in a time t=5min? The angle beta remains the same during the passage from A to B and from B to A.
The correct Answer is:tan−1√317;√85ms−1
From A to B : AB=(vcosβ+ucos∝)t1
From B to A : AB=(ucosβ−ucos∝)t2
∝=60∘,vsinβ=usin∝...(i)
⇒5×60=1200vcosβ+ucos∝+1200(vcosβ−vcos∝)
Putting u=√17,∝=60∘, we get
v2cos2β−8vcosβ−174=0⇒vcosβ=172 ...(ii)
From Eqs. (i) and (ii), tanβ=√317
⇒β=tan−1√317andv=(√85)ms−1.

Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A man wants to swim in a river from A→B and back from B→A always following line AB (Fig. 5.94). The distance between points AandB is S. The velocity of the river current v is constant over the entire width of the river. The line AB makes an angle ∝ with the direction of current. The man moves with velocity u at angle β to the line AB. The man swim to cover distance AB and back, find the time taken to complete the journey.
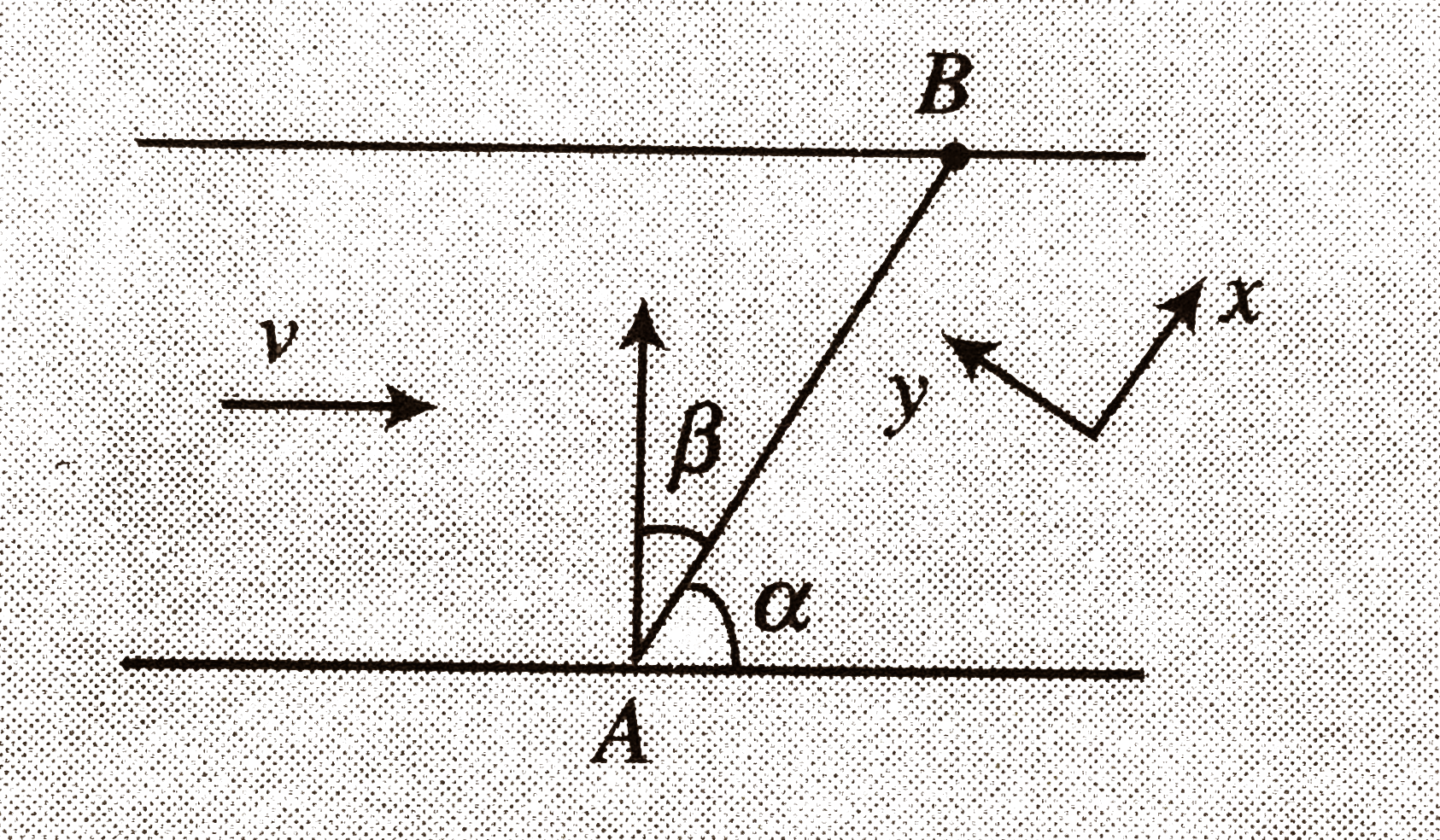 .
.
View SolutionTwo trees, A and B are on the same side of a river. From a point C in the river the distance of trees A and B are 25 m and 300 m respectively. If the angle C is 450 , find the distance between the trees (use √2=1.44)
View Solution
Knowledge Check
The distance between two points differing in phase by 60∘ on a wave, velocity 360 m./s and frequency 500 Hz is
A24 cmB12 cmC6 cmD1 cm
A swimmer wishes to reach directly opposite bank of a river, flowing with velocity 8 m/s. The swimmer can swim 10 m/s still water. The width of the river is 480 m. Time taken by him to do so:
View SolutionA person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
View SolutionA person standing on the bank of a river observes that the angle subtended by a tree on the opposite of bank is 60∘. When he retires 40 m.from the bank, he finds the angle to be 30∘. What is the breadth of the river ?
View SolutionA boat moves perpendicular to the bank with a velocity of 7.2 km/h. The current carries it 150 m downstream, find the velocity of the current. (The width of the river is 0.5 km).
View SolutionVelocity of the boat with respect to river is 10 m/s. From point A it is steered in the direction shown to reach point C. Find the time of the trip and distance between B and C

View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View Solution
