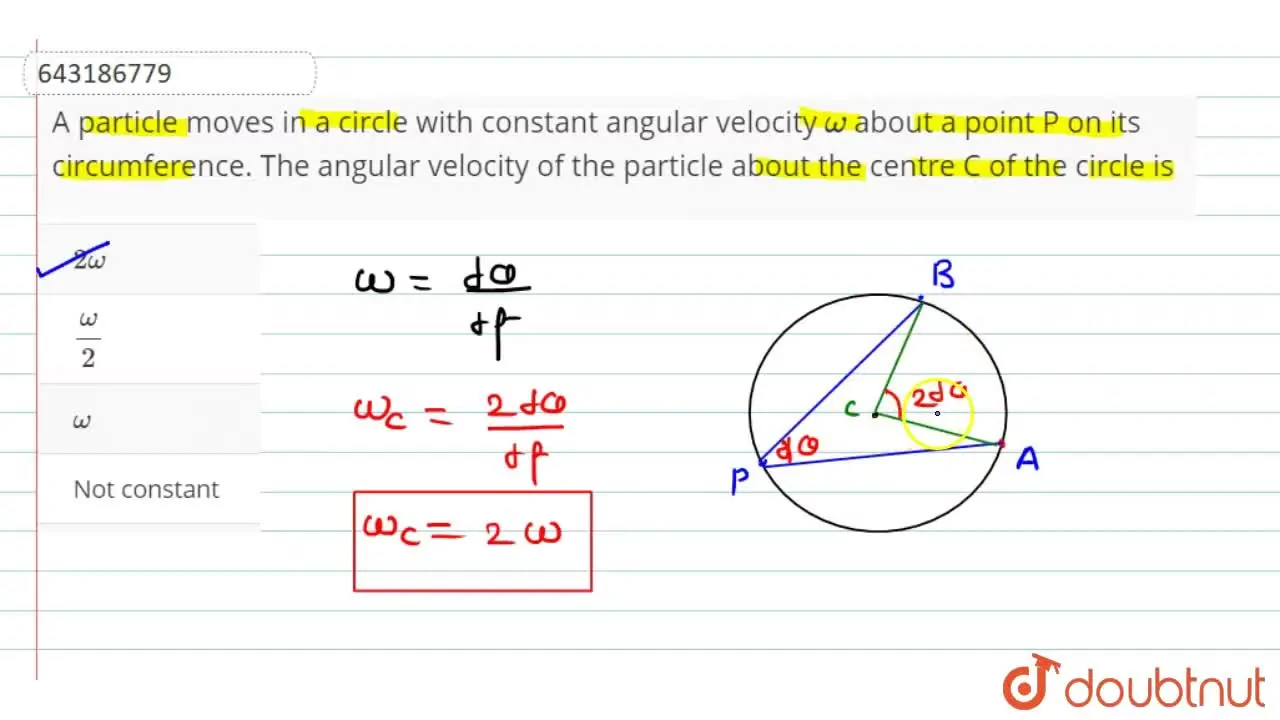
A particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
2ω
ω2
ω
Not constant
The correct Answer is:A
Step by step video & image solution for A particle moves in a circle with constant angular velocity omega about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct86videos
ROTATIONAL MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct36videos
ROTATIONAL MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
Similar Questions
A particle moves with constant angular velocity in a circle. During the motion its
View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O

View SolutionA particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
View SolutionConsider a particle , moving in a circle with constant speed . P is a point outside the circle , in the same plane . Then , the angular momentum of the particle about the point P is
 View Solution
View SolutionA particle moves in a circle of radius r with angular velocity ω. At some instant its velocity is v radius vector with respect to centre of the circle is r. At this particular instant centripetal acceleration ac of the particle would be
View SolutionA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
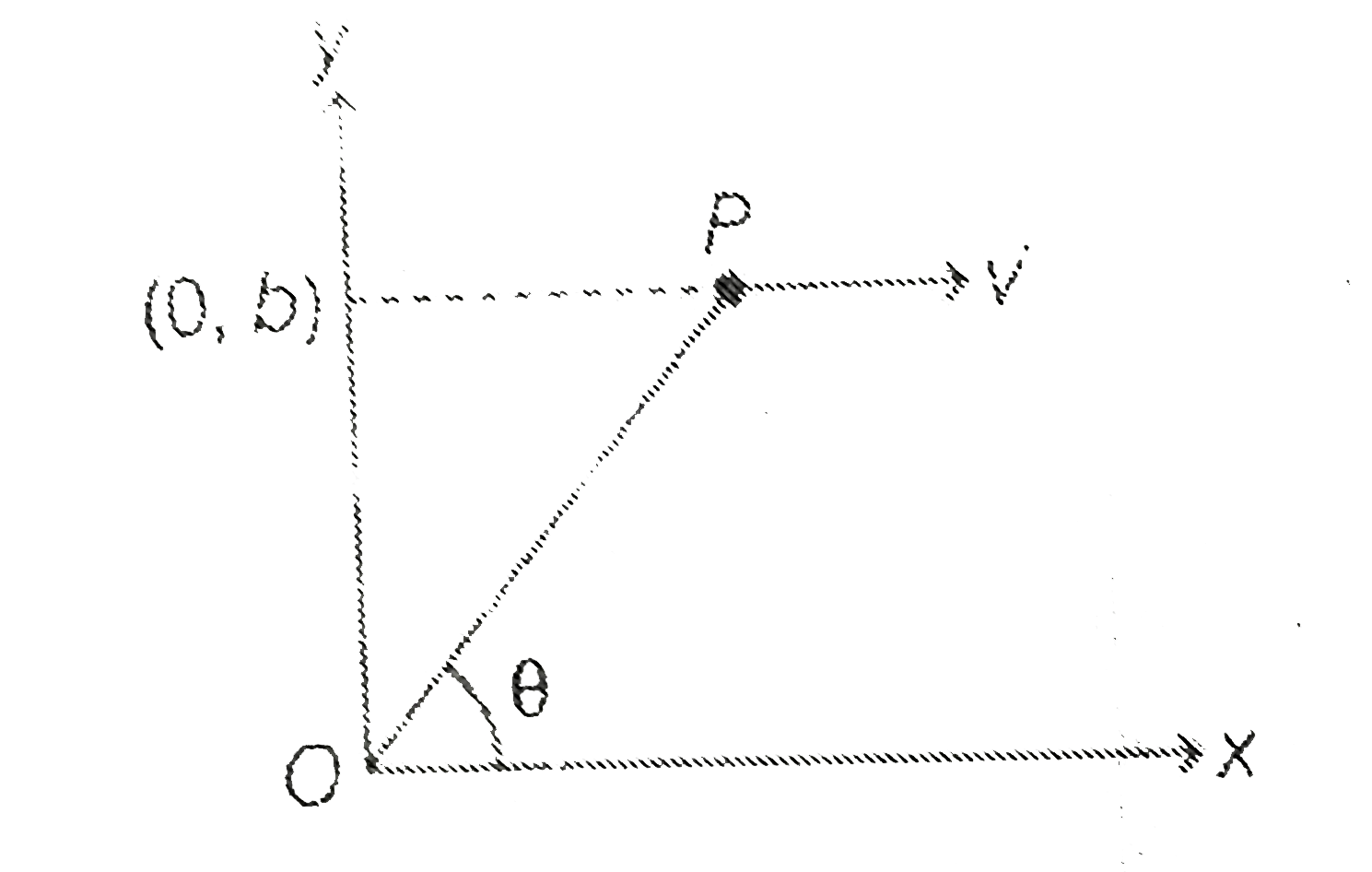 View Solution
View SolutionIf a point moves along a circle with constant speed, prove that its angular speed about any point on the circle is half of that about the centre.
View SolutionA particle moves in a circular path with constant speed .Find out a point about which the angular momentum of the particle is constant and another point about which changes with time.
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 View Solution
View SolutionA particle moves on a straight line with a uniform velocity. It's angular momentum
View Solution