A particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
The correct Answer is:C, D
To solve the problem step by step, we will analyze the motion of the particle projected from the bottom of an inclined plane.
Step 1: Understand the Problem
We have a particle projected with an initial velocity of u=40m/s at an angle of 60∘ with respect to the horizontal from the bottom of an inclined plane that has an inclination of 30∘. We need to find the speed of the particle when its velocity vector is parallel to the inclined plane.
Step 2: Draw the Diagram
Draw a diagram of the inclined plane. Mark the angle of inclination θ=30∘ and the angle of projection ϕ=60∘.
Step 3: Resolve the Initial Velocity
We need to resolve the initial velocity u into its horizontal and vertical components:
- The horizontal component ux:
ux=ucos(60∘)=40cos(60∘)=40×12=20m/s
- The vertical component uy:
uy=usin(60∘)=40sin(60∘)=40×√32=20√3m/s
Step 4: Analyze the Motion When Velocity is Parallel to the Plane
When the velocity vector is parallel to the inclined plane, the angle between the velocity vector and the inclined plane is 0∘. Thus, the vertical component of the velocity must equal the horizontal component of the velocity when projected onto the inclined plane.
Let V be the speed of the particle when its velocity is parallel to the plane. The angle made by the velocity vector with the horizontal is 30∘ (the same as the inclination of the plane).
Step 5: Resolve the Final Velocity
The horizontal component of the final velocity Vx:
Vx=Vcos(30∘)=V×√32
The vertical component of the final velocity Vy:
Vy=Vsin(30∘)=V×12
Step 6: Set Up the Equation
Since there is no horizontal acceleration, the horizontal component of the initial velocity must equal the horizontal component of the final velocity:
ux=Vx
20=V×√32
Step 7: Solve for V
Rearranging the equation gives:
V=20×2√3=40√3m/s
Final Answer
Thus, the speed of the particle when its velocity vector is parallel to the inclined plane is:
V=40√3m/s≈23.09m/s
We have a particle projected with an initial velocity of u=40m/s at an angle of 60∘ with respect to the horizontal from the bottom of an inclined plane that has an inclination of 30∘. We need to find the speed of the particle when its velocity vector is parallel to the inclined plane.
Draw a diagram of the inclined plane. Mark the angle of inclination θ=30∘ and the angle of projection ϕ=60∘.
We need to resolve the initial velocity u into its horizontal and vertical components:
- The horizontal component ux:
ux=ucos(60∘)=40cos(60∘)=40×12=20m/s
uy=usin(60∘)=40sin(60∘)=40×√32=20√3m/s
When the velocity vector is parallel to the inclined plane, the angle between the velocity vector and the inclined plane is 0∘. Thus, the vertical component of the velocity must equal the horizontal component of the velocity when projected onto the inclined plane.
The horizontal component of the final velocity Vx:
Vx=Vcos(30∘)=V×√32
Vy=Vsin(30∘)=V×12
Since there is no horizontal acceleration, the horizontal component of the initial velocity must equal the horizontal component of the final velocity:
ux=Vx
20=V×√32
Rearranging the equation gives:
V=20×2√3=40√3m/s
Thus, the speed of the particle when its velocity vector is parallel to the inclined plane is:
V=40√3m/s≈23.09m/s
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Single Correct
10 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Single Correct
16 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α (from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
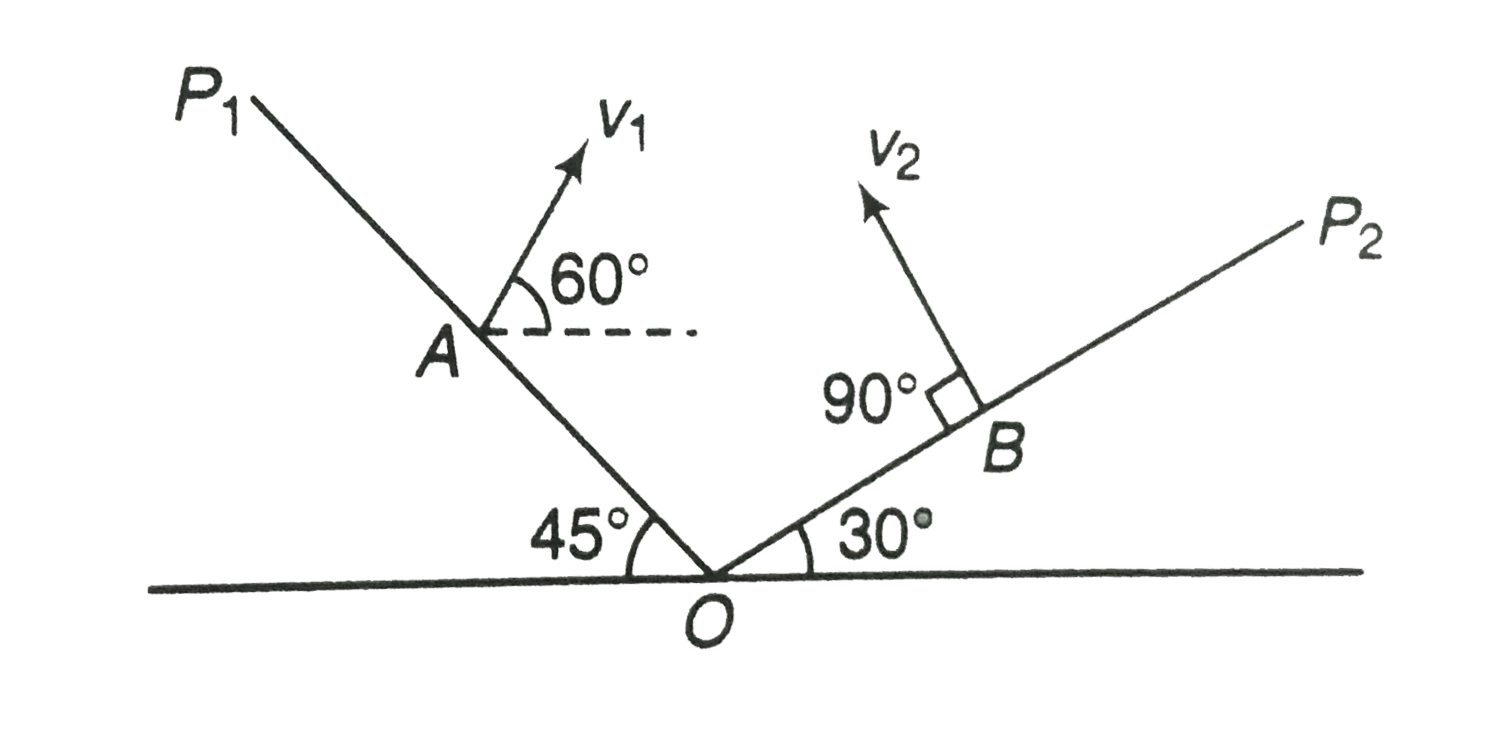
View SolutionA particle is projected from an inclined plane OP1 from A with velocity v1=8ms−1 at an angle 60∘ with horizontal. An another particle is projected at the same instant from B with velocity v2=16ms−1 and perpendicular to the plane OP2 as shown in figure. After time 10(√3) s there separation was minimum and found to be 70m. Then find distance AB.
View SolutionA particle is projected upwards with a velocity of 100m/s at an angle of 60∘ with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g=10m/s2.
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.

View SolutionA projectile is thrown with a velocity of 20 m/s, at an angle of 60∘ with the horizontal. After how much time the velocity vector will make an angle of 45∘ with the horizontal (in upward direction) is (take g=10m/s2)−
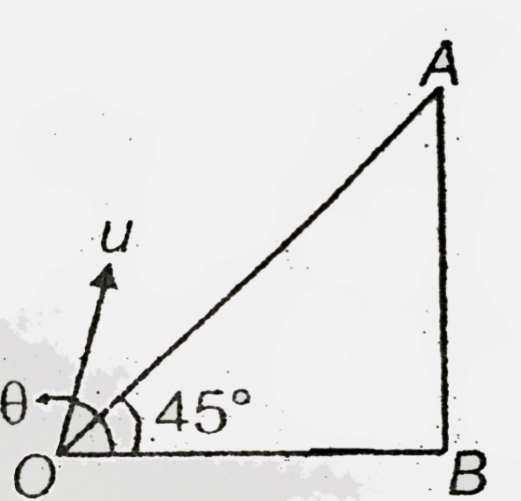
View SolutionA particles is projected from the foot of an inclined plane having inclination 45∘ , with the velocity u at angle θ(>45∘) with the horizontal in a vertical plane containing the line of greatest slope through the point of projection. Find the value of tanθ if the particle stikes the plane.
(i) Horizontally
(ii) Normally
View SolutionA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
View SolutionA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View Solution
