A ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall. Find the angle of projection of ball.
The correct Answer is:A, B, C
y=x(1−xR)tanα

∴tanα=yRx(R−x)
=(3)(24)(6)(18)=23
∴α=tan−1(23).
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Single Correct10videos
PROJECTILE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct8videos
PROJECTILE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Single Correct16videos
PROJECTILE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery32videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer8videos
PROPERTIES OF MATTER
Similar Questions
A ball is thrown from ground level so as to just clear a wall 4 m high at a distance of 4 m and fall at a distance of 14 m from the wall. Find the magnitude and direction of the velocity of the ball.
View SolutionA ball is thrown from the ground so that it just crosses a wall 5m high at a distance of 10m and falls at a distance of 10m ahead from the wall. Find the speed and the direction of projection of ball. Assume, g=10 ms–2
View SolutionA ball is projected from ground in such a way that after 10 seconds of projection it lands on ground 500 m away from the point of projection. Find out :-
(i) angle of projection
(ii) velocity of projection
(iii) Velocity of ball after 5 secondsView SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionA shell fired from the ground is just able to cross horizontally the top of a wall 90m away and 45m high. The direction of projection of the shell will be.
View SolutionA ball is thrown horizontally from the top of a lower of unkown height .Ball strikes a vertical wall whose plane is normal to the plane of month of ball Collison is elastic and ball falls on ground exactly at the midpoints between the lower and the wall ball strikes the grouind at an angle of the 30∘ with horizontal .Find the hieght of the tower (in meter)
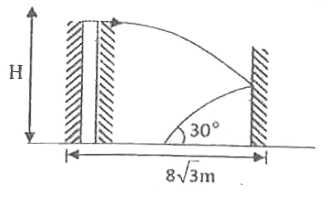 View Solution
View SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at some distance from the point of projection and returns on the same level. Coefficient of restitution between the ball and the wall is e, then time taken in path AB and maximum height attained by the ball is
 View Solution
View SolutionA ladder 3.7 m long is placed against a wall in such a way that the foot of the ladder is 1.2 m away from the wall. Find the height of the wall to which the ladder reaches.
View SolutionA ball is projected at t=0 with velocity v0 at angle θ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
View SolutionA ball is thrown vertically upwards with a velcotiy of 20ms−1 from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10ms−2.
View Solution


