Question

Derive an expression for the electric field at a point due to an infinitely long thin charged straight wire using Gauss Law.

Explanation

Statement : The total electric flux through a closed surface in free space is equal to `1/epsilon_0` times the net charge enclosed by the surface.
i.e., `phi=q/epsilon_0`

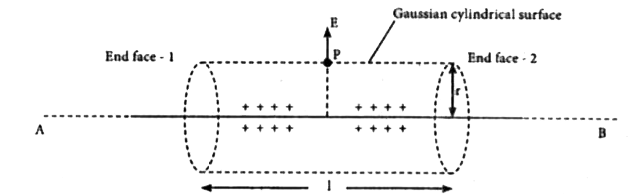
In the above fig.
AB is the infinitely long wire
E is the electric field
P is a point at a distance r from the wire
.r. is the radius of Gaussian cylinder
.l. is the length of the Gaussian cylinder
Let .q. be the charge enclosed by the Gaussian cylinder . Let `.lambda.` be the linear charge density on the wire .
Flux through the end faces is zero because there are no components of electric field along the normal to the end faces.
`phi`=flux through curved surface
`phi`=E x area of curved surface (`phi`=E x area)
`phi=E xx 2pirl to` (1)
From Gauss.s theorem
`phi=q/epsilon_0 to` (2)
But `lambda=q/l rArr q=lambdal`
(2)`rArr phi=(lambdal)/epsilon_0 to` (3)
On comparing (1) and (3) , we get
`Exx2pirl=(lambdal)/epsilon_0`
`E=lambda/(2piepsilon_0)`
`E=1/(2piepsilon_0) lambda/r`
The direction of .E. is perpendicular to the wire and directed away from the wire .