Using Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
Considering the whole line charge to be made of symmetrically situated length elements, each of length dI, it is clear from the figure shown that, the resultant field will be directed perpendicular to the line charge as shown-

To find magnitude
Now considering a cylindrical gaussian surface of radius r and length l , passing through point p , as shown
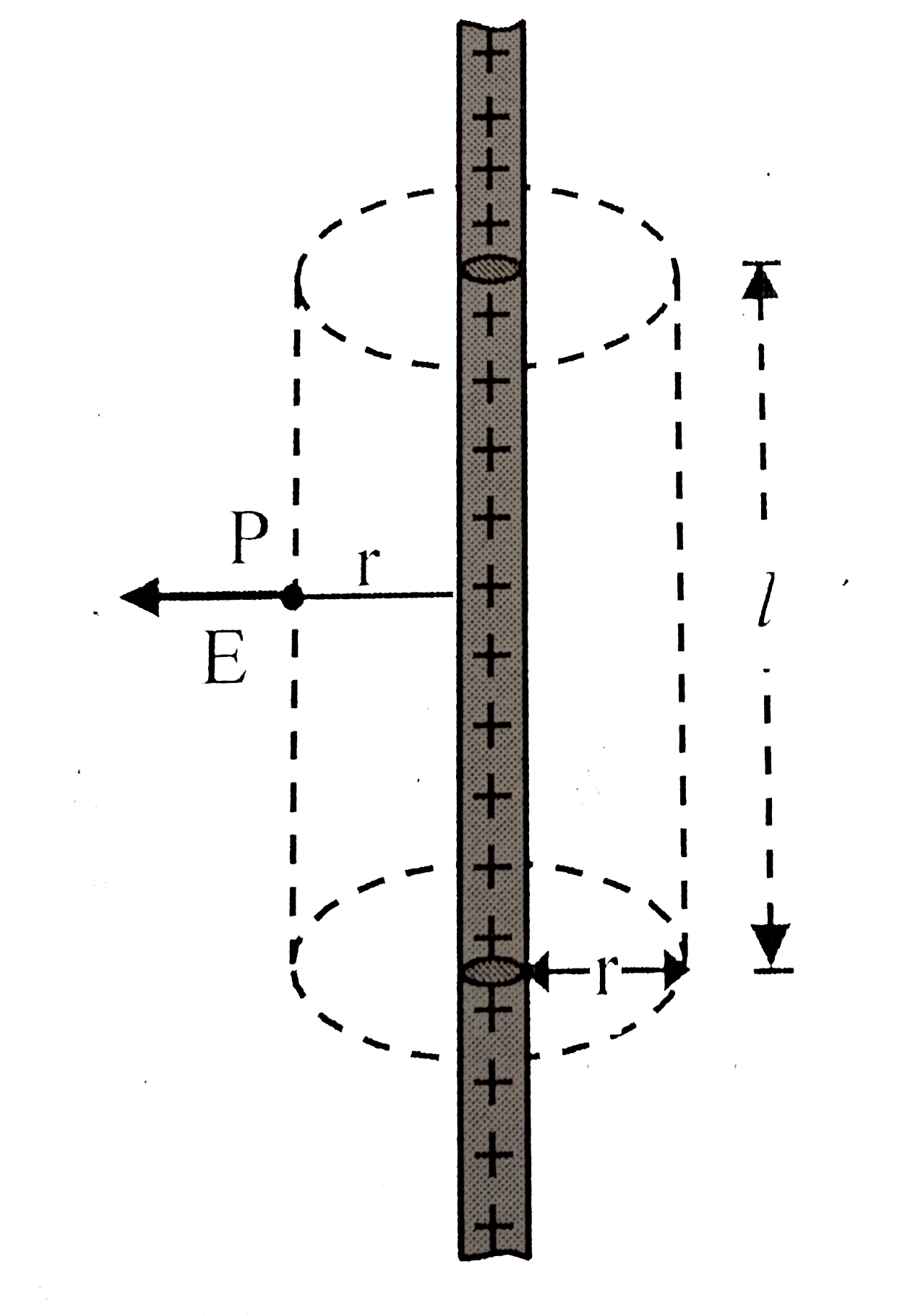
Flux through the Gaussian Surface= Flux through the curved Cylindrical part Φ=E×2πrl .....(1) , But according to Gauss’ law [Φ=Σqε0]
net electric flux emerging from cylindrical surface is [Φ=λlε0] ....(2) [ The surface includes charge equal to λl ]
Now , eliminatingΦ–– from equation (1) & (2), we get
E×2πrl=λε0 or E=λ2πε0r=2kλr
And in vector form →E=2kλr2→r
Topper's Solved these Questions
Similar Questions
Using Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
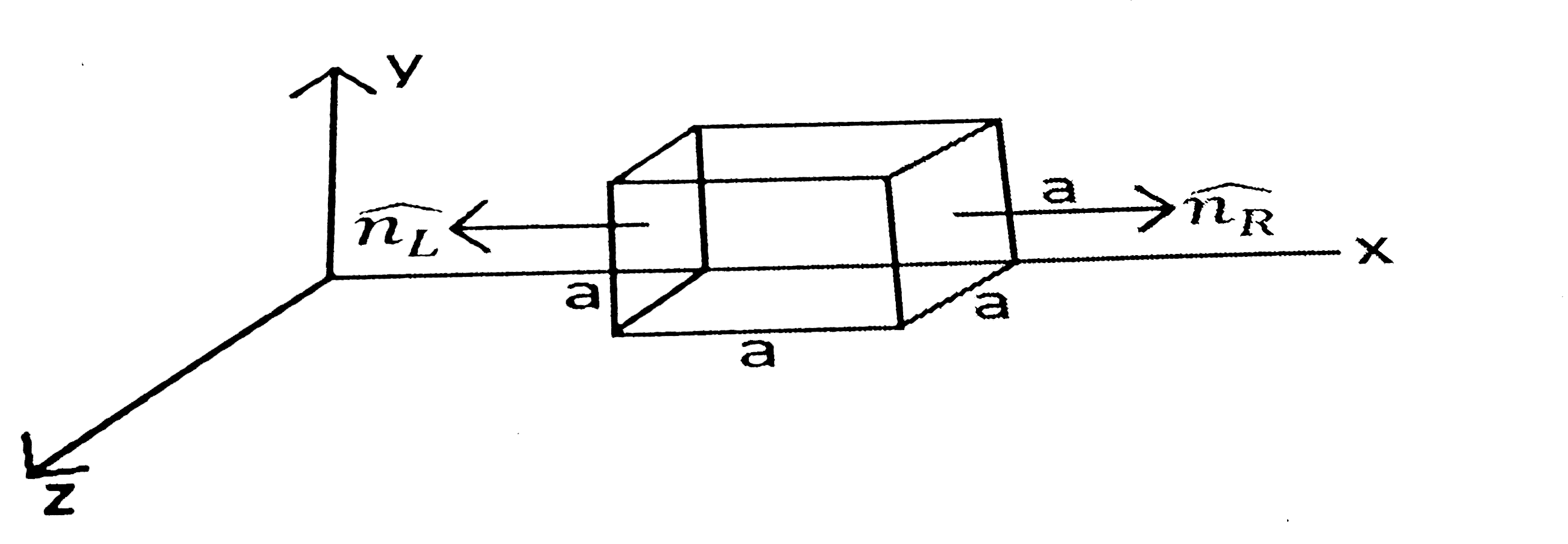
View Solution(a) Using Gauss's law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
(b) The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/Cm. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a=0.1m.
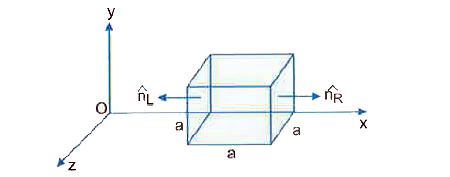
View SolutionUsing Gauss's law, derive an expression for the electric field intensity at any point near a uniformly charged thin wire of charge/length=λC/m.
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.
View SolutionState Gauss's law in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λcm−1
View SolutionUsing Gauss's law derive an expression for the electric field at any point outside a uniformaly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charges density of the sphere is (i) positive (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100μC/m2 Calculate the
(i) charge on the sphere (ii) total electric flux passing through the sphere.
View SolutionDerive an expression for the electric field intensity at a point outside an infinitely long charged cylindrical conductor.
View SolutionThe electric field at a point near an infinite thin sheet of a charged conductor is .
View SolutionState Gauss' law in electrostatic. Using it derive an expression for the electric field due to an infinitely long straight wire of linear charge density λ C/m.
View SolutionState Gauss's law on electrostatics and derive an expression for the electric field due to a long straight thin uniformly charged wire (linear charge density ) at a point lying at a distance r from the wire.
View Solution