(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density
σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.
(a) Electric field intensity at any point outside a uniformly charged spherical shell :
Consider a thin spherical shell of radius R with centre O. Let charge +q is uniformly distributed over the surface of the shell.
Let P be any point on the sphere S1 with centre O and radius r.
According to Gauss's law
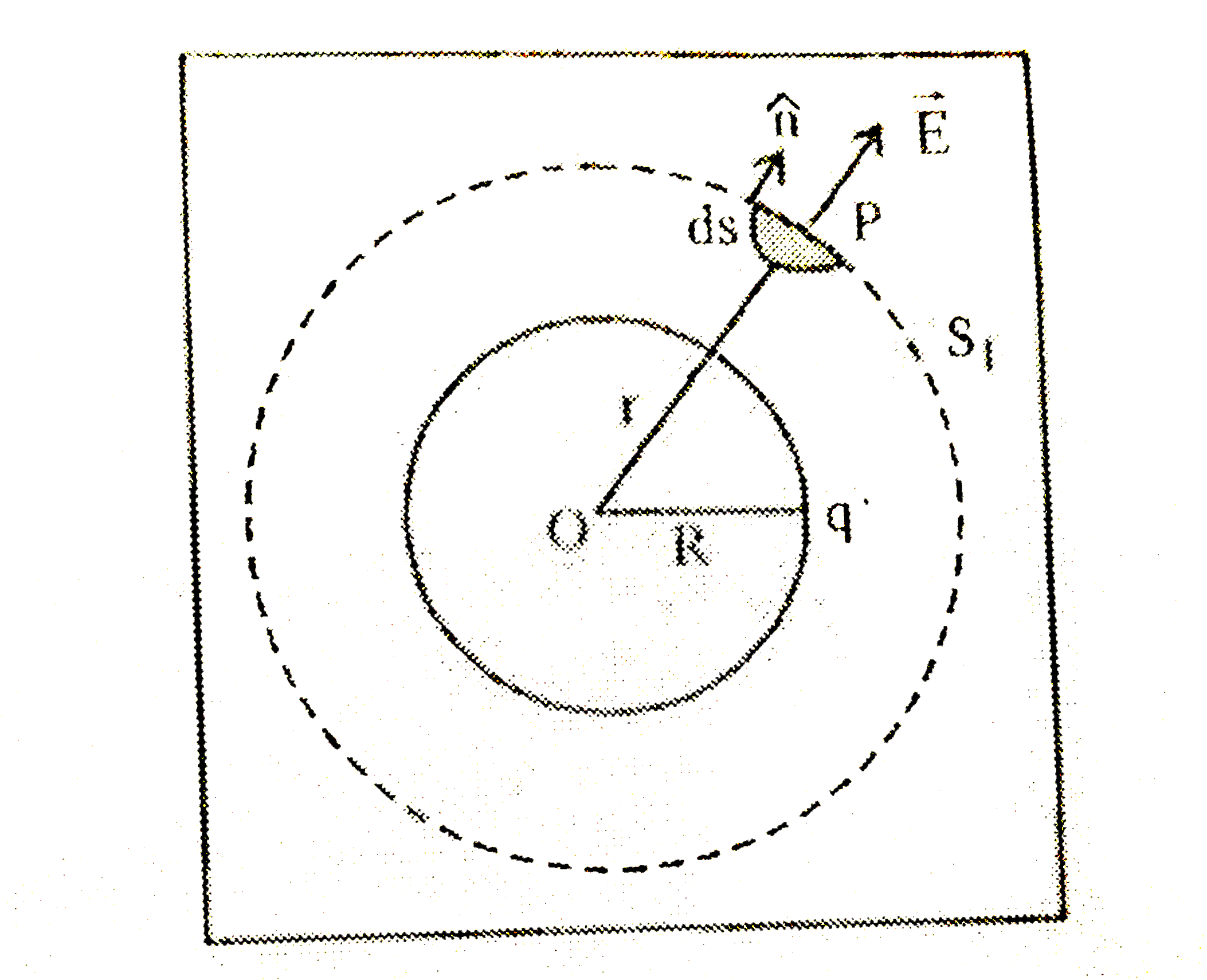
∮s→E.→ds=q∈0⇒∮E→E.→nds=q∈0
∴E∮ds=q∈0⇒E.4πr2=q∈0 ∴E=14π∈0.qr2
At any point on the surface of the shell, r=R
∴e=14π∈0.qR2
If σ is charge density ∴q=4πR2σ
∴E=14π∈0.4πR2σR2 Hence, E=σ∈0
Electric field lines when the charged density of the sphere:
(i) Positive (ii) Negative

(b) Here diameter = 2.5 m ∴2.52=1.25m.
Charge density σ=100μc/m2=100×10−6=10−4c/m2
(i)q=4πR2σ=4×3.14(1.25)2×10−4=19.625×10−4=1.96×10−3C.
(ii) Total electrifix ϕE=q∈0
∴ϕE=1.96×10−138.85×10−12=0.221×109=2.2×108Nm2/C.
Topper's Solved these Questions
Similar Questions
Using Gauss's law derive an expression for the electric field at any point outside a uniformaly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charges density of the sphere is (i) positive (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100μC/m2 Calculate the
(i) charge on the sphere (ii) total electric flux passing through the sphere.
View SolutionDerive an expression for the electric field intensity at a point outside a charged conducting sphere.
View Solution
Knowledge Check
A uniformly charged conducting sphere of 4.4 m diameter has a surface change density of 60μCm−2. The charge on the sphere is
A7.3×10−3CB3.7×10−6CC7.3×10−6CD3.7×10−3C
The expression for electric field intensity at a points outside uniformly charged thin plane sheet is (where, d is the distance of point from plane sheet)
View SolutionUsing Gauss's theorem derive an expression for the electric field at any point outside a charged spherical shell of radius R and of charge density σC/m2
View SolutionA uniformaly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0μC/m2
Find the charge on the sphere.
(b) What is the total electric flux leaving the surface of the sphere?
View SolutionA uniformly charged conducting sphere of 2.4m diameter has a surface density of 80.0μC/m2. (a) Find the charge on the sphere (b) What is the total electric flux leaving the surface of the sphere ?
View SolutionA uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 180.0μC/M2 (ii) Find the charge on the sphere. (ii) what is the total flux leaving the surface of the sphere ?
View SolutionUsing Gauss's law, derive an expression for the electric field intensity at any point near a uniformly charged thin wire of charge/length=λC/m.
View SolutionFind expression for electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell.
View Solution
