The expression for electric field intensity at a points outside uniformly charged thin plane sheet is (where, d is the distance of point from plane sheet)
Electric field intensity at a point outside uniformly charged thin plane sheet :
Consider an infinite thin plane sheet of positive charge having a unform surface charge density σ on both sides of the sheet. By symmetry, electric field perpendicular to plane sheet and directed outwards. Electric field intensity has same magnitude at a given distance on either sides of the sheet.
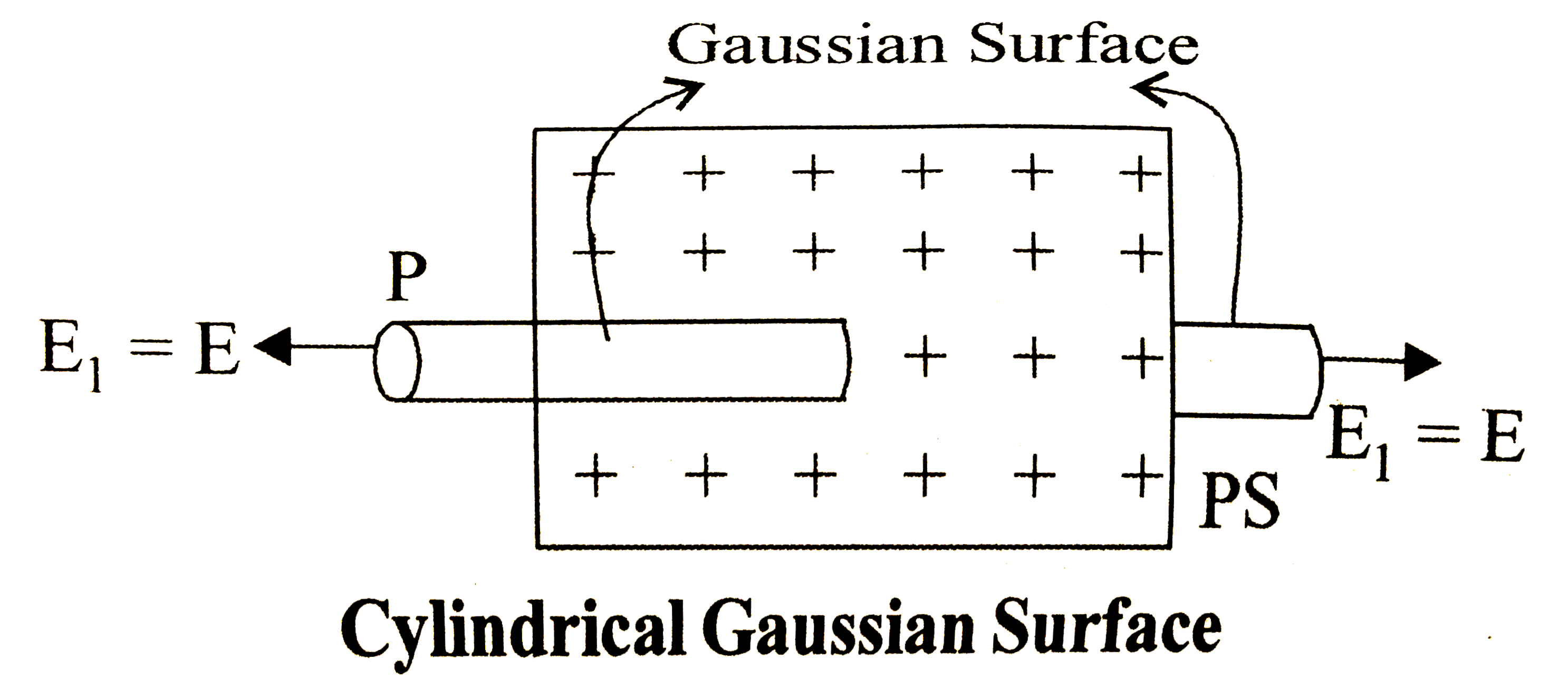
Let P be the point at which electric field intensity is to be found, E be electric field intensity at point P, S be Gaussian surface and PS is plane sheet.
To find electric field intensity at a point P due to uniformly charged infinite thin plane sheet, an imaginary cylinder is constructed around P with its axis perpendicular to plane sheet carrying charge with ends having cross-sectional area ds. The plane sheet passes through the middle of cylinder's length in such a way that the ends of cylinder are equidistant from the plnae sheet carrying charge.
Electric field intensity (→E) is perpendicular to the ends of cylinder, hence the electric flux througth each end is Eds. Since →E is perpendicular to the plane sheet, it is parallel to the curved surface of Gaussian cylinder.
∴ Electric flux passing througth curved surface =0
Total normal electric induction over Gaussian surface = εE(2ds)
Where, ds is surface area of end faces of cylinder.
Algebraic sum of charges enclosed by Gaussian cylinder =σds
As per Gauss' law,
εE(2ds)=σds
∴E=σ2ε
This is the expression of electric field intensity at a point outside uniformly charged thin plane sheet.
Similar Questions
The expression for electric field intensity at a points outside uniformly charged thin plane sheet is (where, d is the distance of point from plane sheet)
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionDerive an expression for the electric field intensity at a point outside a charged conducting sphere.
View SolutionFind expression for electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell.
View SolutionDerive an expression for the electric field intensity at a point outside an infinitely long charged cylindrical conductor.
View SolutionState Gauss's theoram in electric field at a point due to a uniformaly charged infinite plane thin sheet.
View SolutionDerive an expression for electric intensity E due to a uniformly charged thin spherical shell at a point outside the shell.
View SolutionDerive an expression for electric field intensity E due to an infinite place sheet of charge.
View SolutionUsing Gauss's law, derive an expression for the electric field intensity at any point near a uniformly charged thin wire of charge/length=λC/m.
View SolutionUsing Gauss' law porve that the electric field at a point due to a uniformaly charged infinite plane sheet is independent of the distance form it. How is the field directed if the sheet is
(i) positively charged, (ii) negatively charged.
View Solution

