Derive an expression for electric field intensity E due to an infinite place sheet of charge.
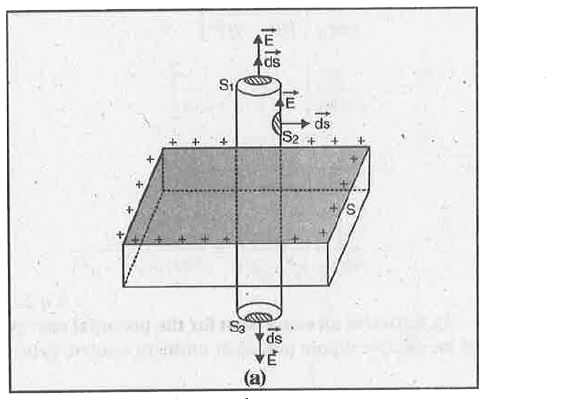
Consider a non-conducting infinite thin sheet of area S having surface area charge density σ. Let P be a point at certain distance where electric field →E is to be determined.
Consider a Gaussian surface passing through point P which is a cylinder passing through the sheet. let us divide this cylinder in three sections S1,S2andS3. consider an element of area dS in each section as shown in fig. (a).
According to Gauss.s theorem
∮S→E⋅d→S=qε0=σSε0
or ∮S1→E⋅d→S+∮S3→E⋅d→S+∮S2→E⋅d→S=σSε0
or ∫EdScos0∘+sinEdScos0∘+∫EdScos90∘=σSε0
or ∫EdS+∫EdS+0=σSε0
or 2∫EdS=σSε0
or 2E∫dS=σSε0
or 2ES=σSε0
or E=σ2ε0
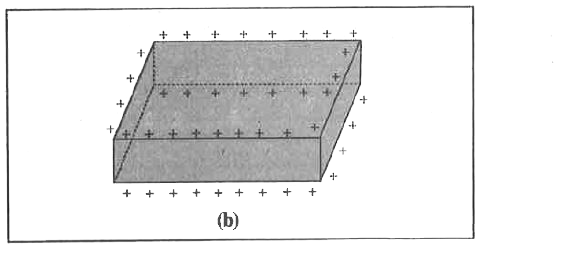
Note: For Conducting Sheet
If we have a conducting thin sheet, the charge will be distributed on both the upper and lower surface Fig (b).
Therefore, total charge enclosed by the cylindrical gaussian surface will be σ(2S). hence, as explained earlier we will have E=σ/ε0. that is the electric field due to an infinite conducting sheet is twice that due to a non-conducting sheet.
Related Playlists
- BOOK - MBD -HARYANA BOARDCHAPTER - ELECTROSTATICSEXERCISE - LONG ANSWER TYPE QUESTIONS14videos
ELECTROSTATICS
- BOOK - MBD -HARYANA BOARDCHAPTER - ELECTROSTATICSEXERCISE - OBJECTIVE TYPE QUESTIONS23videos
ELECTROSTATICS
- BOOK - MBD -HARYANA BOARDCHAPTER - ELECTROSTATICSEXERCISE - OBJECTIVE TYPE QUESTIONS23videos
ELECTROSTATICS
- BOOK - MBD -HARYANA BOARDCHAPTER - Electromagnetic WavesEXERCISE - Example7videos
Electromagnetic Waves
- BOOK - MBD -HARYANA BOARDCHAPTER - MAGNETISMEXERCISE - OBJECTIVE TYPE QUESTIONS17videos
MAGNETISM
Similar Questions
Derive an expression for electric field intensity at a point due to point charge.
View SolutionDerive an expression for the electric field intensity at a point outside an infinitely long charged cylindrical conductor.
View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
View SolutionState Gauss' law in electrostatic. Using it derive an expression for the electric field due to an infinitely long straight wire of linear charge density λ C/m.
View SolutionState Gauss's theorem in electrostatiics. State the expression for electric field intensity at a point outside an infinitely long charged conducting cylinder.
View SolutionApply Gauss's theorem to find an expression for the electric field intensity at a point due to a point charge.
View SolutionUsing Gauss's law, derive an expression for the electric field intensity at any point near a uniformly charged thin wire of charge/length=λC/m.
View SolutionState Gauss's law in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λcm−1
View SolutionDerive an expression for the electric field intensity at a point outside a charged conducting sphere.
View SolutionDerive an expression for electric intensity E due to a uniformly charged thin spherical shell at a point outside the shell.
View Solution


