Assertion : Bob is released from rest position A. Given θ0 very small. Angular velocity of bob about point O is maximum and (√gl)θ0 at point O.
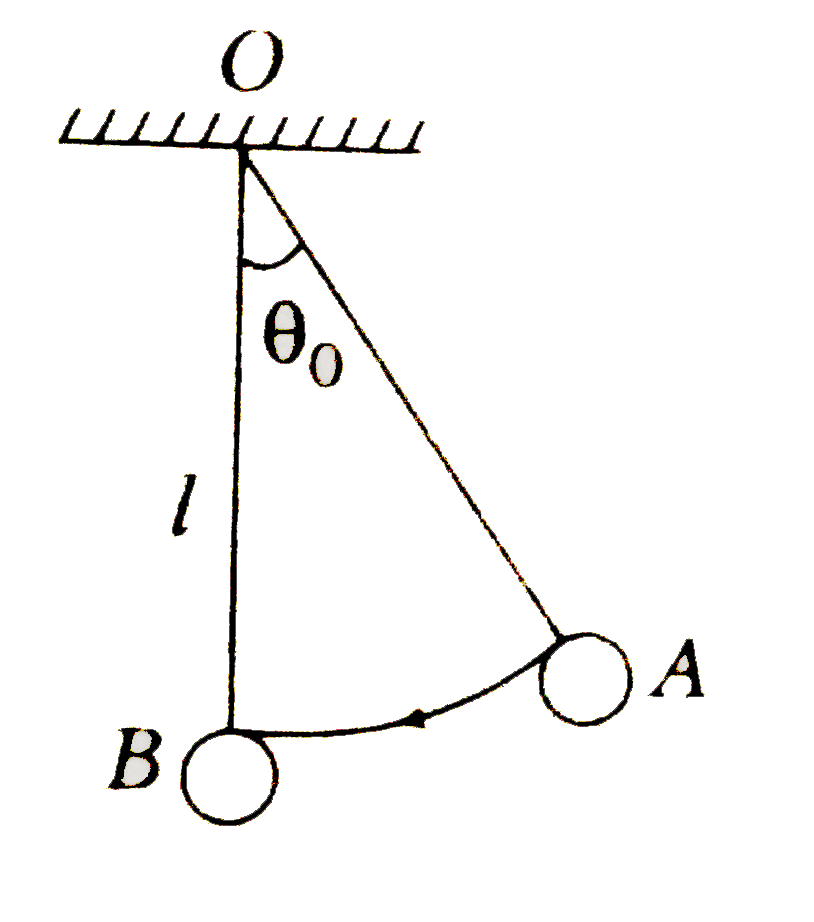
Reason : For small angular amplitudes , motion of bob is simple harmonic
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:B
(b) Maximum angular velocity =ωθ0
=(2πf)θ0=(2π)(12π√gl)θ0
=(√gl)θ0
Similar Questions
A simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.
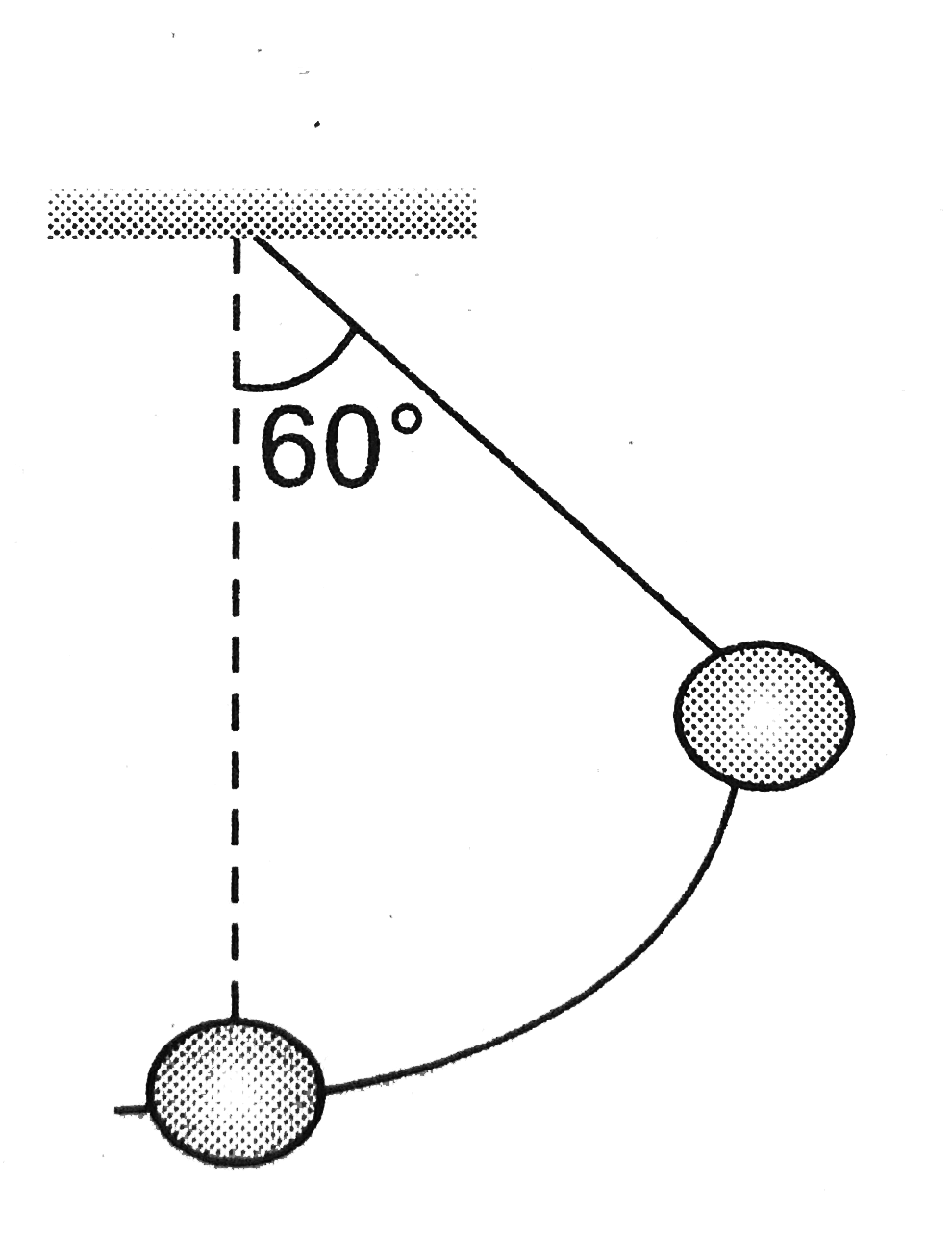
View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.

View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionAssertion: A particle is rorating in a circle with constant speed as shown. Between point A and B , ratio of average acceleration and average velocity is angular velocity of particle about point O .
Reason: Since speed is constant, angular velocity is also constant.
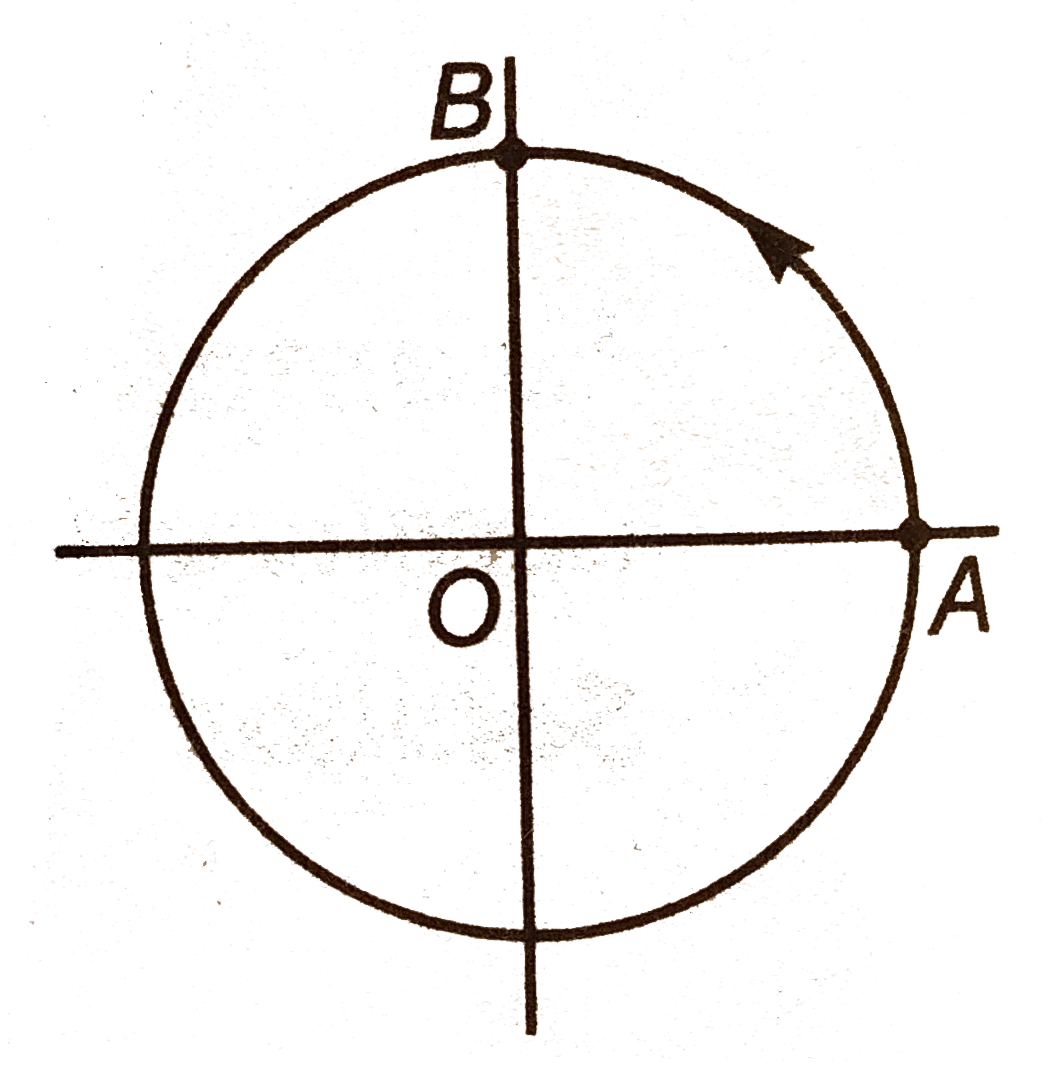
View SolutionThere are two pendulums with bobs having indencital size and mass. The pendulum A is released from rest in the position as shown in the figure. If the maximum angle formed by cord BO' with vertical in the subsequent motion of sphere B is equal to the angle θ0 If the coefficient of restitution between sphere A and sphere B is l. find

a. the velocities of sphere A and sphere B just after collisions
b. the ratio of lengths of pendulums lB/lA.
View SolutionA bob of mass m attached with a string of length l tied to a point on ceiling is released from a position when its string is horizontal. At the bottom most point of its motion, an identical mass m gently stuck to it. Find the maximum angle from the vertical to which it rotates.
View SolutionA simple pendulum of length l swimings from a small angle θ . Its swinging is constrained by the smooth inclined planes OP and PC. Assuming elastic collision of the bob with the plane PC, find
angular amplitude for the motion of the bob in the left hand side of its mean possition.
.

View SolutionA simple pendulum , made of a string of length l and a bob of mass m, is released from a small angle θ0 it strikes a block of mass M, kept on a horizontal surface at its lowest point of oscillations , elastically , it bounces back and goes up to an angle θ1 then M is given by :
View Solution
