The bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
x=θ0sin2π√(L/g)t
x=Lθ0cos2π√(g/L)t
x=Lθ0sin√(g/L)t
x=Lθ0cos√(g/L)t
The correct Answer is:D
As pendulum starts from EP
So equation of SHM is
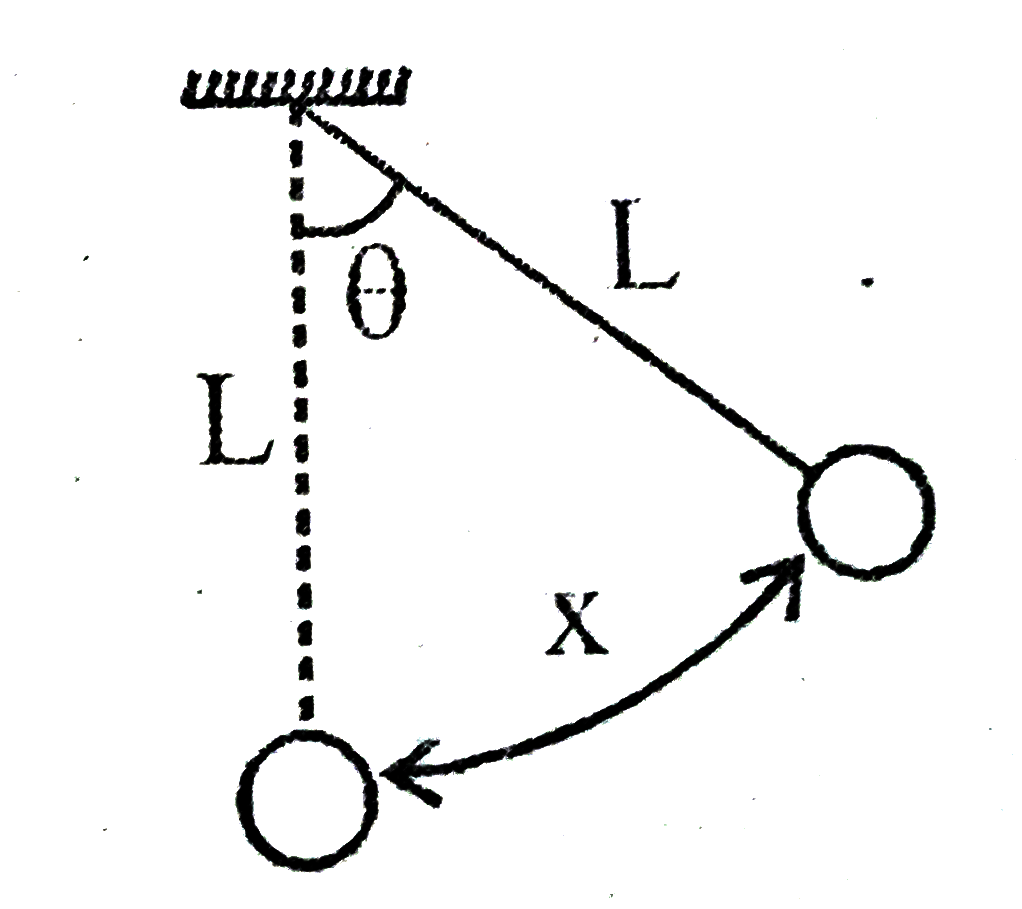
θ=θ0cosωt where ω=2πT
ω=2π2π√Lg=√gL
⇒θ=θ0cos√gLt
At time t
Linear displacement = x=Lθ
x=Lθ0cos√gLt
Topper's Solved these Questions
Similar Questions
The bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be its lowest position ?
View SolutionThe bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be at its lowest position?
View Solution
Knowledge Check
A simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
Amgl(1−cosθ)BmglcosθCmglsinθDNone of theseIf a simple pendulum of length l has maximum angular displacement θ, then the maximum velocity of the bob is
A√LgB2√glsin(θ2)C√2glsinθD√2glThe bob of simple pendulum having length 1, is displaced from mean position to an angular position o with respect to vertical. If it is released, then velocity of bob at equilibrium position is
A√2g(1−cosθ)B√2g(1+cosθ)C√2glcosθD√2gl
A simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
View SolutionA simple pendulum of mass 'm' , swings with maximum angular displacement of 60∘ . When its angular displacement is 30∘ ,the tension in the string is
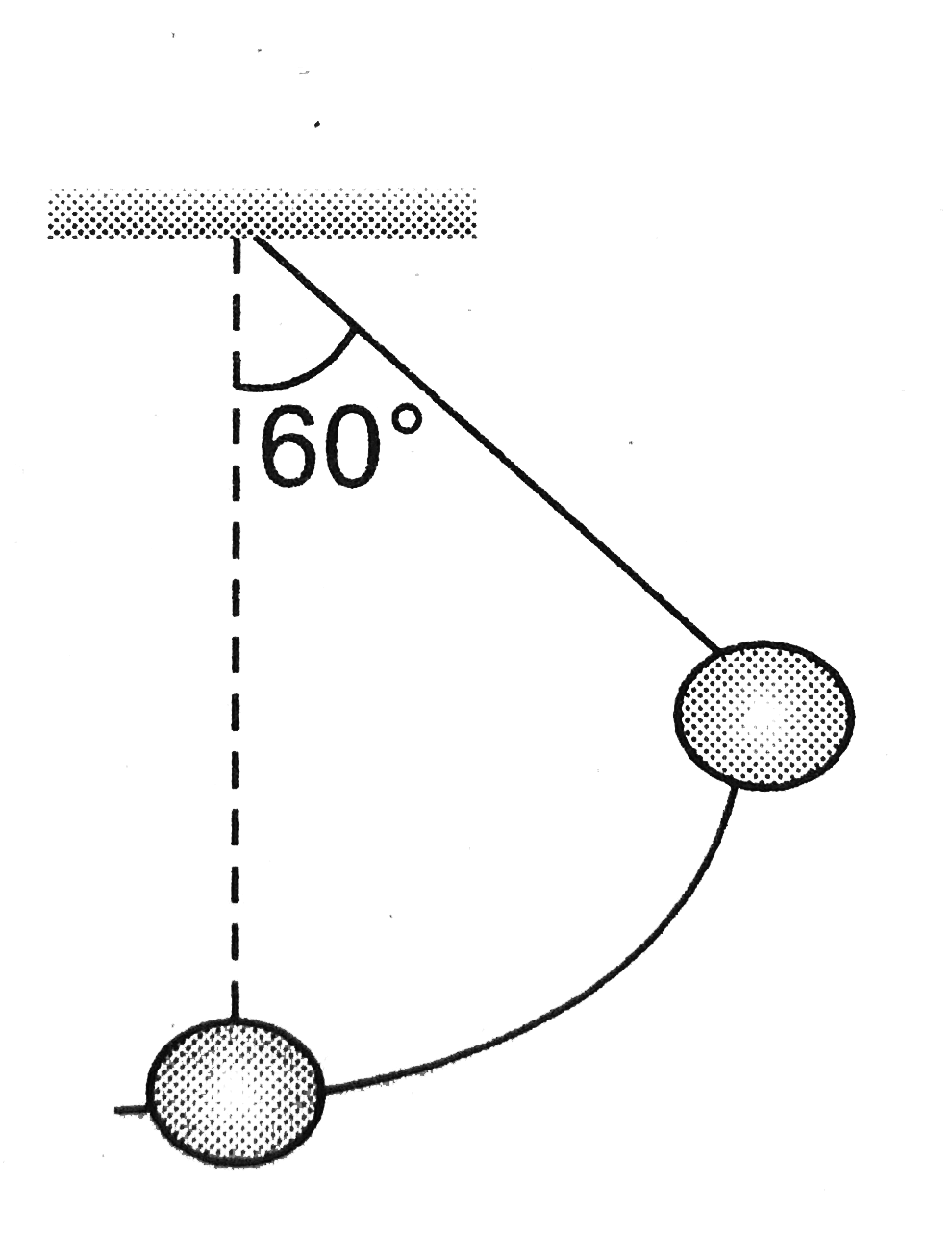
View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.
View SolutionThe metallic bob of a simple pendulum has the relative density ρ. The time period of this pendulum is T. If the metallic bob is immersed in water ,then the new time period is given by
View Solutiona simple pendulum with a bob of mass m savings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the strings is-
View Solution
