A simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
12mgl
12mglcosθ
mgl(1−cosθ)
12mglsinθ
The correct Answer is:C
To find the maximum kinetic energy of a bob of mass m in a simple pendulum of length l with a maximum angular displacement θ, we can follow these steps:
Step 1: Determine the height change
When the pendulum bob is at its maximum angular displacement (point A), it is at a height above its lowest point (point B). The height h that the bob descends when it swings down can be calculated as follows:
\(
h = l - l \cos \theta
\)
This simplifies to:
\(
h = l(1 - \cos \theta)
\)
Step 2: Use energy conservation to find maximum velocity
At the maximum height (point A), the bob has potential energy and no kinetic energy (since it is momentarily at rest). As it swings down to the lowest point (point B), all of the potential energy converts into kinetic energy.
Using the conservation of mechanical energy:
\(
\text{Potential Energy at A} = \text{Kinetic Energy at B}
\)
The potential energy at point A is given by:
\(
PE = mgh = mg \cdot h = mg \cdot l(1 - \cos \theta)
\)
At point B, the kinetic energy (KE) is given by:
\(
KE = \frac{1}{2} mv^2
\)
Setting the potential energy equal to the kinetic energy:
\(
mg \cdot l(1 - \cos \theta) = \frac{1}{2} mv^2
\)
Step 3: Solve for maximum velocity
We can cancel m from both sides (assuming m is not zero):
\(
g \cdot l(1 - \cos \theta) = \frac{1}{2} v^2
\)
Multiplying both sides by 2:
\(
2g \cdot l(1 - \cos \theta) = v^2
\)
Taking the square root gives us the maximum velocity:
\(
v = \sqrt{2g \cdot l(1 - \cos \theta)}
\)
Step 4: Calculate maximum kinetic energy
Now we can substitute v back into the kinetic energy formula:
\(
KE_{max} = \frac{1}{2} m v^2
\)
Substituting for v2:
\(
KE_{max} = \frac{1}{2} m (2g \cdot l(1 - \cos \theta))
\)
This simplifies to:
\(
KE_{max} = mg \cdot l(1 - \cos \theta)
\)
Conclusion
Thus, the maximum kinetic energy of the bob is:
\(
KE_{max} = mg \cdot l(1 - \cos \theta)
\)
When the pendulum bob is at its maximum angular displacement (point A), it is at a height above its lowest point (point B). The height h that the bob descends when it swings down can be calculated as follows:
h = l - l \cos \theta
\)
h = l(1 - \cos \theta)
\)
At the maximum height (point A), the bob has potential energy and no kinetic energy (since it is momentarily at rest). As it swings down to the lowest point (point B), all of the potential energy converts into kinetic energy.
\text{Potential Energy at A} = \text{Kinetic Energy at B}
\)
PE = mgh = mg \cdot h = mg \cdot l(1 - \cos \theta)
\)
KE = \frac{1}{2} mv^2
\)
mg \cdot l(1 - \cos \theta) = \frac{1}{2} mv^2
\)
We can cancel m from both sides (assuming m is not zero):
g \cdot l(1 - \cos \theta) = \frac{1}{2} v^2
\)
2g \cdot l(1 - \cos \theta) = v^2
\)
v = \sqrt{2g \cdot l(1 - \cos \theta)}
\)
Now we can substitute v back into the kinetic energy formula:
KE_{max} = \frac{1}{2} m v^2
\)
KE_{max} = \frac{1}{2} m (2g \cdot l(1 - \cos \theta))
\)
KE_{max} = mg \cdot l(1 - \cos \theta)
\)
Thus, the maximum kinetic energy of the bob is:
KE_{max} = mg \cdot l(1 - \cos \theta)
\)
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Level 1 Subjective
Explore 13 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Level 2 Single Correct
Explore 18 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Assertion And Reason
Explore 28 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEYChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
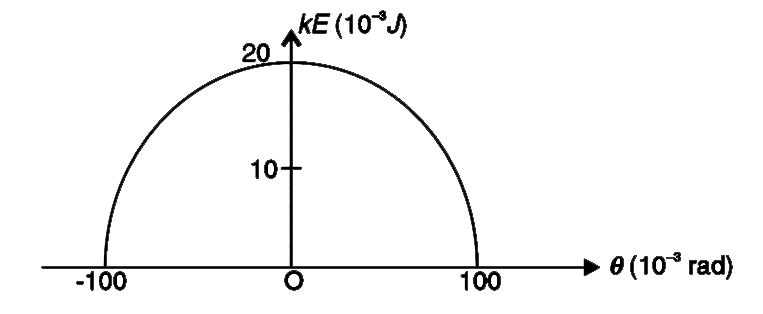
The given figure shows the variation of the kinetic energy of a simple pendulum with its angular displacement (θ) from the vertical. Mass of the pendulum bob is m = 0.2 kg. Find the time period of the pendulum. Take g=10ms−2.
View SolutionA string of length l and mass m is fixed at both ends with tension t and excited in its fundamental mode.The maximum displacement at the mid point is A Find (a) the maximum kinetic energy of the string ,9b0 the mean kinetic energy of the srting averaged over one oscillation period
hint Take sine distribution of amplitudes
View Solution
Knowledge Check
A simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
Amgl(1−cosθ)BmglcosθCmglsinθDNone of theseIf a simple pendulum of length l has maximum angular displacement θ, then the maximum velocity of the bob is
A√LgB2√glsin(θ2)C√2glsinθD√2glA simple pendulum is oscillating with a maximum angular displacement of θ radian. If θ is very small, the ratio of maximum tension to the minimum tension in the string during oscillations is
A(1+θ2):(1−θ2)B(1+θ2):(1−θ22)C(1+θ2):1D(1+θ22):(1−θ2)
A simple pendulum having a bob of mass 100 g is oscillating with a maximum angular displacement of 3∘. The maximum restoring force acting on the bob is (take g=10ms−2)
View SolutionA simple pendulum of mass 'm' , swings with maximum angular displacement of 60∘ . When its angular displacement is 30∘ ,the tension in the string is
View SolutionKinetic energy of the bob of a simple pendulum is maximum
View SolutionThe bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
View SolutionA simple pendulum oscillates with maximum displacement θ0 The time taken, when pendulum displaces from 0 to θ02 is t1 and time taken when pendulum displaces from θ02 to θ0 is t2 then what is true ?
View Solution

