Kinetic energy of the bob of a simple pendulum is maximum
at the mean position
at the extreme left position
at the extreme right position
none of these
The correct Answer is:A
To determine when the kinetic energy of the bob of a simple pendulum is maximum, we can analyze the motion of the pendulum step by step.
1. Understanding the Pendulum's Motion:
- A simple pendulum consists of a mass (bob) attached to a string that swings back and forth. The pendulum oscillates around a central point known as the mean position.
2. Identifying Key Positions:
- Mean Position: This is the lowest point in the swing where the bob hangs vertically down. Here, the forces acting on the bob are balanced (tension equals weight).
- Extreme Positions: These are the highest points on either side of the mean position, where the bob momentarily comes to rest before reversing direction.
3. Velocity at Different Positions:
- At the mean position, the bob is moving at its maximum speed because all the potential energy has been converted into kinetic energy.
- At the extreme positions (both left and right), the velocity of the bob is zero because it momentarily stops before changing direction.
4. Kinetic Energy Calculation:
- Kinetic energy (KE) is given by the formula:
KE=12mv2
where m is the mass of the bob and v is its velocity.
- Since the velocity at the extreme positions is zero, the kinetic energy at these points is:
KE=12m(0)2=0
- At the mean position, since the velocity is maximum, the kinetic energy is at its highest value.
5. Conclusion:
- Therefore, the kinetic energy of the bob of a simple pendulum is maximum at the mean position.
Final Answer:
The kinetic energy of the bob of a simple pendulum is maximum at the mean position.
---
- A simple pendulum consists of a mass (bob) attached to a string that swings back and forth. The pendulum oscillates around a central point known as the mean position.
- Mean Position: This is the lowest point in the swing where the bob hangs vertically down. Here, the forces acting on the bob are balanced (tension equals weight).
- Extreme Positions: These are the highest points on either side of the mean position, where the bob momentarily comes to rest before reversing direction.
- At the mean position, the bob is moving at its maximum speed because all the potential energy has been converted into kinetic energy.
- At the extreme positions (both left and right), the velocity of the bob is zero because it momentarily stops before changing direction.
- Kinetic energy (KE) is given by the formula:
KE=12mv2
where m is the mass of the bob and v is its velocity.
- Since the velocity at the extreme positions is zero, the kinetic energy at these points is:
KE=12m(0)2=0
- At the mean position, since the velocity is maximum, the kinetic energy is at its highest value.
- Therefore, the kinetic energy of the bob of a simple pendulum is maximum at the mean position.
The kinetic energy of the bob of a simple pendulum is maximum at the mean position.
Topper's Solved these Questions
- WAVE MOTION AND SOUND BOOK - MCGROW HILL PUBLICATIONCHAPTER - WAVE MOTION AND SOUND EXERCISE - HIGH ORDER THINKING QUESTIONS
22 Videos
- SOURCES OF ENERGY BOOK - MCGROW HILL PUBLICATIONCHAPTER - SOURCES OF ENERGY EXERCISE - ELEMENTARY QUESTIONS
82 Videos
- WORK AND ENERGYBOOK - MCGROW HILL PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - HIGHER ORDER THINKING QUESTIONS
29 Videos
Similar Questions
Knowledge Check
The velocity of simple pendulum is maximum at
AExtremesBHalf displacementCMean positionDEvery whereThe tension in the string of a simple pendulum is maximum, when the bob of the pendulum
Ais at the extreme positionBmidway between the mean position and extreme positionCis at the mean positionDstarts oscillating with very large amplitudesPotential energy of the bob is maximum
Aat the mean positionBat the extreme positionsCbetween the mean position and extreme positionsDnone of these
Durinig the oscillation of the bob of a simple pendulum, what is the quantity that remains constant?
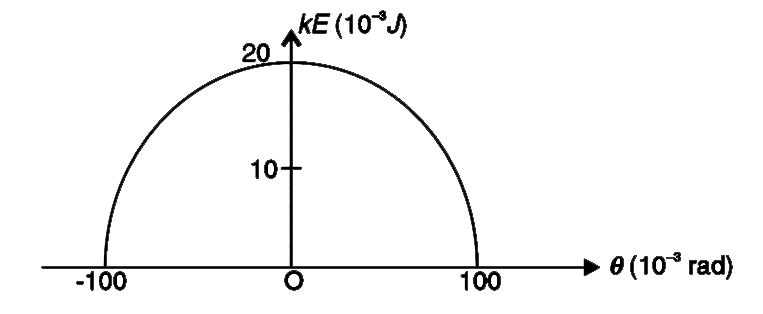
View SolutionThe given figure shows the variation of the kinetic energy of a simple pendulum with its angular displacement (θ) from the vertical. Mass of the pendulum bob is m = 0.2 kg. Find the time period of the pendulum. Take g=10ms−2.
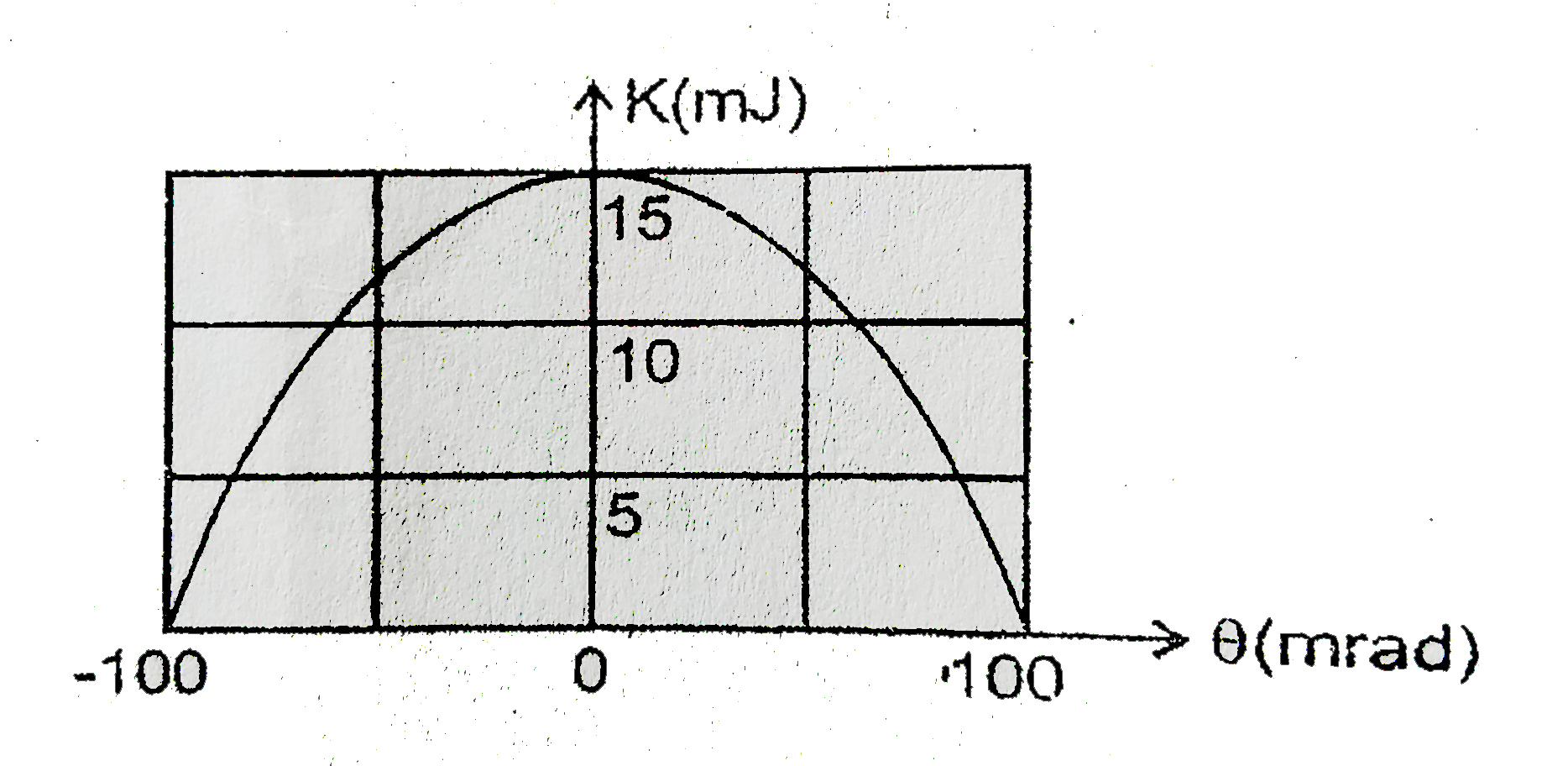
View SolutionFigure shows the kinetic energy K of a simple pendulum versus its angle θ from the verticle. The pendulum bob has mass 0.2kg. If the length of the pendulum is equal to ng meter. Then find n(g=10m/s2)
View SolutionIdentify wrong statements among the following
The greater the mass of a pendulum bob, the shorter is its frequency of oscillation
A simple pendulum with a bob of mass M swings with an angular amplitude of 40∘. When its angular amplitude is20∘, the tension in the string is less than Mgcos20∘. (3) The fractional change in the time period of a pendulum on changing the temperature is independent of the length of the pendulum.
As the length of a simple pendulum is increased, the maximum velocity of its bob during its oscillation will also decreases.
View SolutionA lift having a simple pendulum attached with its ceiling is moving upward with constant acceleration 'a'. What will be the tension in the string of pendulum with respect to a boy inside the lift and a boy stansing on earth, mass of bob of simple pendulum is m.
View Solution
