A simple pendulum of time period 1s and length l is hung from a fixed support at 0. Such that the bob is at a distance H vertically above A on the ground (figure) the amplitude is $θ_{0}$ the string snaps at $0 = θ_{0} / 2 .$ Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume $θ_{0}$ to be small, so that ${sin θ}_{0} \approx θ_{0} and {cos θ}_{0} \approx 1 .$

Video Solution

Text Solution

Verified by Experts

Consider the diagram.

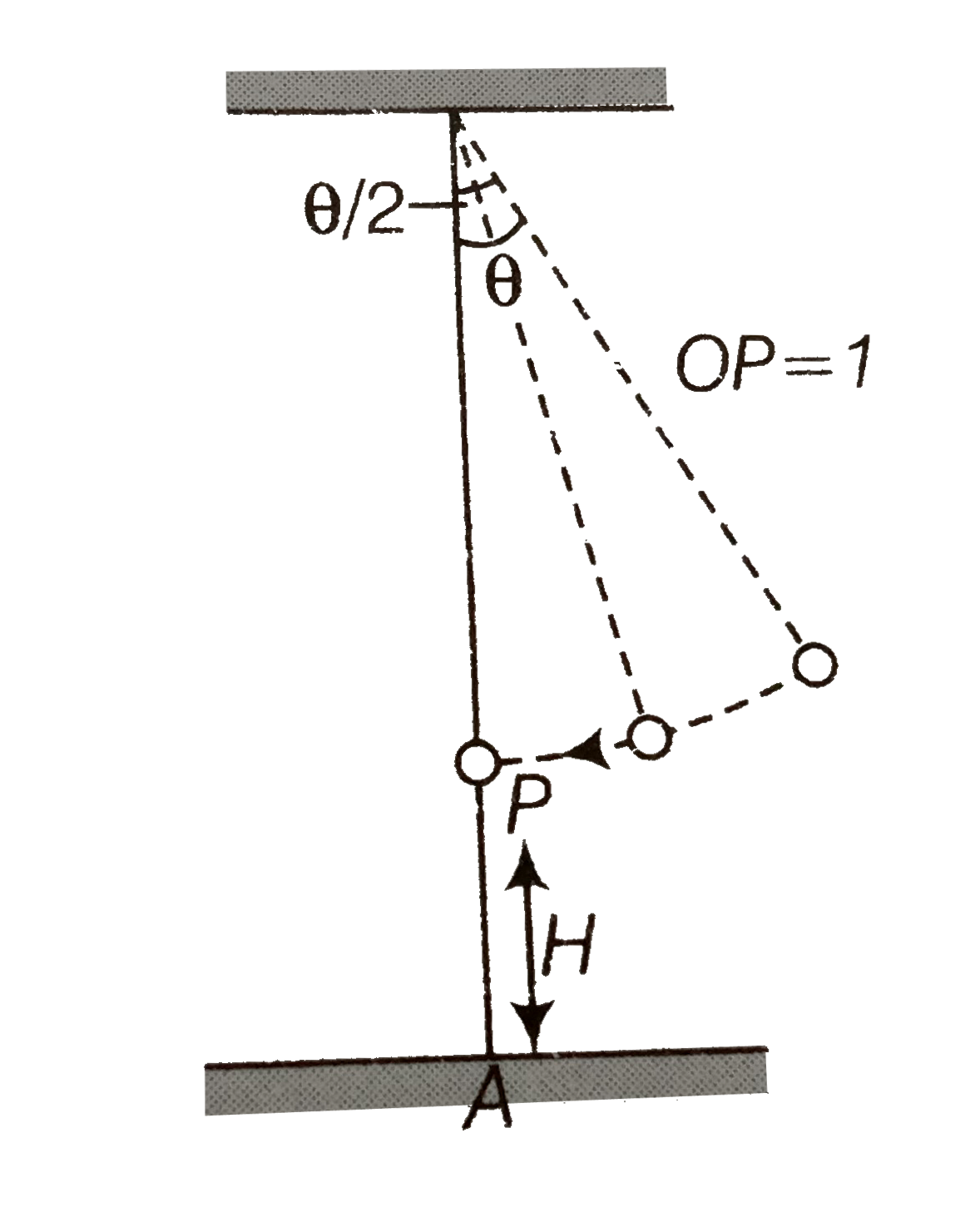
Let us assume $t = 0 when θ = θ_{0} then θ = θ_{0} cos ω t$ Given a seconds pendulum $ω = 2 π \Rightarrow θ = θ_{0} cos 2 π t ... . (i)$
At time $t_{1} let θ = 0_{0} / 2$
$∴ cos 2 π t_{1} = 1 / 2 \Rightarrow t_{1} = \frac{1}{6} [∵ cos 2 π t_{1} = cos \frac{π}{3} \Rightarrow 2 π t_{1} = \frac{π}{3}]$
$\frac{d θ}{d t} = - (θ_{0} 2 π) sin 2 π t [from Eq.(i)]$
At $t = t_{1} = \frac{1}{6}$
$\frac{d θ}{d t} = - θ_{0} 2 π sin . \frac{2 π}{6} = - \sqrt{3} π θ_{0}$
Negative sign shows that it is going left.
Thus, the linear velocity is
$u = - \sqrt{3} π θ_{0} l perperndicular ot the string.$
The vertical component is
$u_{y} = - \sqrt{3} π θ_{0} l sin (θ_{0} / 2)$
and the horizontal component is
$u_{x} = - \sqrt{3} π θ_{0} l cos (θ_{0} / 2)$
At the time it snaps, the vertical height is
$H' = H + l (1 - cos (θ_{0} / 2)) ... . . (i i)$
Let the time required for fall be t, then
$H' = u_{y} t + (1 / 2) {gt}^{2} (notice g also in the negative direction)$
or $\frac{1}{2} {gt}^{2} + \sqrt{3} π θ_{0} l sin \frac{θ_{0}}{2} - H' = 0$
$- \sqrt{3} π θ_{0} l sin \frac{θ_{0}}{2} \pm \sqrt{3 π θ_{0}^{2} l^{2} {sin}^{2} \frac{θ_{0}}{2} + 2 g H'}$
$∴ t = \frac{\sqrt{3} π θ_{0} l sin . \frac{θ_{0}}{2} \pm \sqrt{3 π θ_{0}^{2} l^{2} {sin}^{2} . \frac{θ_{0}}{2}} + 2 g h'}{g}$
$= \frac{\sqrt{3} π l \frac{θ_{0}^{2}}{2} \pm \sqrt{3 π^{2} (\frac{θ_{0}^{4}}{4}) l^{2} + 2 g H'}}{g} [∴ sin . \frac{θ_{0}}{2} = \frac{θ_{0}}{2} for small ange]$
Given that $θ_{0}$ is small, hence neglecting terms ot order $θ_{0}^{2}$ and higher
$t = (\frac{\sqrt{2 H}}{g})$ [from Eq . .. (iii)]
Now $H' \approx H + l (1 - 1) [∴ {cos θ}_{0} / 2 \approx 1]$
$\Rightarrow t = \sqrt{\frac{2 H}{g}}$ [ from Eq. (ii) ]
The distance travelled in the x-direction is u $t x$ to the left of where the bob is snapped
$X = U x = t \sqrt{3} π θ_{0} l Cos (\frac{θ_{0}}{2}) \sqrt{\frac{2 H_{s}}{g}}$
As $θ_{0}$ is small $\Rightarrow cos (\frac{θ_{0}}{2}) \approx 1$ $X = \sqrt{3} π θ_{0} l \sqrt{\frac{6 H}{g}} θ_{0} π l$
At the time of snapping, the bob was a horizontal distance of $l sin (θ_{0} / 2) \approx l \frac{θ_{0}}{2}$ from A
Thus, the distance of bob from A where it meets the ground is
$\frac{l θ_{0}}{2} - X = \frac{l θ_{0}}{2} - \sqrt{\frac{6 H}{g}} θ_{0} l π$
$= θ_{0} l (\frac{1}{2} - π \sqrt{\frac{6 H}{g}})$

Updated on:21/07/2023

A ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
A $\sqrt{2} h / g$
B $\sqrt{8 h / g}$
C $\frac{\sqrt{u^{2} + 2 g h}}{g}$
D $\frac{u}{g} + \frac{\sqrt{2 h}}{g}$
If a simple pendulum of length l has maximum angular displacement $θ$ , then the maximum velocity of the bob is
A $\sqrt{\frac{L}{g}}$
B $2 \sqrt{g} l sin (\frac{θ}{2})$
C $\sqrt{2 g l} sin θ$
D $\sqrt{2 g l}$
A simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle $θ$ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
A $t = 2 π \sqrt{l / g}$
B $t = 2 π \sqrt{l cos θ / g}$
C $T = \frac{4 π^{2} m l}{t^{2}}$
DThe bob is in equilibrium