A tunnel is dug through the centre of the earth. Shwo that a body of mass m when dropped form rest from one end of the tunnel will execute simple harmonic motion.
Consider the situation shown in the diagram.
The gravitational force on the earth in shells internal to the position of the particle.

More clearly,
let g' be the acceleration at P.
So, g'=g(1−dR)=g(R−dR)
From figure, R−d=y
⇒g'=gyR,
Force on body at p, F=−mg'=−mgRy .....(i)
⇒F∝−y [where,y is distance from the centre]
So, motion is SHM.
For time period, we can write Eq. (i)
Asma=−MgRy⇒a=−gRy
Comparing with a=−ω2y
ω2=gR
⇒(2πT)=gR⇒T=2π√Rg
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:NCERT EXEMPLARChapter:MOTION IN A STRAIGHT LINE Exercise:Very Short Answer Type Qns
Explore 14 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NCERT EXEMPLARChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:very short answer type questions
Explore 18 Videos
Similar Questions
Imagine a tunnel dug along a diameter of the earth. Show that a particle dropped from one end of the tunnel executes simple harmonic motion. What is the time period of this motion? Assume the earth to be a sphere of uniform mass density (equal to its known average density=5520 kg m−3.)G=6.67×10−11Nm2kg−2.Neglect all damping forces.
View SolutionA tunnel has been dug through the centre of the earth and a ball is released in it. It executes S.H.M. with time period
View Solution
Knowledge Check
A tunnel has been dug through the centre of the earth and a ball is released in it. It will reach the other end of the tunnel after
A84.6 minB42.3 minC1 dayDWill not reach the other endA tunnel has been dug through the centre of the Earth and a ball is released in it. It will reach the other end of the tunnel after about
Aone dayBone hourC42 minD84 minA hole is drilled along the diameter of the earth and pen is dropped into it. The time taken by it is reach other end of the earth is
A162.2 minB84.6 minC21.2 minD42.3 min
A short , straight and frictinless tunnel is bored through the centre of the earth and a body is realesed from the surface into the tunnel . Show that the motion of the body in the tunnell will be simple harmoic and hence calculate the taken by the body to travel from one end of the tunnel to the other (Radius of the earth = 6.38×106m and acceleration due to gravity at the surface = 9.81ms2
View SolutionAsume that as narrow tunnel is dug between two diametricaly opposite points of the earth. Treat the earth as a solid sphere of uniform density. Show that ilf a particle is relesed in this tunel, ilt wil execute a simple harmonic motion. Calculate the time period of this motion.
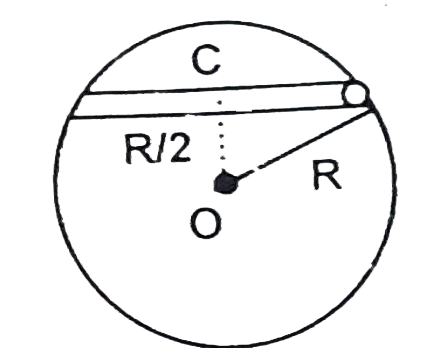
View SolutionAssume that a tunnel is dug along a chord of the earth, at a perpendicular distance (R/2) from the earth's centre, where 'R' is the radius of the Earth. The wall of the tunnel is frictionless. If a particle is released in this tunnel, it will execute a simple harmonic motion with a time period :
View SolutionA tunnel has been dug through the centre of the earth and a ball is released in it. It executes S.H.M. with time period
View SolutionA tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
View Solution